变幅多轴疲劳寿命分析方法对比

刘天奇， 时新红,*， 张建宇， 费斌军

(1. 北京航空航天大学 航空科学与工程学院, 北京 100083； 2. 重庆大学 航空航天学院, 重庆 400044)

在工程实际中，对于承受疲劳载荷的结构件，其危险部位往往处于多轴疲劳应力(应变)状态。多轴疲劳是指多向应力或应变作用下的疲劳，也称复合疲劳。多轴疲劳损伤发生在多轴循环加载条件下，加载过程中有多个应力(应变)分量独立地随时间发生周期性变化。这些应力(应变)分量的变化可以是同相位、呈比例的，也可以是非同相、非比例的[1]。

早期对于多轴疲劳的研究主要针对恒幅加载，并提出了许多比较有效的多轴疲劳寿命预测模型[2-4]。近些年来，变幅载荷下的多轴疲劳研究取得了较大的进展[5-8]，并对其工程应用也开展了一些研究[9-12]。变幅多轴疲劳寿命分析方法一般包含循环计数法、疲劳损伤模型及累积损伤准则，其中循环计数法和疲劳损伤模型是变幅多轴疲劳寿命分析方法的核心问题。单轴变幅疲劳中通常采用雨流计数法[13]将复杂载荷处理为简单载荷，并结合应力(应变)-寿命曲线进行损伤计算。在多轴变幅载荷下，各应力(应变)分量均会对疲劳损伤产生影响，而应力(应变)主轴随时间不断变化导致损伤的确定更加困难[1,4-5]。此外，多个应力(应变)分量之间存在相位差导致峰谷值不同时出现，使得循环计数方法更加复杂。对此，不同的学者提出了不同的寿命预测方法，如积分法[14]、能量法[15]、增量损伤法[16]和临界平面法等，其中临界平面法是分析多轴疲劳寿命较为有效的方法。Socie[4]、Bannantine[17]等提出对不同平面上的应力(应变)-时间历程进行循环计数，并将承受最大损伤的平面作为临界面，采用修正的Smith-Watson-Topper损伤模型进行损伤计算，该方法临界面的确定需要对所有可能失效的平面进行损伤计算。Wang和Brown[18-19]提出了一个基于等效应变的循环计数法，根据等效应变-时间历程依次计数，并提出了相应的损伤模型，该方法采用等效应变计数，在某种程度上造成了应力应变符号的丢失。Shang和Wang等[20]以临界面上的剪应变为主计数通道，采用雨流计数法进行循环计数，根据得到的剪应变全循环，取该全循环下最大剪应变折返点之间的正应变的变化范围作为一对循环计数结果。此外，Shang和Wang[21]提出了一种统一型多轴疲劳损伤模型进行损伤计算。王雷-王德俊方法[22-23]同样以临界面上的剪应变为主计数通道，在得到剪应变循环后，取每个剪应变全循环对应的正应变最大变程，以此作为一对计数结果，但王雷和王德俊未提出相应的疲劳损伤模型，而是使用了Shang-Wang提出的统一型多轴疲劳损伤模型[23]，该方法对316L不锈钢的预测结果偏保守。此外，还有许多基于临界面法的寿命分析方法的提出[5,20,24]。如包名等[24]基于von Mises等效应变等效应力概念、符号修正公式以及传统的单轴雨流计数法提出了一种多轴随机载荷下的循环计数法；Meggiolaro[25]、Chen和Shang[26]等都对Wang-Brown方法进行了修正。目前工程中应用较为广泛的主要是Bannantine-Socie方法和Wang-Brown方法。

本文对3种基于临界平面法的变幅多轴疲劳寿命分析方法进行了编程实现，并针对飞机上某结构危险部位的应力(应变)-时间历程，采用3种多轴疲劳寿命分析方法和单轴的Manson-Coffin方程[13]进行了寿命分析。对预测结果进行对比分析，研究变幅多轴疲劳寿命分析方法在飞机结构中的适用性。

1 变幅多轴疲劳寿命分析方法

变幅多轴疲劳寿命分析方法一般包含3个步骤：首先进行多轴载荷下的循环计数，将复杂载荷简化为简单的循环载荷；其次采用疲劳损伤模型对每个循环进行疲劳损伤计算；最后基于累积损伤理论对多轴疲劳寿命进行预测[4]。其中循环计数法和疲劳损伤模型是变幅多轴疲劳寿命分析方法的核心问题。

1.1 Bannantine-Socie方法

Bannantine-Socie方法是一种比较早的方法，其包含循环计数法和疲劳损伤模型2个部分。其中循环计数法是基于临界面原理提出的一种计数方法。该计数方法认为疲劳破坏发生在最大损伤平面上，并将最大损伤平面作为临界面，计算临界面上的应变-时间历程，采用雨流计数法对该平面上的应变进行循环计数，得到简单循环。疲劳损伤模型由Smith-Watson-Topper损伤模型推广得到，提出以最大正应变幅平面上的正应变变程和当前循环中的最大法向应力的乘积作为多轴疲劳损伤参量，所建立的多轴疲劳损伤模型为

(1)

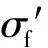
1.2 Wang-Brown方法

Wang-Brown方法同样包含循环计数法和疲劳损伤模型两部分。其中循环计数法基于相对等效应变的概念，因此也称为相对等效应变计数法。通过该方法，可将随机加载的多轴应变-时间历程折合成一个相对等效应变的时间历程，之后对该相对等效应变进行计数。基本步骤如下：

1) 对于多轴疲劳加载应变历程εij(t)、应力历程σij(t)，计算von Mises等效应变εeq(t)为

(2)

式中：ν′为有效泊松比；ε11、ε22和ε33为3个正应变大小；γ12、γ13和γ23为3个切应变大小。

(3)

记录此时相对等效应变由0点到最高点所对应的加载历程起始点和终止点为一个循环。

3) 对剩下的等效应变-时间历程重复上述步骤，直到记录下所有的循环为止。

Wang-Brown方法根据所提出的多轴循环计数方法，提出寿命预测模型：

(4)

式中：Δγmax为一个加载历程中的剪应变增量；Δεn为从起点至终点的连续历程区间中最大剪应变平面上的正应变变化量；S为材料常数(钢材料通常取1.5～2.0，对于6061-T6铝合金材料[27]其值约为1.0)，可由多轴疲劳试验测得；σn,mean为最大剪应变平面上的平均法向应力。

1.3 王雷-王德俊方法

王雷和王德俊[22-23]提出了一种多轴循环计数法，采用统一型多轴疲劳损伤模型进行损伤折算。王雷和王德俊[22-23]所提出的循环计数法基于临界平面法，认为多轴疲劳破坏的主要原因是临界剪切面上的交变剪应力，同时垂直于该平面的正应力对疲劳损伤也有贡献。该循环计数法认为剪应变2个半循环的物理意义相同，不区分加载半循环和卸载半循环，其处理过程主要为根据某点的应变-时间历程计算临界平面上的剪应变、正应变时间历程，对剪应变进行雨流法循环计数，对应得到剪应变的全循环和折返点信息，提取每个全循环中剪应变折返点对应的正应变最大变程，以此作为一次循环计数。

临界面采用权值平均最大剪应变平面为临界面，该临界面的确定如下：

1) 对于最大剪应变序列中的有效峰值点γmax(ti)，其所在平面的法向单位向量为pi。

2) 利用式(5)计算权值。

(5)

式中：τ-1为剪切疲劳极限；G为剪切模量；Di为相应剪应变下的损伤值(采用Manson-Coffin方程计算)；k可以取0.3。对应的该时刻的加权值，用矢量来表示为

w(ti)=wipi

(6)

可以看到在权值计算公式中，忽略了较小的剪应变值造成的损伤。

3) 对于计算得到各时刻的加权矢量进行叠加，最终得到的方向矢量单位化即为临界平面的法方向。

(7)

王雷-王德俊方法未提出相应的多轴疲劳损伤模型，采用Shang和Wang提出的统一性多轴疲劳损伤模型[21]进行损伤计算。该模型提出一个与加载路径无关的多轴疲劳损伤参量(式(8))，基于该损伤参量，提出的寿命预测模型如式(9)所示。

(8)

(9)

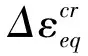
对于以上3类变幅多轴疲劳寿命分析方法，得到各循环的损伤后采用Minner线性累积损伤准则进行最终的寿命预测。

2 寿命预测分析

2.1 编程实现

对于第1节中的3种变幅多轴疲劳寿命分析方法，主要包括5个步骤：

1) 确定临界面。

2) 计算临界面上的应变-时间历程。

3) 对应变-时间历程循环计数。

4) 计算每个循环下的损伤。

5) 采用累积损伤准则计算最终的疲劳寿命。

在编程实现过程中，临界面的确定和循环计数法是核心问题。而循环计数法的核心即雨流计数法，计数法的流程参照文献[9]中的流程进行编程，此处不再赘述。

3种方法中，Bannantine-Socie方法需要计算临界面上的正应变和正应力；Wang-Brown方法需要计算最大剪应变，正应变及正应力；王雷-王德俊方法需要计算应变-时间历程中的最大剪应变值及其方向。

Bannantine-Socie方法需要通过计算所有平面上的损伤来确定最大损伤面。在三维直角坐标体系下，任意平面的法向向量与3个坐标轴的夹角分别为θ、φ及ξ，则该平面的单位法向向量为

l=(cosθ,cosφ,cosξ)

(10)

根据几何关系可知：

(11)

对于给定的某点的三向应变状态εij，在该点处任意平面上的正应变为

εn=lεijlT

(12)

因此，处于三向应变状态的某点处任意方向平面上正应变都可以由2个参数θ、φ来确定，且θ、φ的变化范围为0～π。可以由向量l确定平面方向后，计算该方向上的应变、应力时间历程，进行循环计数，并计算损伤。Bannantine-Socie方法流程如图1所示，对θ、φ每隔5°进行一次计算，共得到1 296个平面上的损伤值，取所有平面中最大的损伤值作为最终的预测结果。图1中θ或φ每增加5°则i的值加1，因此不同的i值对应不同的平面方向，D(i)表示该平面上的损伤。

Wang-Brown方法基于等效应变计数，对于一对计数结果，需要计算最大剪应变变程所在的平面。然而在变幅多轴加载历程中，任意平面上的剪应变历程大小和方向都发生变化。因此，需要分别计算任意平面上所有方向的剪应变，确定最大的剪应变变程。对于一点处任意平面，假设其方向为l，建立直角坐标系，设单位向量n2，n3位于该平面上且互相垂直，如图2所示。

对于该平面上任意方向的单位向量可以由式(13)表示，由l和m即可计算得到该平面上与向量m方向一致的剪应变，变换α的值即可计算任意方向上的剪应变γn，如式(14)所示。

m=n2cosα+n3sinα

(13)

γn=2n1εijmT

(14)

Wang-Brown方法对于一对计数结果，其造成的损伤计算流程图如图3所示，同样θ、φ以5°作为增量。在图3中，θ每增加5°则i的值加1，φ每增加5°则j的值加1。对于一个固定的平面(θ，φ不变)，需要计算该平面上最大剪应变，α每增加5°则k的值加1。以D(i,j,k)表示每次计算得到的损伤，最后取D(i,j,k)中最大值作为最终的损伤值。

王雷-王德俊方法临界面的确定需要计算最大剪应变平面的方向。对于三维应变状态下的最大剪应变采用如下公式计算：

图3 Wang-Brown方法流程图Fig.3 Flowchart of Wang-Brown method

γmax=ε1-ε3

(15)

式中：ε1和ε3分别为第一主应变和第三主应变。主应变采用特征方程求解：

|εij-λδij|=0

(16)

其中：δij为单位矩阵;λ为特征值。式(16)对应的3个特征值即为3个主应变，3个特征向量为3个主应变的方向。设3个主应变ε1>ε2>ε3对应的方向向量分别为q1、q2和q3，则最大剪应变平面方向的单位向量r可以表示为

(17)

通过计算最大剪应变值及其方向，可以得到权值最大平均应变平面，确定王雷-王德俊方法的临界面方向，之后同样采用式(13)、式(14)对临界面上任意方向的剪应变历程进行计算，循环计数并确定损伤最大的方向。王雷-王德俊方法流程图如图4所示，α每增加5°则i的值加1，D(i)表示对应不同i值的损伤，共计算36次损伤，取损伤最大的方向作为最终预测结果。

2.2 算 例

飞机某结构在飞机服役过程中承受着随机载荷作用。该结构设计使用材料为7B04铝合金材料，其基本力学性能如表1所示，其中σ0.2为屈服极限，σu为强度极限，ν为泊松比。

对于一个起落，载荷施加顺序为：着陆起转、着陆回弹、着陆振荡、第2次着陆撞击、着陆滑跑、中等刹车、最大刹车、着陆曲线滑行、转弯、牵引、起飞曲线滑行、发动机试车及起飞滑跑。该结构的设计载荷谱按着陆轻重程度的不同分为A、B、C和D 4个类型，以20个起落为一个加载循环谱块，对应20个飞行小时，载荷谱的排列顺序如表2所示。

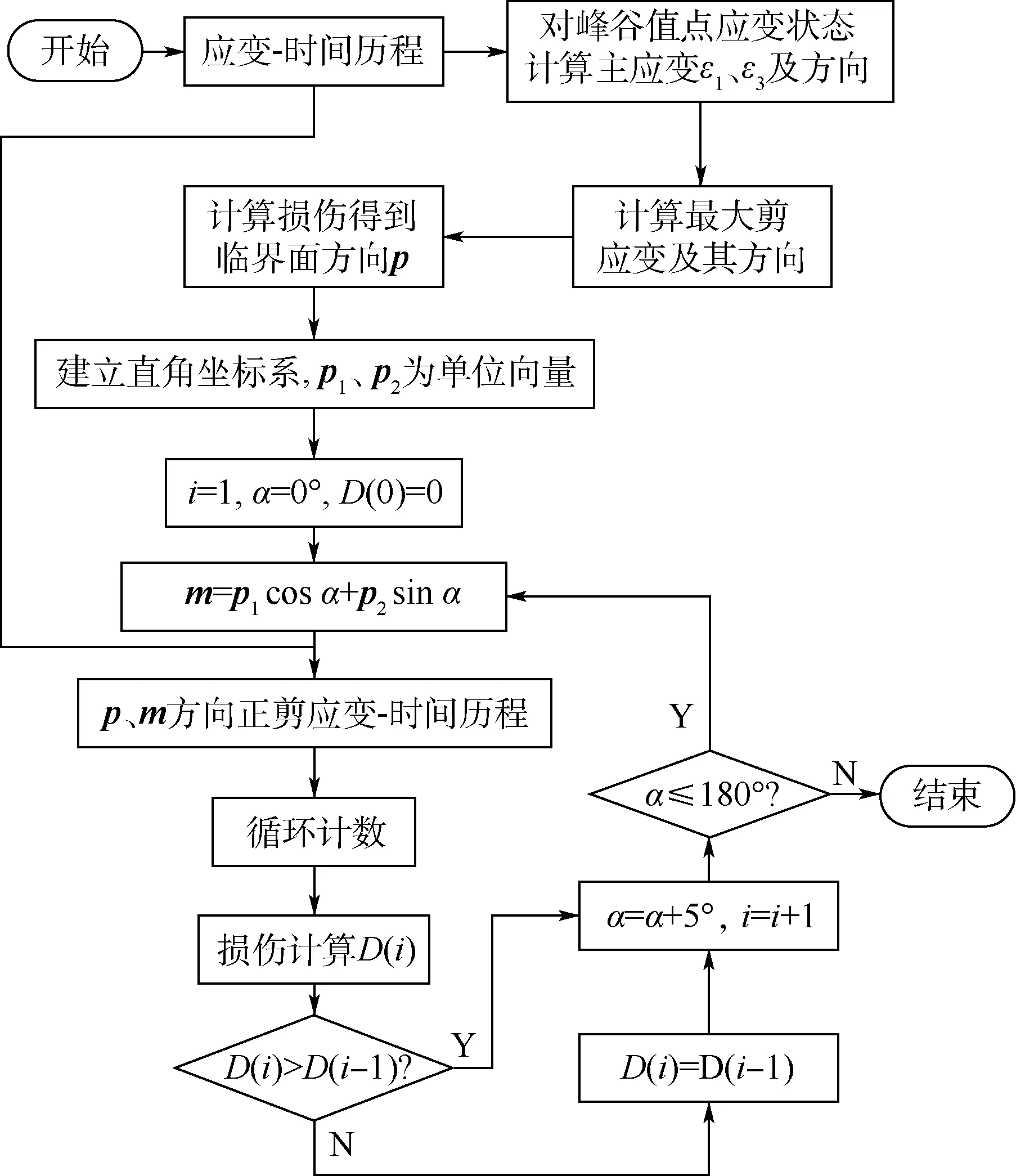
图4 王雷-王德俊方法流程图Fig.4 Flowchart of Wang L-Wang D J method

力学性能数 值E/GPa 70σ0.2/MPa449σu/MPa490ν0.3σ′f/MPa916b-0.0803ε′f0.2316c-0.8734

对该结构进行有限元分析，得到该结构危险部位如图5所示。对于不同类型的起落，该危险部位的6个应变分量及应力分量的时间历程如图6、图7所示。其中：s11、s22、s33分别为3个正应力分量大小；s12、s23、s13分别为3个切应力分量大小。

分别采用上述3种变幅多轴疲劳寿命分析方法对该结构危险部位进行寿命预测。同时，为了比较多轴载荷对结构件疲劳寿命的影响，采用单轴低周疲劳的Manson-Coffin方程对结构件进行寿命预测。Manson-Coffin方程描述应变-寿命曲线的公式为

(18)

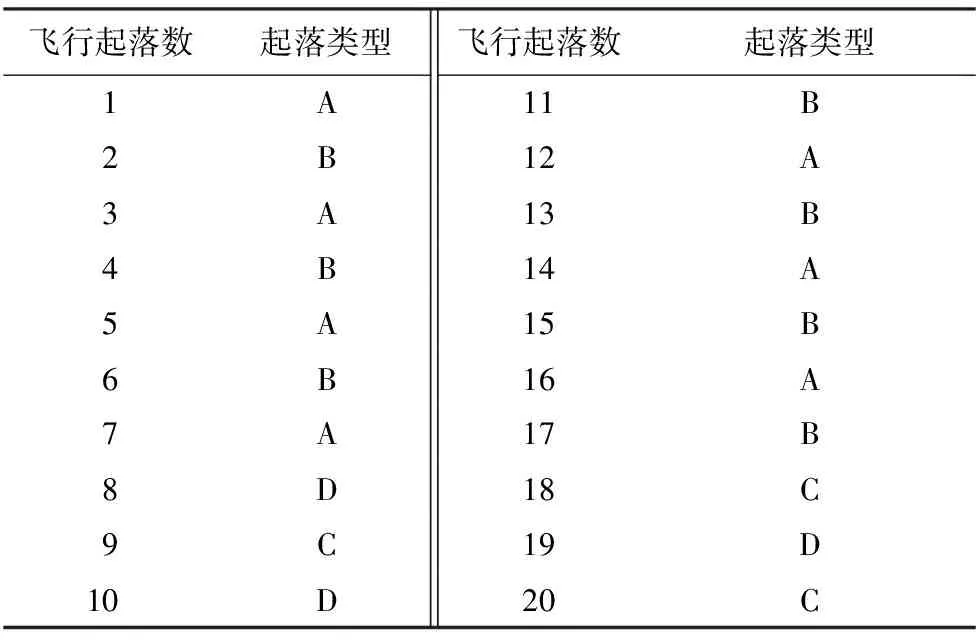
表2 飞机某结构危险部位载荷谱排列顺序

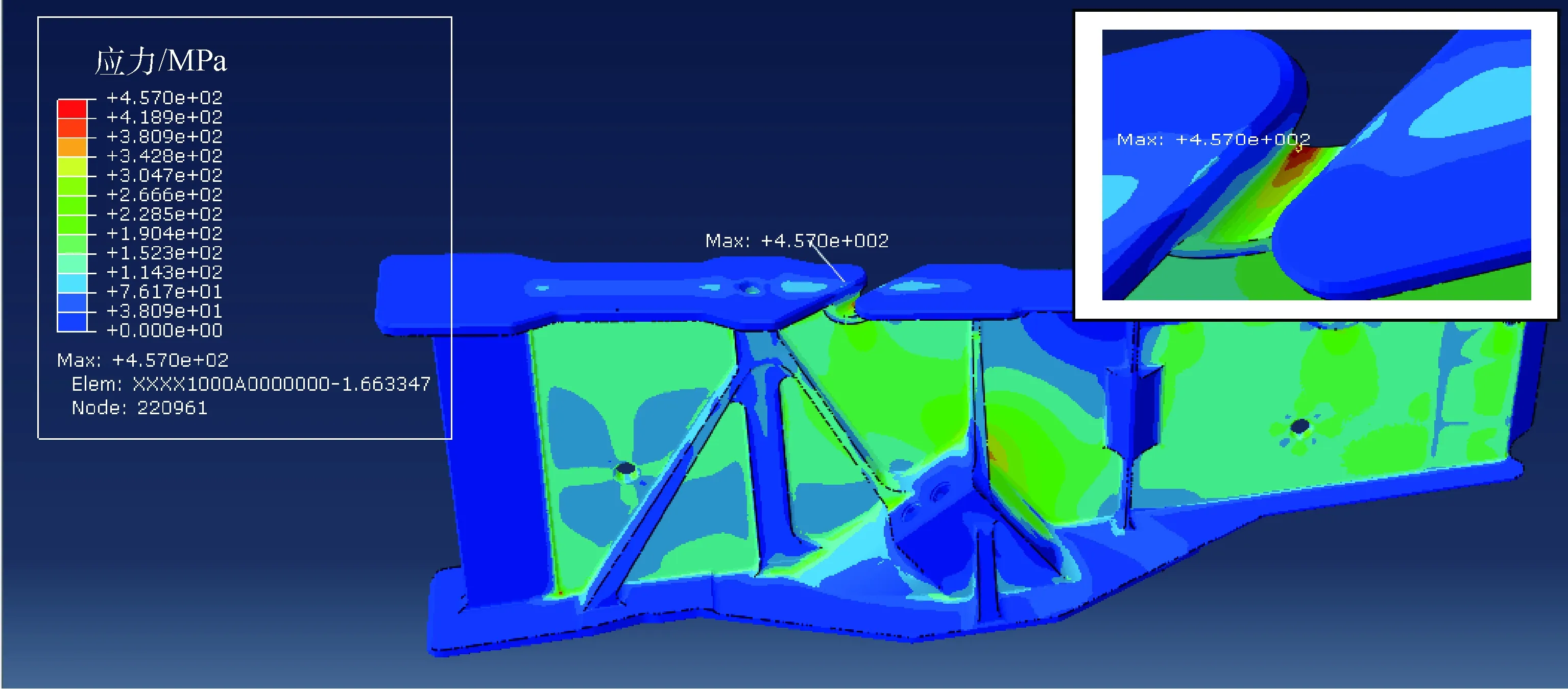
图5 结构的应力云图及危险部位Fig.5 Stress contour and critical site of structure

图6 飞机某结构危险部位承受的应变-时间历程Fig.6 Strain-time history of an aircraft structure’s dangerous part

图7 飞机某结构危险部位承受的应力-时间历程Fig.7 Stress-time history of an aircraft structure’s dangerous part

使用Manson-Coffin方程进行寿命预测时，针对结构危险部位的应变-时间历程编程实现，主要分以下4个步骤：

1) 分别计算不同平面上的正应变时间历程，平面方向同样由包含θ、φ的向量表示。

2) 对所有平面上的正应变时间历程进行雨流计数得到各平面上的正应变循环。

3) 采用Manson-Coffin方程分别对所有平面上每个循环进行损伤计算，采用Minner线性累积损伤准则计算每个平面的寿命。

4) 取所有平面中最短的寿命为最终的寿命预测结果。

4种不同的寿命预测方法的预测结果如表3所示。

文献[28]中给出了歼8Ⅰ型、歼8Ⅱ型及歼8白天型飞机结构相关部位的首翻期大约是1 500～1 800飞行起落，修理间隔为1 350～1 500飞行起落，总寿命约3 900～4 500飞行起落。

若以歼8各型号飞机相关部位的首翻期寿命为参照，Wang-Brown方法中当系数S取1.0～1.5之间时，寿命预测结果较为合理；王雷-王德俊方法的预测结果则会偏于保守；而Bannantine-Socie方法预测结果较其他2种方法偏大，这是因为该方法虽然以最大损伤平面作为临界面，但其损伤模型形式导致在最大损伤平面上其忽略了剪应变对疲劳损伤的影响。此外，若采用单轴疲劳寿命分析方法(Manson-Coffin方程)来预测承受多轴载荷的结构件，计算得到的疲劳破坏寿命远大于多轴计算模型所预测的结果。

表3 各方法疲劳寿命预测结果

3 结 论

针对常用的3种变幅多轴疲劳寿命预测方法进行编程实现，并通过对承受多轴疲劳载荷的飞机某结构危险部位进行寿命预测发现：

1) 采用单轴疲劳寿命分析方法(Manson-Coffin方程)对其进行寿命分析会有较大的误差。

2) Wang-Brown方法中,当系数S取1.0～1.5之间时，寿命预测结果较为合理；王雷-王德俊方法的预测结果则会偏于保守；而Bannantine-Socie方法预测结果较其他2种模型偏大。

3) Bannantine-Socie方法预测结果之所以偏大是因为较其他2种方法，该方法忽略了某些循环存在的剪应变对疲劳损伤的影响，导致预测结果偏大。