卷绕机锭轴的O型橡胶圈柔性支承系统动力学参数测试与分析

李 仲， 甘学辉， 刘国志， 马勋勋， 王生泽， 1b， 王永兴

(1.东华大学 a.机械工程学院； b. 纺织装备教育部工程研究中心， 上海 201620； 2. 郑州华萦化纤科技有限责任公司， 河南 郑州 450001)

高速卷绕机是涤纶长丝生产过程中的重要设备，锭轴转子系统是高速卷绕机的核心部件，掌握卷绕机锭轴转子动力学行为特点及机理，对研发具有自主知识产权并满足化纤生产市场需求的高速卷绕机具有重要意义[1]。锭轴转子系统采用的O型橡胶圈柔性支承结构，可有效调节系统动态特性，从而提高锭轴工作的稳定性[2-5]。合理选择和优化O型橡胶圈柔性支承系统的刚度和阻尼参数值是设计涤纶长丝卷绕机锭轴结构和参数的基础。

橡胶是典型的黏弹性材料，由于其在宽广的频域范围内能起阻尼减振作用，作为隔振元件被广泛应用。另外，由于橡胶阻尼器有较宽的阻尼和刚度选择范围，因此在旋转机械中也得到了广泛的应用。

当橡胶作为阻尼元件使用并受到动态载荷时，具有较强的非线性特征，其阻尼特性与动载荷的激振频率和振幅相关，因此，研究人员采用不同的模型，如Maxwell模型、Kelvin-Voigt模型以及分数导数模型来表征橡胶隔振器动态特性的频率相关性[6-10]。除了动载荷的频率和幅值，其他因素也会影响橡胶阻尼元件的动态性能。韩德宝等[11]研究表明，橡胶隔振器的性能随着材料、温度等很多因素的变化而变化。

O型橡胶圈除了可用作阻尼元件外，也常被用作弹性支承的支承件。Powell等[12]对O型橡胶圈支承的气体轴承进行了研究。Kazimierski[13]通过理论和试验研究证明，带弹性O型橡胶圈支承的静压气体轴承能够提高转子的稳定速度。尹佩琪[14]提出了一种O型胶圈支承空气轴承失稳速度的简化理论计算方法。宣海军等[4]证实O型橡胶圈用作弹性支承的支承件，其能有效地抑制高速转子系统的不平衡响应并且可以提高系统稳定性。所有这些研究为O型橡胶圈作为支承件奠定了基础。

由于受到多种非线性因素的影响，目前还没有一种理论模型能够全面地反映这些因素对于橡胶圈支承件性能的影响，所以大部分对橡胶圈支承件动态性能的研究采用试验测试的方法[15]。文献[16]通过试验方法——基础激振共振质量法，得到了较为全面的橡胶材料动力学参数测试数据。Smalley等[17]采用同样的方法对O型橡胶圈的动态性能进行了测试，得到了温度、激振幅值、材料、压缩、拉伸、橡胶环截面直径等参数对动态特性的影响。尹佩琪[18]首次采用基础激振共振质量法对用在气体轴承上的3种不同O型橡胶圈刚度、阻尼系数进行了测试，同时考察了供气和O型橡胶圈安装压缩量对刚度和阻尼系数的影响。吴荣仁[19]利用Kelvin-Voigt黏弹性力学模型，对丁腈橡胶O型橡胶圈在400～1500 Hz激振频率下进行了测试。王成林[20]利用基础激振共振质量法对O型橡胶圈的动态特性进行了测试，得到了在100～1 600 Hz之间橡胶圈动力学参数与频率的对应关系。苏小雯[21]对橡胶圈参数与其频变特性关系展开试验研究，测试的频率范围为60～150 Hz，测得的不同激振频率的试验数据为进一步计算分析含有橡胶圈支承的转子系统动力学行为奠定了基础。

不同型号设备的卷绕机锭轴根据结构参数和工艺不同而采用不同几何参数和数量的橡胶圈。另外由于卷绕锭轴是在较为宽广的频率范围内工作，并且由橡胶圈构成的柔性支承系统动力学参数呈现非线性和频变特性，造成橡胶圈柔性支承系统动力学参数值具有较强的个性化。为了更好地分析研究ZWT 612-180型卷绕机的锭轴转子动态特性，需准确得到锭轴结构中含不同几何参数O型橡胶圈支承系统的动力学参数值及频变规律。本文依照ZWT 612-180型卷绕机锭轴的柔性支承结构参数进行测试模型设计，运用受迫非共振法，在其工作频率范围内研究具有不同外形结构参数的橡胶圈以及橡胶圈数量对柔性支承系统动力学参数频变特性的影响，通过测试得到O型橡胶圈柔性支承系统的刚度系数与阻尼系数以及其随频率变化的规律，并运用Matlab拟合出其动力学参数频变特性曲线，并给出相应计算公式，为进一步分析和优化设计含有柔性支承系统的锭轴卷绕转子结构打下基础。

1 卷绕机锭轴结构及工作状态

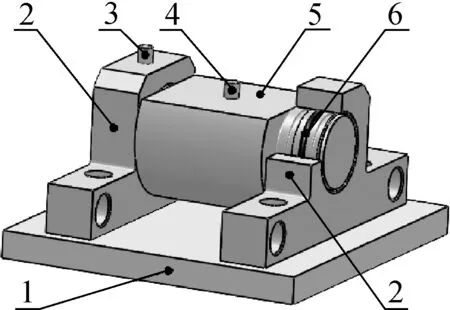
ZWT 612-180型卷绕机锭轴结构原理如图1所示，其主要由支撑臂(1)、转轴(6)、夹套(10)、过渡套(2、 4、 8)通过含橡胶圈(11、 12、 13、 14)的柔性支承和滚动轴承(3、 5、 7、 9)装配而成。该卷绕机锭轴采用4种不同规格的橡胶圈，橡胶圈规格参数和数量不同，安装设计结构类似。卷绕机锭轴上橡胶圈的安装结构如图2所示。O型橡胶圈被预压缩安装在沟槽中，周围存满油脂，由滚动轴承、橡胶圈、油脂等构成柔性支承系统。

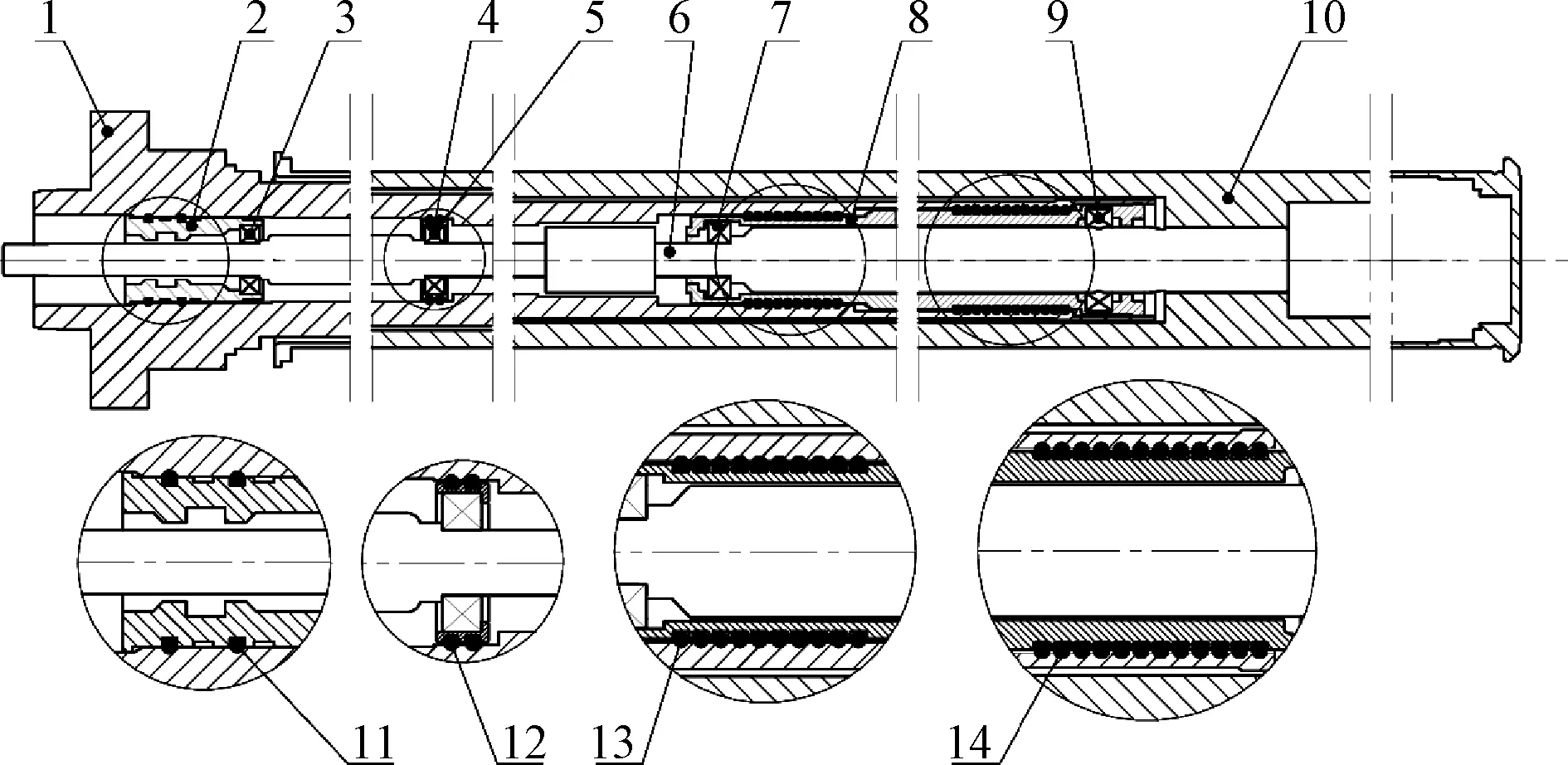
1—支撑臂； 2—过渡套Ⅰ； 3—滚动轴承Ⅰ； 4—过渡套Ⅱ； 5—滚动轴承Ⅱ；6—转轴； 7—滚动轴承Ⅲ； 8—过渡套Ⅲ； 9—滚动轴承Ⅳ； 10—夹套；11—橡胶圈Ⅰ； 12.—橡胶圈Ⅱ； 13—橡胶圈Ⅲ； 14—橡胶圈Ⅳ图1 ZWT 612-180型卷绕机锭轴结构原理图Fig.1 Spindle structure principle diagram of ZWT 612-180 winding machine

1—滚动轴承； 2—橡胶圈； 3—支撑臂； 4—转轴； 5—过渡套图2 O型橡胶圈安装结构Fig.2 Elastomer O-ring mounting structure

目前，涤纶长丝卷绕机的卷绕线速度一般为3 000～5 000 m/min，本文所分析的ZWT 612-180型卷绕机的卷绕线速度为4 000 m/min，对应卷绕初始直径为140 mm，最高转速为9 095 r/min(151.6 Hz)，对应卷装最大直径440 mm(满卷状态)时的最低卷绕转速为2 895 r/min(48.3 Hz)。考虑到在频率50 Hz以下时试验振动不稳定，本文将测试50～150 Hz频率范围内4种规格橡胶圈柔性支承系统的动力学参数。

2 理论基础

通过试验测试橡胶圈柔性支承系统动力学参数的方法主要有受迫共振法、受迫非共振法等[9]。由于受迫非共振法不需要更换试验中的振动质量就可计算动力学参数，试验成本相对较低且操作更可靠，本文将采用该方法来进行橡胶圈柔性支承系统动力学参数的测试。单自由度系统受迫振动模型如图3所示。

图3 单自由度系统受迫振动模型Fig.3 Forced vibration model of single degree of freedom system

对振动质量m进行受力分析，考虑系统响应的频变特性，得到单自由度系统动力学方程为

(1)

设系统基础受简谐振动激励y=a0sinωt，振动质量m的响应y1的表达式如式(2)所示。

(2)

式中：a0为简谐位移激励振幅值；a1(ω)为振动质量m的位移响应幅值；ω为激振角频率。

将式(2)代入振动质量m的动力学方程式(1)中，并且使其实部和虚部均为0，则得到式(3)。

(3)

式中：α(ω)=a1(ω)/a0。

因此，当已知系统的振动质量m，激振角频率ω，振动质量m的加速度响应幅值与地基的加速度响应幅值之比α(ω)和两加速度响应的相位差φ，则可计算出单自由度系统的刚度系数k(ω)和阻尼系数c(ω)。

3 试验测试系统

3.1 试验模型及参数

橡胶圈柔性支承系统试验模型的结构如图4所示，振动质量m两端加工有左右对称布置的沟槽，以放置橡胶圈，安装尺寸完全按照实际卡盘轴设计尺寸，放置橡胶圈的沟槽间隙处涂以润滑脂，以确保试验测试数据尽可能符合实际工况。激振台位移振幅满足支承座孔与参振轴无碰撞，并在轴身上部铣出一个平面使其重心在轴线的下方，保证振动质量m做上下振动。

1—底板；2—支承座；3—控制点；4—检测点；5—振动质量m;6—O型橡胶圈图4 O型橡胶圈柔性支承系统试验模型结构图Fig.4 Experimental model structure of elastomer O-ring flexible support system

ZWT 612-180型卷绕机锭轴上所采用的4种不同规格的橡胶圈结构参数如表1所示。

表1 ZWT 612-180型卷绕机柔性支承中橡胶圈结构配置

其中，激振设备通过控制点(3)控制底板(1)，确保支承座(2)输入位移激振幅值a0、激振角频率为ω的正弦激励y。通过控制点(3)和检测点(4)分别得到支承座2和振动质量m的加速度响应值。

3.2 测试系统的组成

依据受迫非共振法测试原理和方法，设计O型橡胶圈柔性支承系统动力学参数的测试系统如图5所示。

本文选择苏州苏试试验仪器股份有限公司生产的DC 3200-36型电动式振动试验台，其正常工作频率范围为5～2500 Hz，额定推力为32 kN，最大加速度达980 m/s2，可满足本文测试需求。

根据试验参数选择2106C型压电式加速度计，其加速度测量范围为3.15～315.00 m/s2，数据采集控制仪至少有2个通道控制加速度，在满足采样定理的情况下，设置不同的采样频率进行正弦激振驻留。振动台位移振幅取0.05 mm，根据工作频率，在不同的激振频率下进行正弦激振驻留，分别得到每个激振频率下振动质量m和支承座的稳态加速度响应。根据试验原理选择数据处理方法，通过数字滤波及相关性分析，计算控制与检测简谐信号的幅值比α(ω)与相位差φ。

由上述装配参数确定橡胶圈柔性支承系统动力学参数的实际测试系统和实际测试模型如图6所示。通过测试系统采集平稳信号，利用自相关分析得到控制与检测加速度响应信号的幅值，利用互相关分析得到控制与检测信号的相位差值，从而得到每个激振频率下O型橡胶圈支承件的刚度系数值和阻尼系数值。

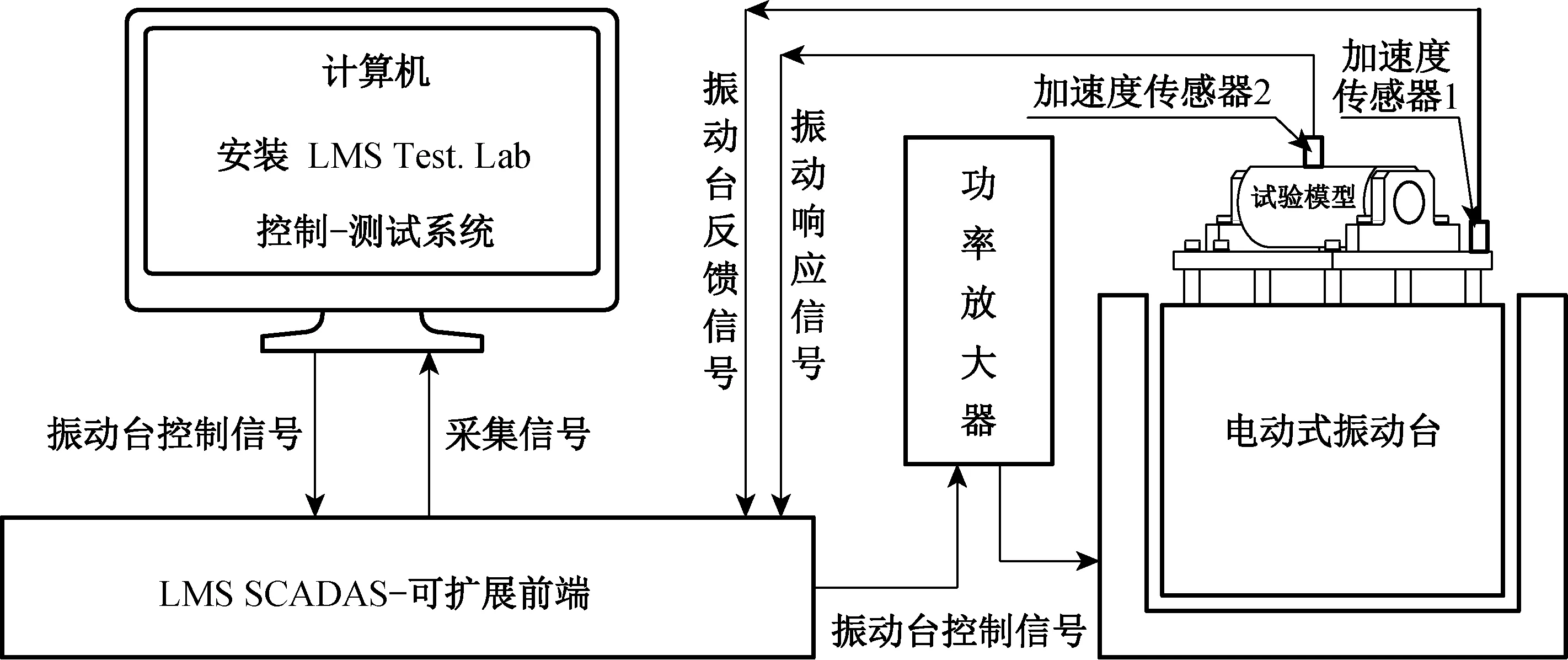
图5 O型橡胶圈柔性支承系统动力学参数的测试系统组成Fig.5 Composition of test system for the dynamic parameters of elastomer O-ring flexible support system

(a) 测试系统

(b) 测试模型 图6 橡胶圈柔性支承系统动力学参数的实际测试系统和测试模型Fig.6 Actual test system and test model for the dynamic parameters of elastomer O-ring flexible support system

4 动力学参数测试及分析

4.1 测试数据

为了更好地分析橡胶圈数量与激振频率对整个柔性支承系统动力学参数的影响，调整橡胶圈数量与激振频率，对模型Ⅰ在18组不同激振频率下含2个φ44、 4个φ44或6个φ44橡胶圈的柔性支承系统进行测试。根据上述试验方法，测得控制点(3)和检测点(4)的加速度信号，通过数字信号处理获得每个激振频率下控制与检测信号的加速度响应幅值和相位差。其中，每个试验频率f对应一个编号i(i=1， 2， …， 18)。模型Ⅰ中O型橡胶圈数量分别为2、4和6个时支承座和振动质量m的加速度响应幅值测试结果如图7所示。

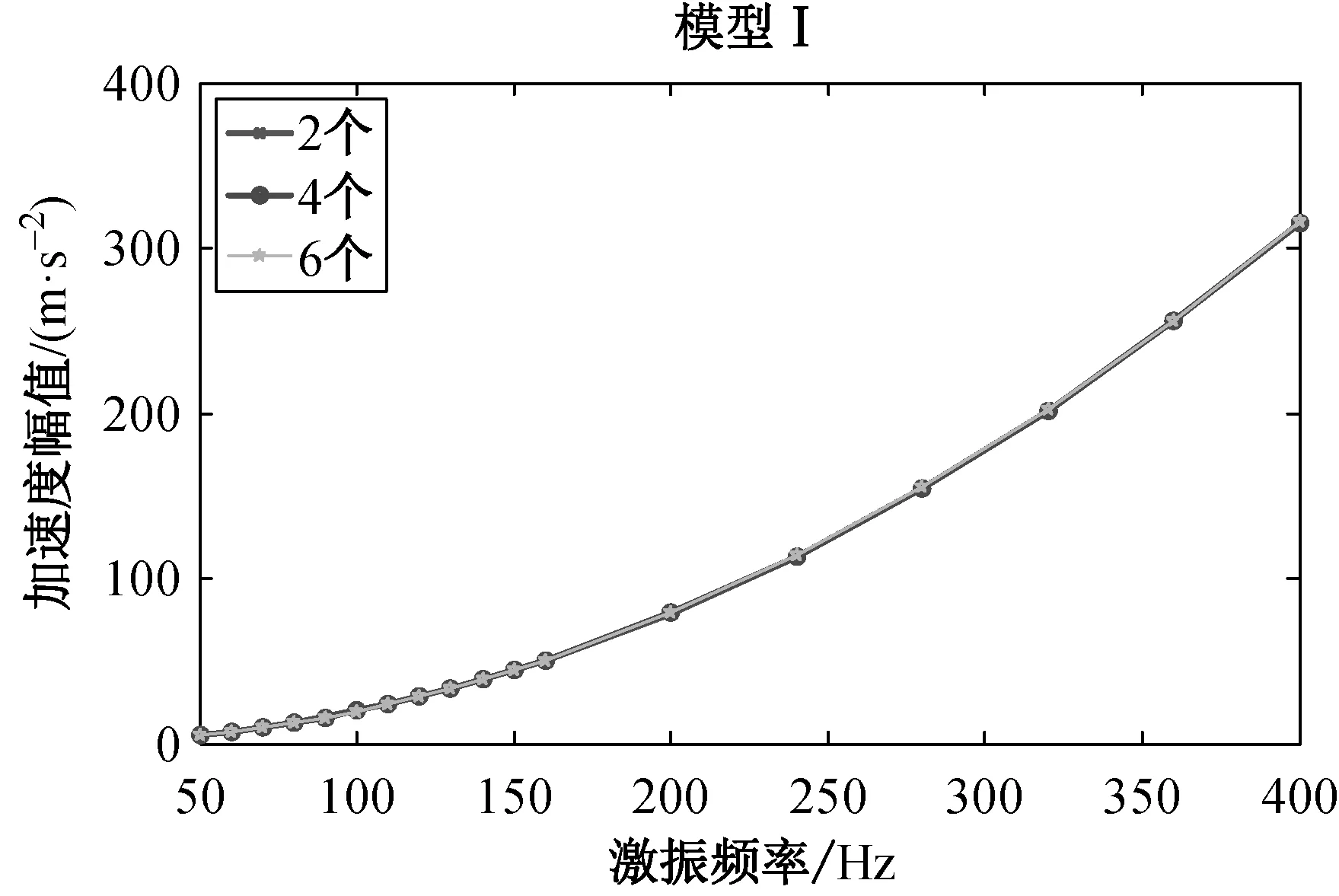
(a) 支承座加速度幅值

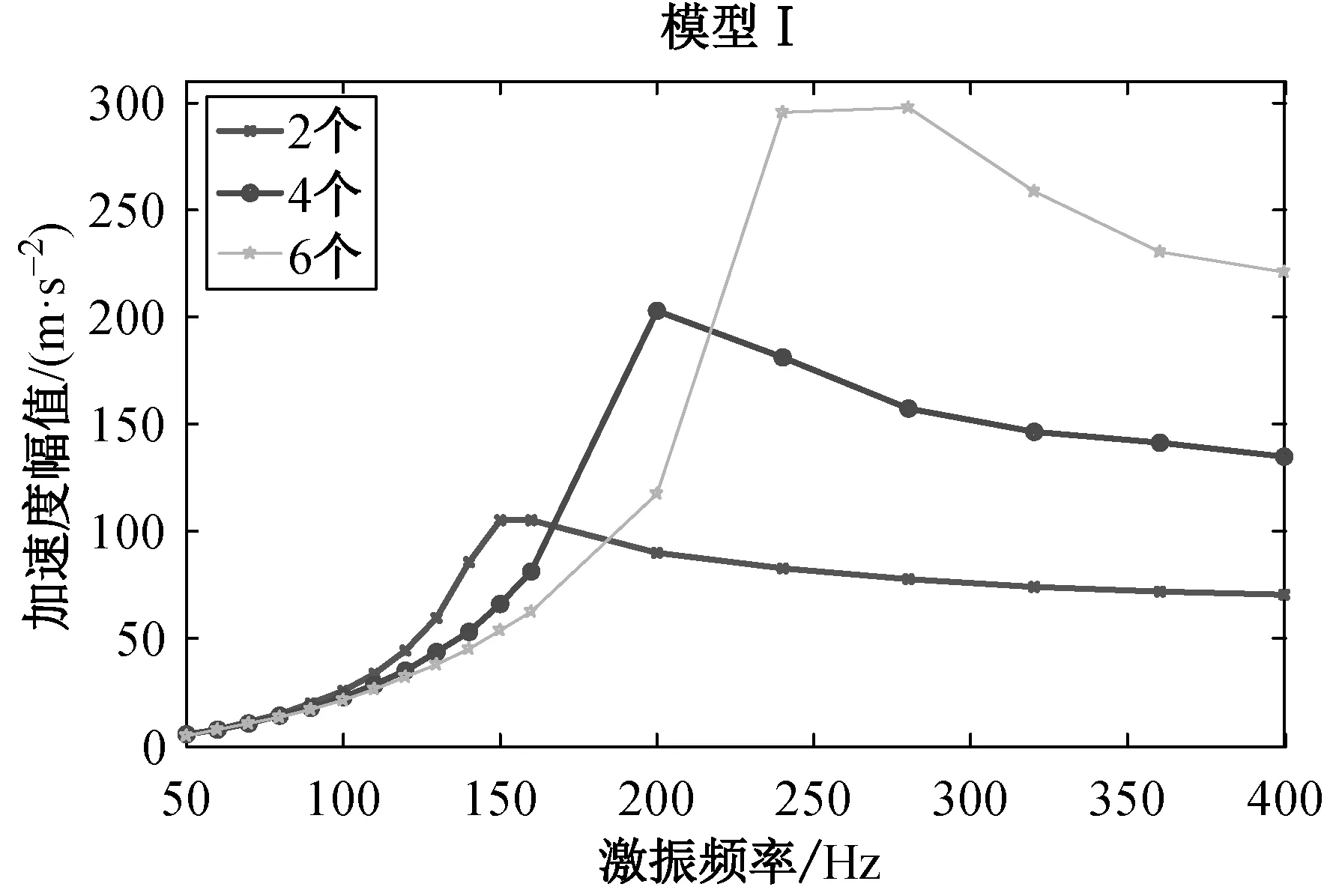
(b) 振动质量m加速度幅值 图7 模型Ⅰ加速度响应幅值频变图

Fig.7AccelerationresponseamplitudefrequencyvariationofmodelⅠ

由图7(a)可知，模型Ⅰ中O型橡胶圈数量分别为2、4 和6个时支承座的加速度响应幅值数据变化趋势基本一致。由图7(b)可知，在振动台激振频率为50～400 Hz下，模型Ⅰ中O型橡胶圈数量为2、4、6个时振动质量m的加速度响应幅值随频率的增加先增加而后减小，分别在激振频率f12=160 Hz、f13=200 Hz、f15=280 Hz时达到最大值，随后趋于稳定。

4.2 等效刚度与等效阻尼计算

根据模型Ⅰ中O型橡胶圈数量分别为2、4和6个时支承座和振动质量m的加速度响应幅值试验数据，由式(3)可计算出不同数量的橡胶圈所构成的柔性支承系统的刚度和阻尼系数，其频变曲线如图8所示。

(a) 刚度

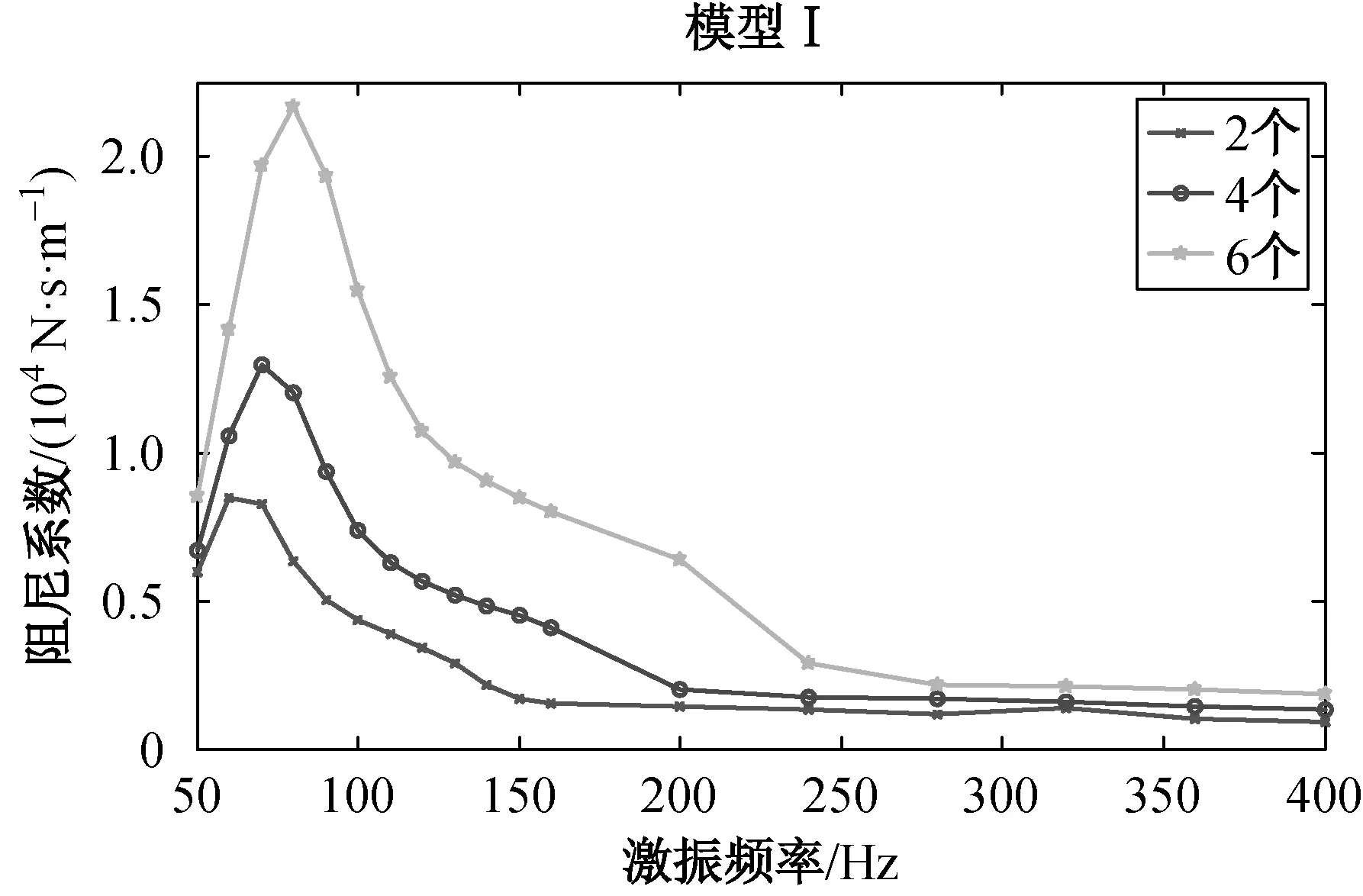
(b) 阻尼 图8 模型Ⅰ支承刚度和阻尼系数频变曲线

Fig.8FrequencycurveofsupportstiffnessanddampingcoefficientofmodelⅠ

由图8可以看出：在50～400 Hz的激振频率下，含O型橡胶圈的柔性支承系统支承刚度的变化趋势随频率的增加先升高而后降低，最后趋于缓慢增加；阻尼系数的变化趋势为随频率的增加先升高而后降低，最终趋于平缓；模型Ⅰ中O型橡胶圈数量为2、4和6个时激振频率分别在f12=160 Hz、f13=200 Hz、f15=280 Hz后，系统的支承刚度和阻尼系数与O型橡胶圈数量成正比关系。

采用相同测试方法，根据实际锭轴的橡胶圈配置数量(见表1)，在该工作频率范围内检测其他3类模型(含2个φ46、 6个φ47、 6个φ54)柔性支承系统的动力学参数，特别说明，ZWT 612-180型卷绕机锭轴上实际采用10个φ47的橡胶圈，为使试验测试装置平衡，仍安装6个橡胶圈(每端安装3个)来进行测试。根据测得的支承座和振动质量m的加速度响应幅值。由式(3)计算出相应柔性支承系统的刚度和阻尼系数，分别绘制频变曲线如图9所示。

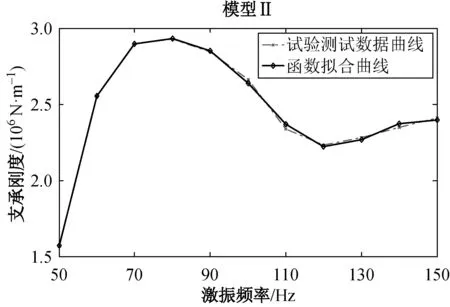
(a) 刚度

(b) 阻尼

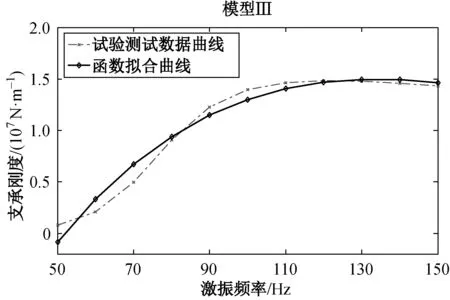
(c) 刚度

(e) 刚度

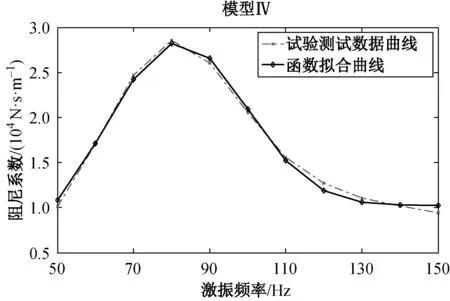
(f) 阻尼 图9 模型Ⅱ、Ⅲ与Ⅳ的支承刚度和阻尼系数频变曲线

Fig.9FrequencycurveofsupportstiffnessanddampingcoefficientofmodelⅡ，ⅢandⅣ

由图8和9可知，在ZWT 612-180型卷绕机主要工作频率50～150 Hz内，含O型橡胶圈的柔性支承系统动力学参数(刚度和阻尼系数)具有以下：

(1) 柔性支承系统动力学参数具有频变特性，其参数值随激振频率的变化而呈非线性变化特点；

(2) 采用相同数量的橡胶圈配置情况下，含O型橡胶圈的柔性支承系统的支承刚度和阻尼系数随配置橡胶圈截面尺寸的增大而增加，并表现出结构参数的非线性特点；

(3) 采用相同结构参数的橡胶圈，含O型橡胶圈的柔性支承系统的支承刚度和阻尼系数随橡胶圈配置数量的增加而增大，但不具有倍数关系，且刚度和阻尼系数与激振频率呈非线性关系。

4.3 支承刚度与阻尼系数频变曲线拟合

综合分析含有4种不同结构参数橡胶圈的柔性支承系统的动力学参数测试数据，分别考察刚度k(f)和阻尼系数c(f)随频率f的变化规律，4条支承刚度曲线、4条阻尼系数曲线分别具有相类似的特点和趋势，故将刚度k(f)和阻尼系数c(f)随频率f的变化规律拟合曲线方程用统一的方程式表达，运用Matlab计算平台，拟合曲线方程为

(4)

式中：j代表不同模型代号，j=1， 2， 3， 4(见表1)；f为柔性支承激振频率50～150 Hz；a1、a2、a3、a4为支承刚度k(f)拟合曲线方程待定系数，b1、b2、b3、b4为阻尼系数c(f)拟合曲线方程待定系数。

4种含不同参数和数量橡胶圈的柔性支承系统待定系数各不相同，运用Matlab拟合函数，采用最小二乘法原理，得到的柔性支承系统的支承刚度与阻尼系数拟合曲线方程的待定系数如表2和3所示。

表2 拟合曲线方程式(支承刚度)待定系数Coefficients in fitting curve equation of stiffness

表3 拟合曲线方程式(阻尼系数)待定系数Coefficients in fitting curve equation of clamping

根据支承刚度和阻尼系数拟合公式(4)与表2和3的系数，可绘制出相应柔性支承系统的刚度和阻尼系数频变拟合曲线。图12所示为工作范围内模型Ⅰ的动力学参数根据拟合公式绘制的拟合曲线，对比发现，其与测试数据吻合较好。

(a) 刚度

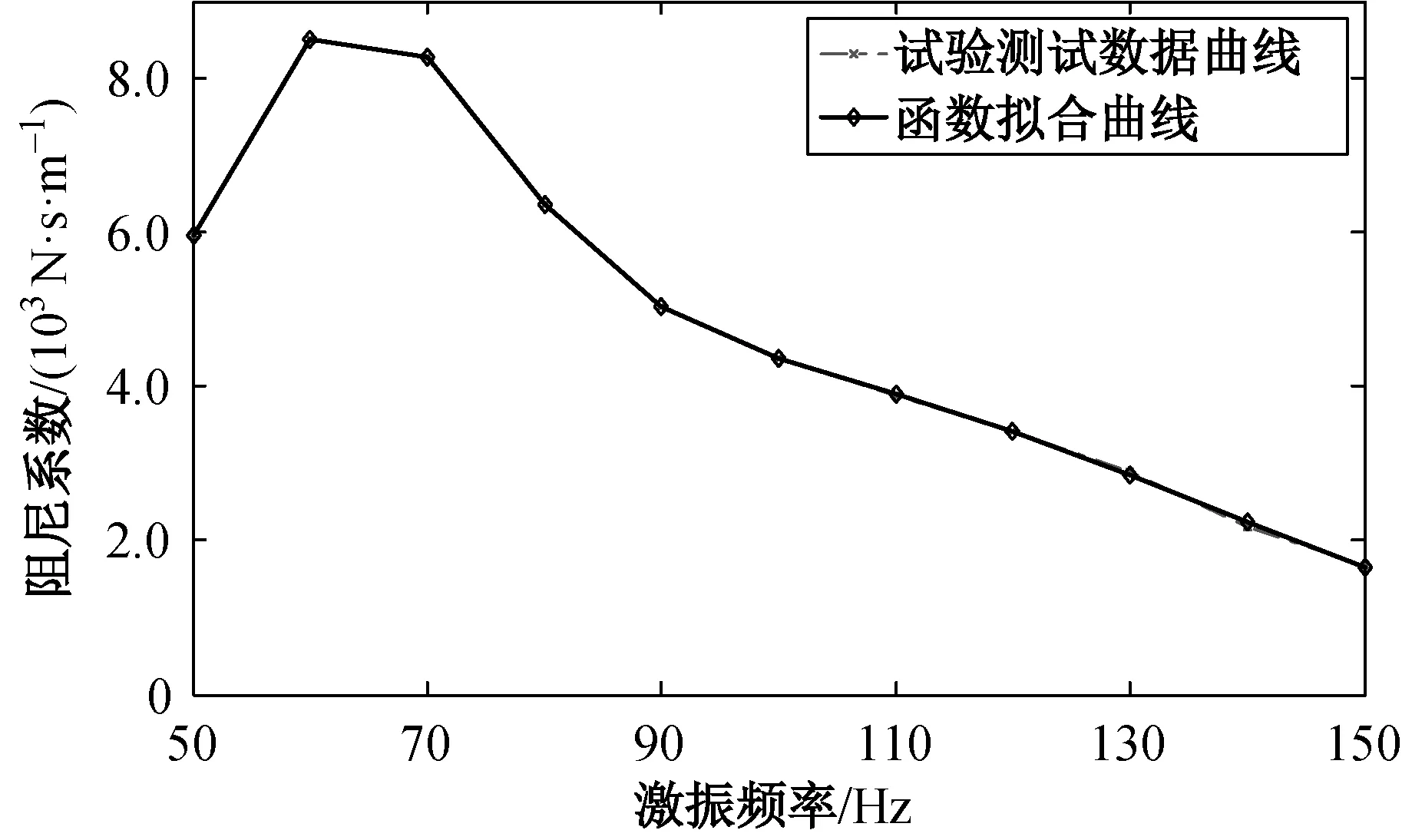
(b) 阻尼 图12 工作范围内模型Ⅰ刚度及阻尼系数拟合频变曲线

Fig.12FittingfrequencycurveofstiffnessanddampingcoefficientofmodelⅠinworkingrange

5 结 语

本文对ZWT 612-180型卷绕机锭轴上的O型橡胶圈柔性支承系统动力学参数的频变特性进行了测试与分析，测试模型结构尺寸完全依照卷绕机实际尺寸设计，经分析可知：

(1) 在主要工作频率50～150 Hz内，含O型橡胶圈的柔性支承系统动力学参数(刚度和阻尼系数)具有频变特性，并呈非线性变化。柔性支承系统的动力学参数值与橡胶圈配置数量不呈倍数关系，这为卷绕机锭轴结构设计带来一定难度。

(2) 根据测试采集到不同激振频率下的试验数据，由非线性回归方程作为参考，拟合出含O型橡胶圈支承系统的动力学参数频变曲线，并给出了相应计算公式，为进一步分析和优化设计含有橡胶圈的柔性支承锭轴卷绕转子打下基础。