基于改进KNN算法的城轨进站客流实时预测
郇 宁,谢 俏,叶红霞,姚恩建*
(1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044;2.广州地铁集团有限公司,广州510030)
0 引言
随着城市轨道交通网络化运营规模不断扩大,准确地掌握客流分布状况成为提高客运组织水平的重要前提.高精度、小粒度的实时进站量预测能够帮助管理者及时掌握网络客流演化态势,为客运组织提供重要的决策依据.
针对客流预测问题,国内外学者对短期和中长期的需求预测关注较多.蔡昌俊[1]通过构建乘积ARIMA模型,消除趋势性特征影响,推演客流长期变化规律.姚恩建等[2]考虑车站可达性指标,建立新线接入后既有站的进出站量预测模型.光志瑞[3]针对节假日客流中动态特征的非线性序列,分析了制约预测精度的关键因素.徐瑞华等[4]提出了站台—列车客流交互模型,为断面客流等精细化指标预测提供了理论基础.包磊[5]通过灰色模型和马尔科夫链预测线路客运量等宏观指标.此类研究普遍针对客流周期性变化,旨在为运力配置提供测算依据,而对实时运算逻辑和效率约束等因素关注较少,难以适应动态增量的数据环境.
近年来,非参数回归模型凭借其灵活性和强大的数据处理能力,在实时预测领域应用广泛.Davis G.A.[6]于1991年将非参数回归模型应用到交通流量预测中,并系统地梳理了相关基础理论.宫晓燕等[7]针对基于动态聚类和散列函数的数据组织方式,提出了基于密集度的变K搜索算法.张涛等[8]分析了K最近邻(K-nearest-neighbor,KNN)算法中状态向量等关键因素对精度的影响.谢俏等[9]将KNN算法应用于城轨车站的进出站量实时预测问题,考虑了客流的时间关联性,取得良好的预测效果.目前,同类研究所提出的模型普遍针对15 min或1 h粒度的客流数据,由于采样时间跨度较大,样本的数值型特征相对明显,因而对实时数据中噪声扰动等因素考虑不足,其预测机制也往往难以适用于现实环境.此外,在传统KNN算法的模式匹配过程中,普遍采用基于欧式距离的“点对点”度量方法,当序列中波峰、波谷在时间轴上产生偏移时,造成误差显著升高.本文以5 min粒度的实时进站量数据为研究对象,结合序列降维拟合技术和动态时间规整算法,改进传统KNN算法的模式匹配环节,在规避噪声扰动的同时,实现考虑序列形态的样本匹配;在回归预测阶段,引入距离权重和趋势系数以顺应客流的自然增长规律;最后,通过精度分析论证了方法的可行性与有效性.
1 城轨进站客流变化规律分析
深入分析客流变化规律是客流预测的重要前提.其一,进站客流规律受周边土地性质等环境因素影响明显,以广州地铁线网中区域跨度较大的3号线为例,随机选择某日的分时进站量进行横向对比,如图1所示.由图1可知,5 min粒度下的进站量波动较强,并且站点的客流规模与峰值分布存在差异.因此,考虑以车站为基本单元组建历史样本库.在数据条件不足的情况下,可结合聚类等手段,选择与本站客流规律相近的同类站点扩充样本.其二,客流规律受双休日、节假日安排等因素影响明显,以位于中心商务区的珠江新城站为例,对不同日期进行纵向对比,如图2所示.
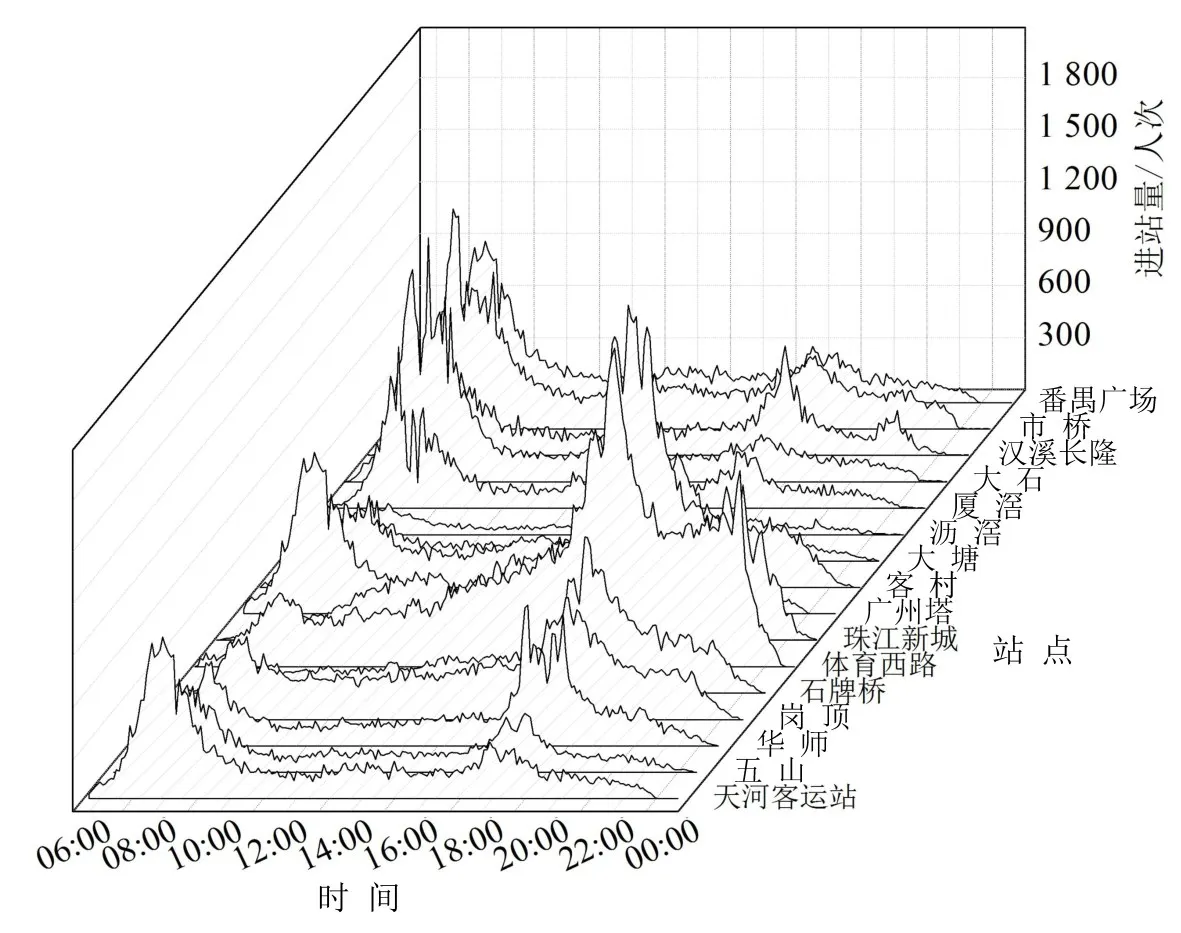
图1 广州地铁3号线站点分时进站量对比图Fig.1 Entrance passenger flow of stations in Guangzhou Metro Line 3
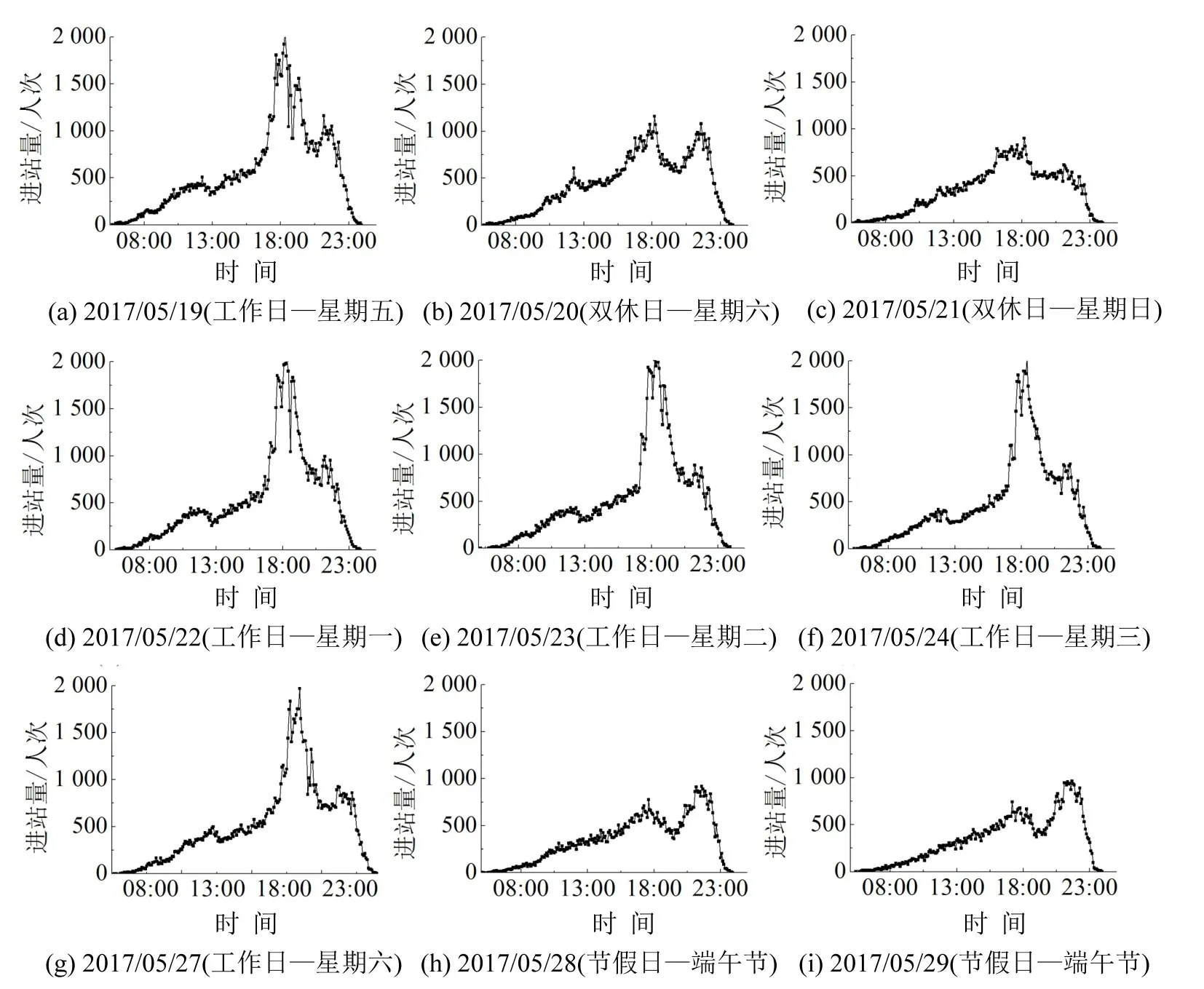
图2 珠江新城站分时进站量变化图Fig.2 Entrance passenger flow of Zhujiang New Town station among certain days
可见,珠江新城站基本不存在早高峰,但具有傍晚通勤和晚间出行带来的双高峰特征.图2中:(a)、(d)、(e)、(f)分别对应不同星期数的工作日,客流规律较为相近;(b)、(c)为双休日,傍晚通勤高峰明显弱于工作日;(g)虽为周六,但受端午节调休影响,规律与工作日一致;(h)、(i)为端午假期,晨间客流进一步衰减,存在晚间高峰强于傍晚高峰的特殊现象.基于此,将预测场景初步划分为工作日、双休日、节假日3类.
2 城轨进站客流实时预测模型
结合进站客流数据特性,构建基于改进KNN算法的实时预测模型.首先,确定状态向量选取规则以合理描述样本特征;其次,为解决“点对点”欧氏距离匹配适用性差的问题,提出改进的模式匹配方法,实现考虑序列形态的精准匹配;最后,根据近邻样本与预测目标的差异引入距离权重和趋势系数,给出一般化的预测算法.
2.1 状态向量选取
考虑到进站客流具有较强的时间关联性,故选择与当前邻近的m个时段的进站量构成状态向量,用于描述样本特征.通过计算历史分时进站量的自相关系数推算m值,公式为[9]
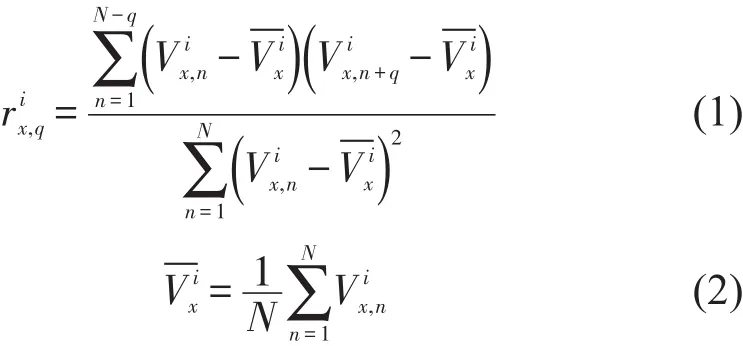
以2016—2017年全网的分时进站量数据为对象,将每日每站216条(6:00-24:00)分时进站量视为1个序列样本.根据式(1)和式(2)计算自相关系数.当≥0.5时,通常认为序列中相邻的q个时段相关性显著[9].统计符合该条件的样本比例,结果如表1所示.

表1 广州地铁分时进站客流自相关性统计表Table 1 Self correlation feature of entrance passenger flow in Guangzhou metro(%)
表1结果显示,5 min粒度下的进站客流时间关联性明显.综合考虑样本分布及实际预测的精度表现,确定若样本总量的85%以上满足≥0.5,则认为邻近的前q个时段具有较强相关性,进而确定工作日、双休日、节假日对应的m值为9、8、7,并以此作为状态向量选取依据.
2.2 基于关键点的序列表示方法
考虑到进站量序列中离群点较多且波动频繁,若直接进行处理不仅会降低实时运算效率,而且影响预测效果.所以,在模式匹配之前,采用关键点法(Key Point Segmentation,KPS)对序列进行降维拟合处理,寻找关键极值点(Key Extreme Point,KEP)和关键转折点(Key Turning Point,KTP)对序列进行抽象化表示.首先,设置极值保持时段阈值K0,筛选KEP以去除序列中的过多细节;其次,利用夹角法描述序列转折趋势,通过转折角度阈值θ0筛选KTP,如图3所示.
对于图3中的子序列(xi-1,xi,xi+1),通过计算转折角的余弦值量化转折程度,公式为[10]


图3 KTP选取指标计算示意图Fig.3 Illustration of parameter calculation for KTP selection
定义序列压缩比C和拟合优度R2评价降噪拟合算法的有效性.压缩比用于描述对序列的剪裁能力,低压缩比意味着低的计算成本,但过低亦会造成信息损失;拟合优度用于描述对序列的还原程度,值越接近1,表示拟合效果越好.公式为
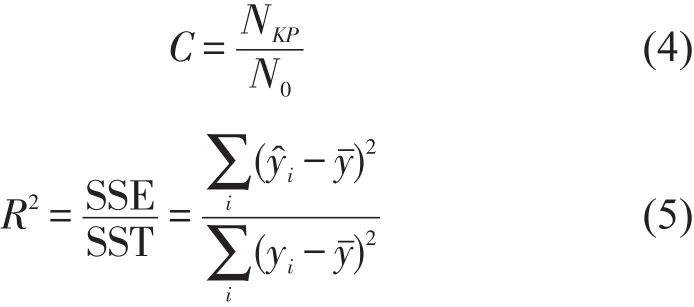
式中:N0为原始序列的维数;NKP为关键点集的元素数;yi和分别为序列点的原始值和拟合值;为原始序列的均值.
随机选取部分日期进行测试,指标如图4所示.确定参数K0取2,θ0取90°时,能够在获得较高拟合优度时,取得良好的压缩比.
2.3 基于动态时间规整的相似性度量方法
模式匹配是KNN算法的核心步骤,指寻找特征空间中K个最邻近样本的过程.对于时间序列这一研究对象,通常采用序列间相似性度量实现.针对序列样本在时间轴上的偏移、扭曲等现象,采用动态时间规整(Dynamic Time Warping,DTW)算法对非等长序列进行相似性度量,适当扩张或压缩局部特征,进而得到更好的形态度量效果,如图5所示.

图4 KPS序列表示方法指标统计图Fig.4 Evaluation index for KPS algorithm
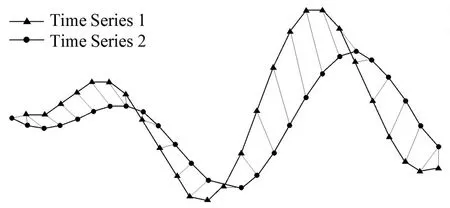
图5 DTW相似性度量示意图Fig.5 Diagram of similarity measurement with DTW algorithm
对于序列A=(a1,…,ai,…,am)和B=(b1,…,bj,…,bn),构建m×n的距离矩阵Dm×n,DTW的目的在于寻找一条通过若干格点的路径P=(p1,…,pk,…,pK),使得其全局代价最小,即令累积距离C满足条件
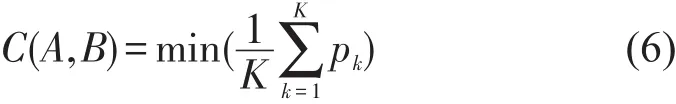
式中:pk为该路径元素在矩阵中的位置,即表示ai和bj间的匹配关系.
一般而言,序列间存在多条路径,但有效路径P应满足边界性、连续性和单调性约束[11].采用动态规划方法构造一个代价矩阵γm×n,即序列间DTW距离,公式为
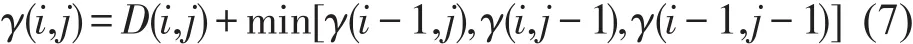
式中:D(i,j)为ai和bj间的距离,3种匹配方式如图6所示.

图6 子序列匹配方式示意图Fig.6 Illustration of matching patterns for subsequences
2.4 预测算法
以每个预测节点可获取的最新时段进站量为对象,通过调整K值对该时段进行迭代预测,取预测误差最小的K值作为应用值.同时,为顺应客流的自然增长规律,引入距离权重与趋势系数以修正预测结果.若匹配所得近邻日期为{z1,z2,…,zk},预测值的计算公式为


3 精度分析
依托广州地铁客流数据仓库对预测模型进行精度分析,以站点的全天分时平均绝对百分比误差ET和累积全天平均绝对百分比误差ED为评价指标,公式为
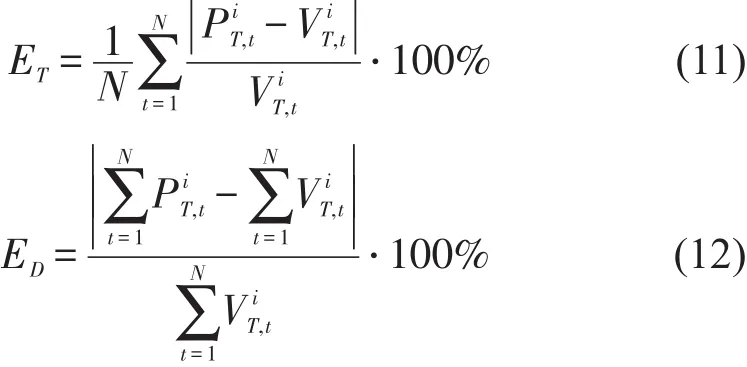
首先,测试模型于不同时间粒度下的预测效果,结果如表2所示.
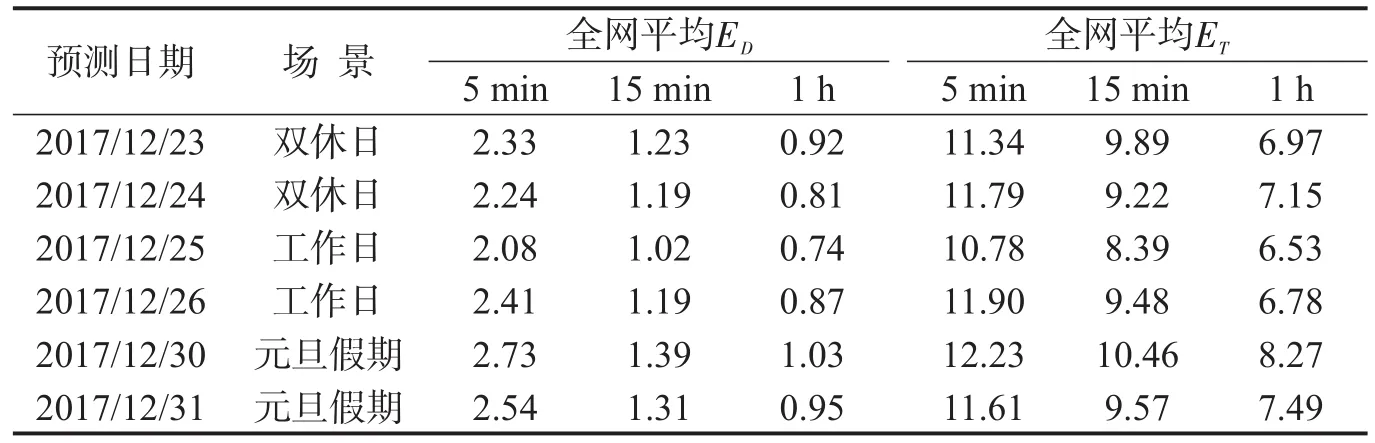
表2 不同时间粒度下的预测误差Table 2 Forecast error under different granularities(%)
与本文预测模式较为相近的文献[9]中,15 min粒度下全网平均ET为12.4%,证明本文提出的方法具有更强的时效性与准确性.在后续分析中,默认采用5 min时间粒度.
其次,对比KNN算法改进前后预测效果.具体分为以下4类:方法(i)为“逐点欧式距离匹配+近邻距离加权”的传统模式,方法(ii)为“KPS-DTW+近邻距离加权”的模式,方法(iii)为“逐点欧式距离匹配+近邻距离加权-趋势系数”的模式,方法(iv)为“KPS-DTW+近邻距离加权-趋势系数”的改进模式.结果如表3所示.

表3 不同方法下的预测误差Table 3 Forecast error with different algorithms(%)
由表3可知,匹配模式的改进对预测精度有较大提升,趋势系数的引入也具有良好的效果.然后,从线路层面进行分析,结果如表4所示.

表4 不同线路的预测误差Table 4 Forecast error of each line
由表4可知,客流量较大的站点往往预测精度更优.以7号线的谢村站为例,每日约90个时段的进站量小于5人次,致使该站误差较高,但在应用中可忽略此类影响.
此外,以客流规律不同的4个典型车站为例,随机选择某日的完整预测结果进行展示,如图7~图10所示.

图7 珠江新城站预测样本图Fig.7 Forecasting sample of Zhujiang New Town station
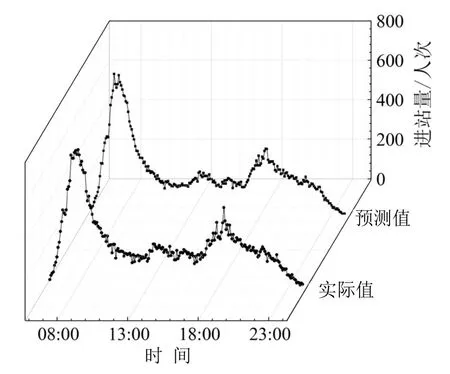
图8 东晓南站预测样本图Fig.8 Forecasting sample of Dongxiaonan station
可以看出,该方法在不同类型车站的预测中均表现出良好的效果,基本不存在局部偏离现象.
最后,探究模型在不同数据条件下的适用性问题.依据2017年长期的实时预测记录,对不同时期历史数据在预测中发挥的实际效用进行分析,统计其被成功匹配为近邻的频率,结果如图11所示.

图9 杨箕站预测样本图Fig.9 Forecasting sample of Yangji station
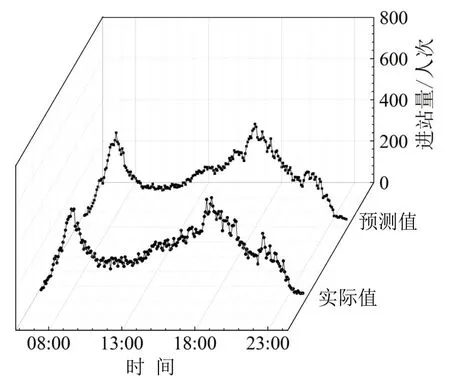
图10 长寿路站预测样本图Fig.10 Forecasting sample of Changshou Road station
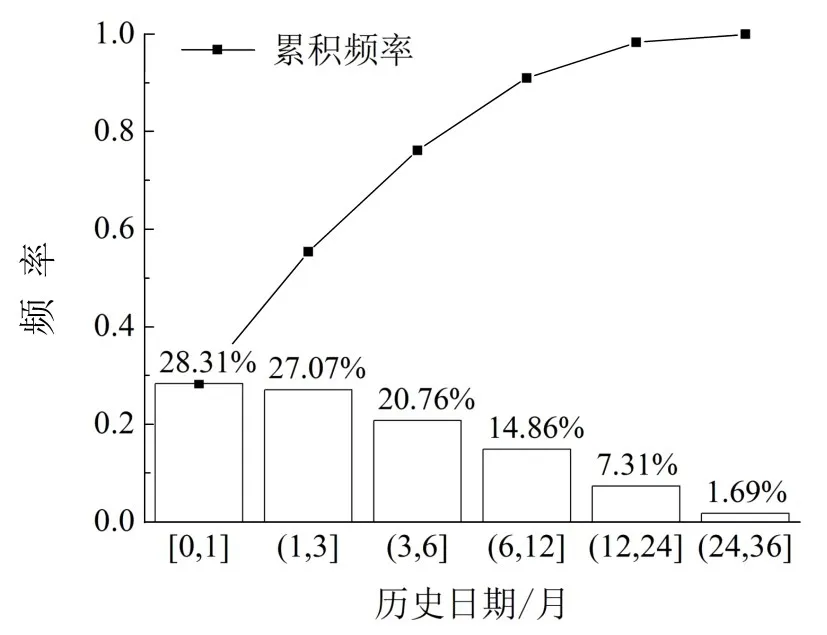
图11 历史样本选取频率分布直方图Fig.11 Frequency distribution histogram of sample selection
从图11可知,实际被匹配的样本中,九成以上处于预测日期前一年内.因此,为保证预测准确性,历史数据库应尽量覆盖近一年的客流数据.对于节假日等特殊场景,则需结合实际情况提供更长时限的同类场景历史样本.
4 结 论
针对小粒度客流数据的高维数、多噪声等特征,本文提出一种基于改进KNN算法的实时进站客流预测方法.其一,通过KPS序列表示法实现序列的降维表示,当拟合优度达0.8时,平均压缩比为62.4%,可在充分保留特征的同时规避细节扰动;其二,采用DTW算法解决不同维数序列间的相似性度量问题,可容忍小粒度客流数据中的偏移、拉伸现象,优化匹配逻辑;其三,在真实的动态数据环境中开展精度检测,5 min粒度下全网站点全天分时进站量预测的平均绝对百分比误差的均值为11.6%,并给出了历史样本库构建的参考规则.综上,该模型具有较好的可行性与有效性,能够为路网状态监控提供可靠的数据支撑.

