城市轨道交通运输网络级联失效抗毁性研究
刘朝阳,吕永波*,刘步实,李 倩,吕万钧
(1.北京交通大学交通运输学院,北京100044;2.北京城建设计发展集团股份有限公司,重庆401147)
0 引 言
城市轨道交通具有快速、大运量和污染小等优势,能有效缓解城市交通拥堵问题,部分城市的轨道交通网络化正逐步形成并向网络化运营阶段迈进[1].作为客流量特别密集的运输载体,轨道交通网络化的布局形式使得节点之间具有紧密的联系.而轨道交通的客流量较大,这就要求相关的安全保障机制非常严苛,大力提升安全防护措施的有效性.一旦遭受到外界恶意破坏,或者是在城市轨道交通运营过程中系统设备故障,抑或是突发性的客流剧增,任何节点的故障都可能在网络中迅速传播与扩散,最终导致非常严重的后果[2].在网络中,一个或少数节点或连线的失效会通过节点之间的耦合关系引发其他节点也发生失效,进而产生级联效应,最终导致一部分节点甚至整个网络的崩溃,这种现象就称为级联失效,有时也形象称之为“雪崩”[3].对级联失效的研究早期可追溯至电力、信息网络等复杂网络级联效应的研究[4-5].同样,城市轨道交通网络也存在类似的现象,网络中节点或者区间中断运营会引发其他节点不堪流量压力而产生级联拥堵[6].
因此,为了保证城市轨道交通的安全运营,本文综合考虑了轨道交通的基本性质及动力学行为,而非仅仅停留在静态研究上,从而减少整个交通网络的损失.同时,本文的研究还为轨道交通的应急预案设计、网络规划和合理改扩建提供了良好的参考依据.
1 城市轨道交通网络级联失效模型
本节将结合城市轨道交通特性,构建城市轨道交通网络级联失效模型.由于节点的失效会更快速更严重的引发级联失效,因此本文分析节点失效下的级联失效过程,并假设网络中任何节点失效,在本文的研究期内都不具有恢复能力.
1.1 交通流分配
轨道交通网络节点少,网络中边的数量不多,在某一节点失效时,OD之间可替代的其他路径有限,又由于边权主要考虑时间因素,其他可替代路线的通行时间一般远远大于最短路的通行时间,这种情况下乘客会优先考虑最短路径.全有全无配流方法算法简单且适用网络结构简单、规模不大的轨道交通网络,因此本文选择全有全无的客流分配方式[7],分配交通量的步骤如下:
Step1 初始化网络,确定网络中各条边的时间阻抗.
Step2 运用Floyd算法计算网络中每个出发地O到每个目的地D之间的最短路径.
Step3 将O、D之间的OD交通量全部分配到相应的最短路径上.
在对流量进行分配时,城市轨道交通网络中的换乘站需要区别于普通车站.由于换乘站的换乘次数和换乘时间对出行路径的选择有很大的影响,因此对换乘节点需要进行加权.为了恰当地处理换乘站在网络模型中的权重问题,本文引入换乘边的概念,如图1所示,将换乘站拆分为若干个虚拟的站点,分别位于换乘站所处的不同线路上,彼此之间用换乘边连接,每条换乘边两端的两个站点名称相同,但是在对网络中站点进行编号时,站点的编号不同.

图1 换乘站在网络模型中的处理Fig.1 The processing of the transfer station in the network model
1.2 相关变量定义
1.2.1 城市轨道交通网络节点流量
在实际的城市轨道交通网络中,城市轨道交通网络的负荷为各节点及各区间的客流量.因此本文假设乘客总是选择出行起点至出行终点的最短路径来完成出行,定义节点vi的初始流量Li(0)为所有OD对按照出行路径最短分配后,经过节点vi的交通量.

式中:Li(0)为节点的初始流量;lkj为节点vk与节点vj路径上的流量;如果节点vi在节点vk与节点vj路径上,则=1,否则=0.
1.2.2 城市轨道交通节点容量
车站客流集散能力是指车站在整体设备都正常的情况下车站所能通过的最大客流量[8],本文假设城市轨道交通网络中各节点都存在一定客流承载能力,能力的大小受成本限制,设计者在前期规划设计轨道交通车站时,根据预测的客流量及一定的预留空间确定车站的规模,城市轨道交通网络中节点的容量是“按需定容”,节点的容量与节点的预测客流量及备用能力系数有关,在确定节点的容量时,假设节点的容量与初始流量的关系为

式中:Ci为节点vi的容量;α为备用能力系数,α>0.轨道交通网络中节点具有基本固定的承载能力,即节点的容量确定后是不变的.
1.3 流量重分配方法
在城市轨道交通网络中,对于原本需要经过失效节点的乘客,不得不在拓扑结构发生改变后的网络中重新选择1条最短路径,因此会增加其他路径上节点的交通压力,当经过某节点的流量达到其容量时,则会导致该节点拥堵“失效”.轨道交通网络的节点流量过大只会导致乘客经过该节点的拥挤成本增加,乘客经过该节点的综合阻抗变大,不会导致该节点完全丧失运输功能.节点的综合阻抗变大通过与该节点相连接的边的权值变大体现,因此本文对此做出改进,通过式(3)来表示节点状态变化及相连的边权的变化.
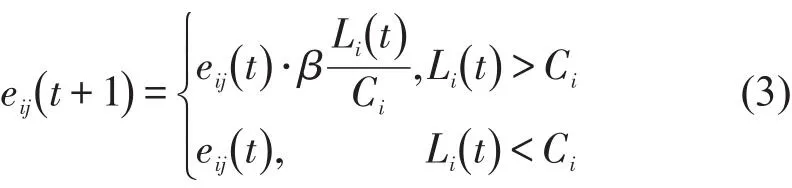
式中:eij(t+1)表示与节点vi相邻的边在t+1时刻的边权;eij(t)为网络中相应边的t时刻的边权;β为罚系数,当Li(t)/Ci值小于使网络最短路发生变化的临界值时,β充分大,边权明显增大,否则,β=1.
节点阻抗的变化与该节点的拥挤度相关,节点越拥挤,该节点的综合阻抗也越大.当节点的失效导致其他节点拥堵“失效”时,与拥堵失效节点的相连的边权值变大,导致网络中的最短路径发生变化,产生新一轮的重新分配,直到没有新的失效节点产生,这个过程才结束.节点的“失效”状态,分为两种情况:
(1)由于外界的蓄意破坏或者自身设备故障导致节点失效,将该节点及其相邻的边从网络中删除.
(2)因节点失效导致其他节点流量超过容量而拥堵“失效”,不将其从网络中删除,而是增大该节点的阻抗.
网络中节点的状态如图2所示.

图2 节点状态示意图Fig.2 Node state schematic diagram
1.4 级联失效算法及仿真流程
根据本文建立的城市轨道交通网络级联失效模型,确定级联失效模型算法如下:
Step1 给定城市轨道交通网络,确定网络中各边的边权大小,形成无向加权网络.
Step2 应用Floyd算法找到网络中任意两节点之间的最短路径,按照全有全无分配方法将交通需求分配到网络中,得到网络各节点的初始流量和容量.
Step3 令网络中某节点失效,从网络中删除该节点及其相邻的边,形成新的网络.
Step4 重新计算网络的最短路径集,将交通量分配到网络中,得到各节点的流量,统计当前时刻流量大于容量的节点.
Step5 判断节点的状态,对于流量大于容量的节点,根据式(3)更新网络中相应边的权值大小,确保产生新的“失效”点,形成新的网络.对于经过该“失效”点的OD最短路,重复Step4直到没有新的失效节点产生,否则失效过程结束.仿真流程如图3所示.
1.5 级联失效抗毁性评估指标
本文综合考虑了评价指标的合理性及计算复杂程度,选择从网络失效规模和破坏程度两个方面来评估级联失效对网络的影响.
(1)有效节点比.
有效节点比是指节点失效后级联失效过程中网络的正常状态的节点数与初始网络中节点数的比值,该指标是从网络失效规模方面来评估级联失效对网络的影响.

式中:Ni为节点vi失效后级联失效过程中网络的正常状态节点的数;N为初始网络的节点数;Z1∈[0,1],有效节点比越高,表明网络级联失效抗毁性越强.

图3 级联失效仿真流程Fig.3 Schematic diagram of cascaded failure simulation process
(2)网络效率比.
网络效率是衡量城市轨道交通网络级联失效后破坏程度的一个有效指标,网络中节点vi和节点vj之间最短距离的倒数为两点之间的效率,在本节中节点vi和节点vj之间最短距离为最小阻抗.对于整个城市轨道交通网络而言,所有节点对之间的效率平均值为网络效率,用E表示,计算公式为
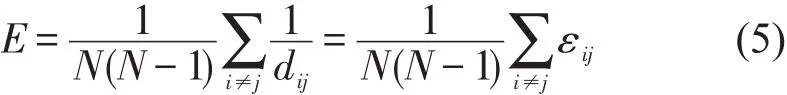
网络效率比为级联失效过程中的网络效率与初始网络效率的比值,其计算公式为

式中:Ei为节点vi失效后级联失效过程中的网络效率;Z2∈[0,1],该指标值越大,表明网络的级联失效抗毁性越强.
2 实证研究
北京地铁是我国最早的城市轨道交通系统,截止到2017年12月,已开通21条运营线路,共设置316个车站(换乘站不重复计算).为模拟北京市城市轨道交通网络节点的级联失效过程,构建北京市城市轨道交通网络模型如图4所示.

图4 北京市轨道交通网络模型Fig.4 Urban rail transit network model of Beijing
假设初始时网络中边的时间阻抗为3 min,换乘边的时间阻抗为5 min,每个OD对之间产生1个单位的交通量.按照网络中任意两点之间的最短路径将交通流量分配网络中,得到各节点的初始流量.再通过Matlab编程模拟选择性失效和随机性失效两种失效方式下的级联失效过程,得到级联失效抗毁性评估指标.
选择性失效为移除网络中重要度最高且流量最大的西直门节点,随机性失效是随机移除网络中某节点.本文随机性失效下的网络级联失效抗毁性评价结果为10次随机结果的平均值,随机移除的节点分别为永安里、郭公庄、魏公村、万源街、莲花桥、成寿寺、东湖渠、来广营、海淀五路居和次渠,涵盖了起始站、普通站和换乘站.两种失效方式下的有效节点比和网络效率比如图5和图6所示,其中每次迭代为1次流量重分配.
从图5和图6可以看出,当备用能力系数相同时(以0.2为例),选择性失效情况下,初始时网络的有效节点比与网络效率比下降较快,并随着迭代次数的增加逐渐趋于稳定.这说明了在节点失效的初期,由于失效节点的流量较大,这部分流量的重分配导致较多的节点发生了拥堵,使网络效率快速下降.在迭代次数5和6之间,有效节点比下降,然而网络效率趋于稳定,表明随着拥堵的传播,当网络中发生大范围的拥堵之后,拥堵节点的增加对网络效率不再有明显的影响,直到级联失效过程结束.在这个过程中,重要度高的节点失效比随机选择节点失效更容易引发级联失效且对网络的影响范围更广,对网络的整体破坏程度更严重,网络在选择性失效下的级联失效抗毁性较弱.

图5 不同失效方式下有效节点比Fig.5 The effective node ratio under different failure modes

图6 不同失效方式下网络效率比Fig.6 The network efficiency ratio under different failure modes
相比于选择性失效,随机性失效对网络的影响程度较小,某些节点的失效甚至不会引发级联效应,原因是北京市轨道交通网络中的大部分节点重要度较低具有较小的流量,随机性失效大多发生在这类节点上,这部分节点的失效对网络其他节点造成的流量压力较小,因此不会引发大规模的拥堵,网络在随机性失效下的级联失效抗毁性较强.
图7和图8显示了选择性失效情况下,不同的备用能力系数对网络级联失效抗毁性的影响,从图中可以看出,随着迭代次数的增加,网络的有效节点比和网络效率比随之降低,且备用能力系数越小曲线下降越快,表明对网络的影响范围越广及破坏程度越严重,原因是节点容量较小时,需要更多的节点的富余容量分担失效节点的流量,随着容量的增大,剩余节点的分担能力也随之增大,节点失效对网络的影响范围也就越小.

图7 不同备用能力系数下的有效节点比Fig.7 The effective node ratio under different reserve capacity coefficients

图8 不同备用能力系数下的网络效率比Fig.8 The network efficiency ratio under different reserve capacity coefficients
从图7和图8可以看出,当备用能力系数α为0.5时,网络的有效节点与网络效率比在级联失效传播初期明显高于其他备用能力系数下的有效节点比与网络效率比.因此在对轨道交通改扩建时,可适当增加网络中关键节点及关键节点失效后容易引发拥堵的节点的容量,在级联失效初期有效减少拥堵节点,以减小级联失效影响范围.此外,在级联失效传播后期,不同备用能力系数下的网络效率比逐渐趋于稳定,且当备用能力增大时,网络效率比没有明显提高,这表明当节点失效时,越早采取应急措施对减小级联失效的影响程度效果越显著,当拥堵增大一定范围时,网络容量的增加不能明显提高网络效率.图中更加直观、具体量化了选择性失效情况中有效节点比和效率比的各个趋势,有助于为实际运营过程中轨道交通网络的合理规划,以及应急方案的制定提供更详细、更客观、更有效的参考意义.因此在轨道交通网络实际运营过程中,应及时响应应急方案并准确定位拥堵节点,降低网络受影响程度,提高网络的级联失效抗毁性.
3 结论
本文结合轨道交通特性,建立了城市轨道交通网络级联失效模型,确定了交通流分配方法,对模型中的变量做出了定义,确立了节点失效下的流量重分配方法,并对北京市城市轨道交通网络不同失效方式下的级联失效过程进行了仿真.结果表明,当北京轨道交通网络某些重要度高的节点失效时,网络的有效节点比及网络效率比在级联失效过程中下降较快,网络的抗毁性较弱,对于节点随机性失效,网络的抗毁性较强.同时通过比较分析发现,在级联失效传播初期,网络容量的增大能较为明显的减小级联失效影响范围,当拥堵增大一定范围时,网络容量的增加不能明显提高网络效率.
—— “T”级联

