基于在线地图交通态势分析的路网拥堵状态识别

张建旭，郭力玮

(重庆交通大学运输学院，重庆400074)

0 引 言

路网拥堵状态识别是瓶颈点交通管理的重要前提，早期的状态识别主要依托于人工调查、感应线圈[1-2]等方式获取交通参数，运用传统的数理统计方法来实现，大大降低了路网交通拥堵状态识别的效率和范围.随着交通大数据的快速发展，浮动车数据、手持终端数据、非结构化视频数据、多源互联网数据等均成为交通状态识别研究的数据来源[3]，但是大多研究仅以历史交通大数据[4-5]的统计分析为基础对区域交通运行状态进行总结性评价，并未将其应用于实时的交通拥堵状态识别.此外，现有研究忽略了交通拥堵的形成规律，仅依据交通状态评价指标[6]或交通流参数[7]来量化拥堵状态.

目前部分城市建立交通信息中心以实时计算并发布城市的交通拥堵指数，如北京市的TOCC[8]等.但是这种方式耗费较多资金，对于多数中小城市无法通过此方法实时发布城市路网交通状态.在线地图数据当前只停留在为个体用户提供实时路况信息或为管理者提供较长周期性的交通评价报告等，对于其在实时路网拥堵状态识别的研究中还未被运用.

本文以在线地图交通势态中的道路实时运行速度作为数据基础，计算其对应的道路实时延时指数，然后结合路网系统拥堵形成的规律，提出了路网系统拥堵程度的量化方法，并将其用于实时路网拥堵状态的判别.

1 在线地图交通态势量化指标分析

在线地图交通运行状态通常是由道路延时指数进行表达，其具体数学模型为

式中：DIa为道路a的延时指数；Ta为道路a中交通的实际运行时间；为道路a中交通的自由流运行时间；va为道路a中交通的实际运行速度；为道路a中交通的自由流运行速度.

目前地图公司或交通管理者通常利用道路延时指数对不同城市之间交通拥堵状态进行横向对比，然而由于不同城市的路网特征和交通管理措施等存在差异，该指标不能真实呈现城市交通运行状态的差异.本研究借助Python软件爬取高德地图API接口提供的道路实时运行速度数据，通过式(1)将其转换为道路延时指数，并利用该指数对路网不同时刻的运行状态进行纵向分析，能有效体现路网拥堵发生、发展和消散过程.

根据作者对系列高德交通报告的分析，当DI≥2.0，其道路交通状况开始用红色显示，因此在后续研究中，以2.0作为道路交通开始呈现拥堵状态的临界值.

2 路网系统拥堵的特征分析

路网系统拥堵通常是指路网中出现多条道路或者多个交叉口的大面积常发性拥堵现象，本文将在此基础上对路网系统拥堵的形成原理进行探索，将其划分成传播性系统拥堵和非传播性系统拥堵.

2.1 传播性系统拥堵特征分析

不相邻的多条路段发生交通拥堵后，在后续时刻拥堵传播至各自上游路段，这种传播使得拥堵路段彼此连接，最终导致大面积路网拥堵，本文将其定义为传播性系统拥堵.该类拥堵主要形成原因是相邻节点间间距较短，道路不具备储存较多排队车辆的条件，从而导致拥堵传播蔓延.图1对路网传播性系统拥堵进行了示意，其中加粗路段为拥堵路段.

图1 拥堵传播示意图Fig.1 Congestion propagation diagram

下面分别对传播性系统拥堵中相邻路段发生有效拥堵状态的时间顺序、持续时间阈值和流量的流入流出关系界定了下述3个条件，且需要同时满足.

(1)条件1.

其中u∈Ua且Ua≠∅

式中：Ua为路段a的上游路段集合；为时刻t路段a的延时指数；和分别为时刻t和t+1路段a的上游路段u的延时指数.

(2)条件2.

式中：ΔT为相邻传播性路段拥堵持续的最大时刻数；Δt为传播性拥堵持续时长的阈值；为t时刻路段a的平均运行速度；为时刻t路段a的上游路段u的平均运行速度；Δvt为时刻t路段a与其上游路段u的平均运行速度差值；Lu,a为路段a的上游路段u的道路长度.

该条件表示：拥堵传播过程中，下游路段运行速度需要小于上游路段运行速度，形成反向交通波，取该反向波传播至上游路段12长度所用时长为传播性拥堵持续时长的阈值.

(3)条件3.

式中：qu,a为从上游路段u进入其下游路段a的实际流量；Pu,a为从上游路段u进入其下游路段a的实际流量比例；p为上游路段进入其下游路段的流量比例阈值.其中阈值p可采用高峰时间段内，所有交叉口转向流量比的15%位累计值.

2.2 非传播性系统拥堵特征分析

非传播性系统拥堵是指不具有传播特性的单路段的局部拥堵，通常发生在长度较长且有充分存车空间的道路，拥堵在蔓延至上游道路之前就得到缓解.该拥堵的特征通常表现为长时性和频发性，将满足下面2个条件的局部拥堵称之为非传播性系统拥堵.

(1)条件1.

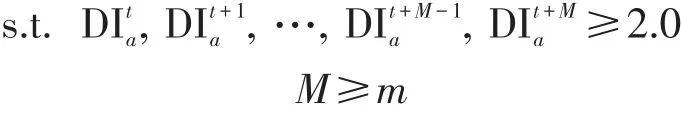
式中：M为路段a拥堵持续的最大时刻数；m为非传播性拥堵持续时刻数阈值.

(2)条件2.

式中：T为获取数据的时刻集合；Fa为路段a发生拥堵的频率；f为路段发生拥堵的频率阈值；为开关变量，其中t时刻路段a拥堵时变量值为1，否则变量值为0.

上述2个条件的阈值m和f可基于实际研究区域内单条路段拥堵发生现象的统计值确定.

3 路网系统拥堵的量化方法

3.1 路网系统拥堵路段集合定义

将数据获取时间段内所有时刻中满足上述路网系统拥堵特征的路段集合定义为N，将其中满足传播性特征的路段集合定义为S，将满足非传播性特征的路段定义为S~，则N=S⋃S~.该集合中储存了该区域的所有系统拥堵路段，且不同路段发生拥堵和拥堵消散的过程并不完全同步.

由于相同区域部分路段早、晚高峰可能存在潮汐现象，且各天早高峰(或晚高峰)的系统拥堵路段集合N可能有所差异，因此需将多天内早高峰(或晚高峰)的系统拥堵路段集合N进行比较，考虑由于突发事件引起路网偶发拥堵的情况，将拥堵路段数量异常过大所对应的集合或当天存在突发事件情况对应的集合进行剔除，在剩下的集合中选取元素数量最大的集合用Nmax表示，将其定义为系统拥堵极限状态对应的路段集合，对应的传播性路段集合和非传播性路段集合表示为Smax和

3.2 路网系统拥堵程度量化

以路段集合Nmax包括的所有路段为对象，通过构建模型可以量化研究区域内任意时刻发生系统拥堵的程度.由于路网系统拥堵集合Nmax包括传播性系统拥堵集合Smax和非传播性系统拥堵集合S~max两部分，将分别从两方面进行量化建模.

(1)传播性系统拥堵量化模型.

针对某一时刻传播性系统拥堵程度的量化，由于相邻道路具有传播特性，直接用两条相邻路段延时指数的算术平均值代表一对相邻传播路段的交通运行状态.据此提出传播性系统拥堵的量化模型为

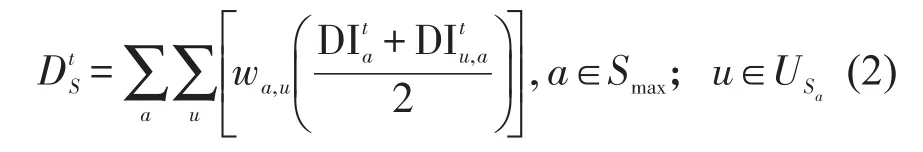
式中：USa为路段a的上游拥堵传播路段集合；wa,u为路段a与其上游路段u的延时指数均值所占权重；为t时刻传播性系统拥堵程度.

在权重wa,u的确定方法中，相邻路段的传播关联程度越大，其拥堵程度所占权重应该越大，因此，传播关联程度的量化可用皮尔逊相关系数实现.则权重wa,u的计算模型可表示为

其中∀a∈Smax,∀u∈USa

式中：tS为路段a与其上游路段u发生拥堵传播的开始时刻；ra,u为[tS,tS+ΔT]内路段a与其上游路段u的延时指数相关系数；为内路段a的平均延时指数；为内路段a的上游路段u的平均延时指数.

在数据获取的整个时刻中，由于相邻路段发生拥堵传播的时间段可能存在多个，计算的ra,u也存在多个，因此需要从中选取较为恰当的ra,u用于的计算.考虑到ra,u需要更能体现时刻t相邻路段的拥堵传播关联程度，其选取方法按如下定义：被选取的ra,u所对应的时间段应满足距离时刻t最近的特征，具体如图2所示.

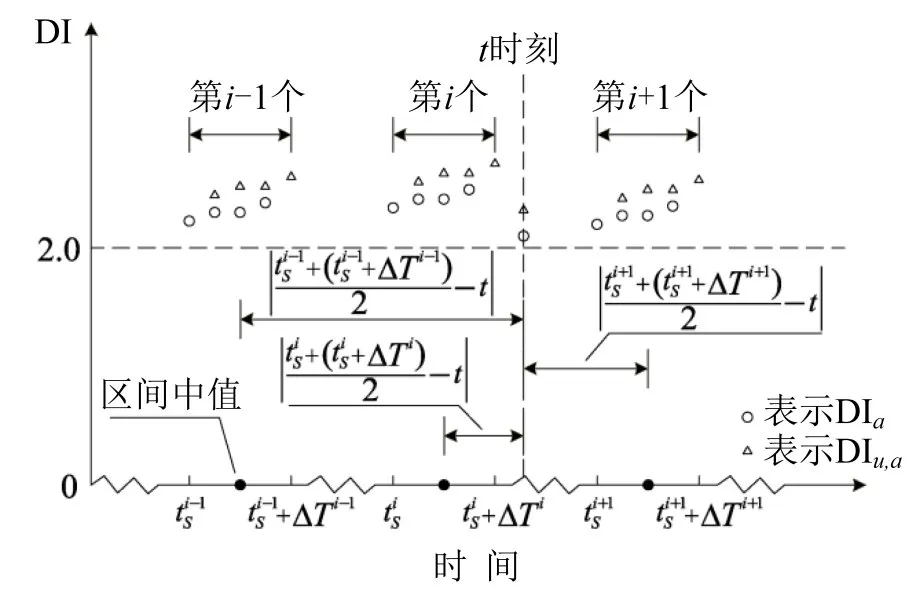
图2 t时刻ra,u的时间区间选取Fig.2 The time interval selection ofra,ufor timet

图2中路段a与其路段u在t时刻附近发生拥堵传播的时间段有3个，即和，其中3个时间段的中间时刻与t时刻的时间间隔满足

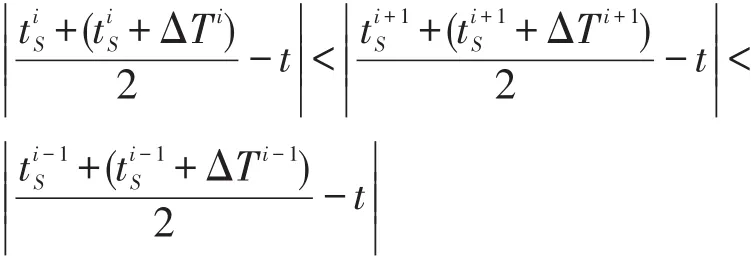
(2)非传播性系统拥堵量化模型.

针对非传播性系统拥堵，各条路段拥堵独立发生和消散，不具备传播特性，因此该类系统拥堵程度仅通过道路实时延时指数进行量化.具体量化模型为

(3)路网系统拥堵综合量化模型.

结合式(2)和式(6)的计算结果，考虑两类拥堵状态的拥堵路段数差异，建立路网系统拥堵综合量化模型为

3.3 路网系统拥堵极限状态确定

路网系统拥堵极限状态表示指定区域中整个数据获取时间段内拥堵情况最严重的状态，即所有时刻中路网系统拥堵综合程度最大的状态.将该状态对应的时刻记为tc，路网系统拥堵综合程度记为，则，其中t为集合Nmax出现当天历史数据中的任意时刻.

4 路网实时拥堵状态的识别

路网实时拥堵状态的量化是通过将当前时刻tr的路网系统拥堵状态与该路网系统拥堵的极限状态作比较，以实现tr时刻路网拥堵状态的快速识别.

路网系统拥堵各天具有相对稳定性，系统拥堵极限状态中的Nmax包含的所有路段，在任意时刻都会有动态的交通延时指数.对于存在传播性拥堵关系的路段集合，各相邻路段若采用与极限状态识别过程中相同时刻的权重值wa,u，全部路段根据式(2)可以有效还原tr时刻道路网络的运行状态；对于非传播性系统拥堵路段，可以根据式(6)计算tr时刻的拥堵程度；将两者相结合，根据式(7)即可计算出路网tr时刻运行状态的综合拥堵程度.

考虑路网实时拥堵状态与拥堵极限状态的拥堵程度和拥堵路段数两方面的差异，提出量化模型为

5 实例分析

5.1 基础数据准备

选取重庆市渝中半岛部分路网作为实例研究区域，其范围如图3所示.图中的数字表示研究区域的节点编号，带箭头的路段为单向道路，该区域共40个节点和77条路段(1条双向道路当作2条单向路段)，实例中将利用节点编号表示路段，例如节点i至节点j之间的路段表达成L(i,j).

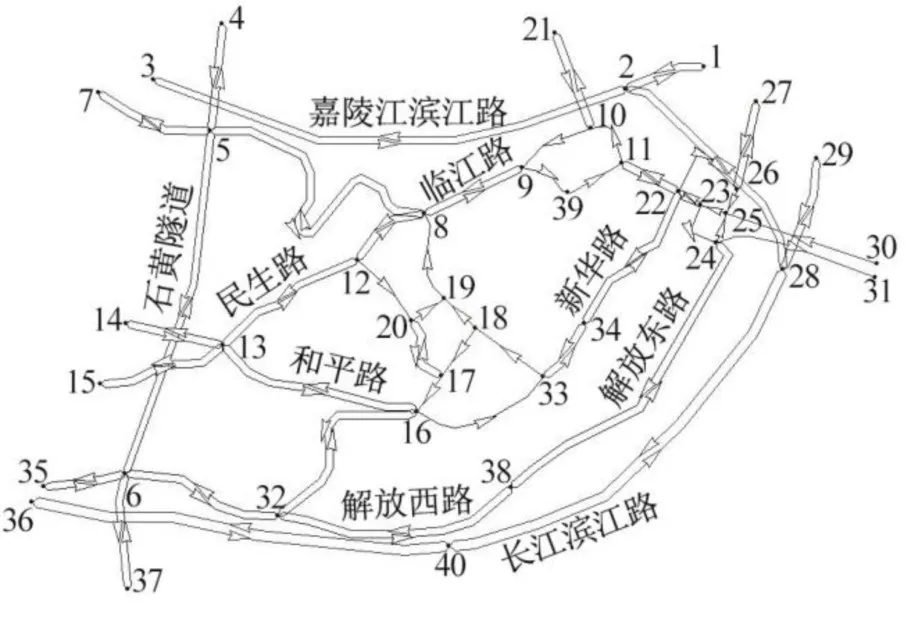
图3 实例研究区域Fig.3 Instance study area

通过自编Python程序自动爬取了一个工作日中上午6 h(6:00-12:00)的道路运行速度数据，爬取间隔为5 min，共计73个时刻(包括起始时间点和终止时间点).另外单独爬取了该区域第2天上午10:45的道路运行速度数据进行路网实时状态识别.

5.2 路网系统拥堵路段集合搜索

运用Matlab软件对前文所述的路网系统拥堵特征的识别算法进行了编程，并将其用于实例路网中系统拥堵路段集合的搜索，具体结果如图4所示.

图4 路网系统拥堵路段集合Fig.4 The system congestion section collection of road network

在图4中，加粗路段表示为系统拥堵路段，实例区域中的路段长度均较小，拥堵路段均为传播性系统拥堵路段，共有35对相邻系统拥堵传播路段，其路段总数为38条，在后续示例分析中直接将其涵盖的路段集合视为Nmax.

5.3 路网极限拥堵状态和实时拥堵状态的量化

根据已搜索的Nmax和路网系统拥堵程度的量化方法，通过Matlab自编程序分别计算出TNmax中各个时刻的相邻路段关联程度和路网系统拥堵程度，如图5所示，并从中找出路网系统拥堵极限状态对应的时刻点tc及拥堵程度值，其中tc=7:50(对应第23个时刻)，=4.39；然后计算出路网实时状态(即tr=10:45，对应第58个时刻)的系统拥堵程度值=3.56，具体计算数据如表1所示.

通过对tc与tr时刻各条路段的延时指数进行判断，两个时刻的道路拥堵条数分别为35条和37条，此时根据式(8)计算得路网实时拥堵状态与拥堵极限状态的接近度SD=0.86，由此可知tc与tr时刻拥堵状态较为接近.

图5 所有时刻的系统拥堵程度值Fig.5 The degree of system congestion at all times

表1 tc与tr时刻相邻路段拥堵程度计算表Table 1 Calculation table of congestion degree of adjacent sections for timestcandtr

6 结 论

本文以在线地图道路延时指数作为数据基础，提供了一种路网实时拥堵状态识别的全新方法.通过对路网系统拥堵特征的分析，构建了路网系统拥堵的量化方法，建立了路网实时拥堵状态与极限拥堵状态的接近度模型，有助于交通管理者根据拥堵程度制定实时的缓堵策略.

限于篇幅，本文未对系统拥堵特征中各个条件的阈值和路网实时拥堵状态的拥堵等级划分方法进行拓展研究，将在后期的研究中对上述两个问题进行完善，以便能更准确的识别路段拥堵特征和网络的运行状态.