浅谈“化复为实”思想在“复变函数”教学中的应用
杭 俊, 张 燕
(安徽大学 电气工程与自动化学院, 安徽 合肥 230601)
0 引言
“复变函数”不仅是数学专业的一门重要专业课,更是电气、自动化、通信等工科专业的专业基础课,这些专业很多的成果都以复变函数理论为基础。近几十年来,随着科学技术的迅猛发展,复变函数的理论与方法也不断得到扩充与完善,复变函数的理论与方法也越来越多地应用到工程实践中去,如流体力学、电磁学、热学和弹性理论等[1]。因此,学好“复变函数”课程对于在校大学生和科学技术工作者是十分重要的。教学质量的高低、教学效果的好坏直接影响到学生对这门课程以及后续课程的学习。因此,这就对“复变函数”课程教学提出了新的要求。
复变函数是在实变函数的基础上延伸出来的,它们的联系是很紧密的。复变函数中的许多理论、概念和方法是实变函数在复数域的推广,所以它的许多概念和性质与实变函数内容既有相同之处也有不同之处,它们的区别就在于前者是研究复数域上的函数,后者是研究实数域上的函数[2-5]。因此,这就要求在讲授“复变函数”课程时要充分利用“高等数学”课程中实变函数的思想和方法来进行教学。这样不仅可以提高学生学习的速度,而且能让学生把握复变函数课程的核心思想。这对学生系统地掌握复变函数的基本理论有很大的帮助,对提高“复变函数”的教学效果有着深远的影响。
笔者通过对电气工程专业学讲授复变函数这门课程,总结出一些有益的经验,让学生始终在大脑中有一个将学习复变函数的问题转化为实变函数的思想(简称“化复为实”思想),可有效地提高学生学习的效果。本文的后续内容将结合复变函数具体内容和案例说明如何将“化复为实”思想贯穿于整个“复变函数”教学和学习过程中去。
1 复变函数定义
设有一复数z=x+iy的集合G,如果有一个确定的法则存在:对于集合G中的每一个复数z,就有一个或几个相应的复数w=u+iv随之而定,那么称复数w是复变数z的函数,简称复变函数,记作w=f(z)[6]。
由于给定了一个复数z=x+iy就相当于给定了两个实数x和y,而复数w=u+iv也同样对应着一对实数u和v,所以复变函数w和自变量z之间一定存在某种关系。w=f(z)相当于两个关系式为

(1)
从式(1)中可以看出u和v皆伴随x和y而定。此时
w=f(z)=u(x,y)+iv(x,y)
(2)
式中:u(x,y)和v(x,y)为二元实变函数。
为了加深对复变函数和自变量两者关系的理解,举“复变函数”授课中常用的一个函数w=f(z)=z2为例说明。令z=x+iy,w=u+iv,那么
w=u+iv=f(z)=(x+iy)2
(3)
根据恒等式原理,等式两边实部与虚部分别相等,因此,根据式(3)可得
(4)
从式(4)可以看出,函数w=z2对应于两个二元实变函数。从这个结果可以初步地看出,研究复变函数的性质就转换到研究复变函数的实部和虚部的性质,而实部和虚部都是二元实变函数。因此,归结为就是利用实变函数来研究复变函数。下面将就复变函数研究的内容来更进一步阐述这一思想(将复变函数问题转化为实变函数问题),由于复变函数涉及的内容很多,本文就选取几个方面来阐述这种思想,主要包括复变函数的极限、解析函数、复变函数的积分和级数。
2 复变函数极限
关于极限有如下定理:
定理设f(z)=u(x,y)+iv(x,y),A=u0+iv0,z0=x0+iy0,那么limf(z)=A的充要条件是

x→x0x→x0
y→y0y→y0
可以清楚地看出,这个定理将求复变函数f(z)=u(x,y)+iv(x,y)的极限问题转化为求两个二元实变函数u=u(x,y)和v=v(x,y)的极限问题。为了加深对这个定理的理解和应用,举例说明。

证令z=x+iy,则


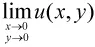
3 解析函数
关于解析函数有如下定理:
定理函数f(z)=u(x,y)+iv(x,y)在其定义域D内解析的充要条件是:u(x,y)与v(x,y)在D内可微,并且满足柯西-黎曼方程
(5)
从定理可以清楚地看出,这个定理将求复变函数f(z)=u(x,y)+iv(x,y)的解析问题转化为求两个二元实变函数u=u(x,y)和v=v(x,y)的可微问题并且微分满足一定的关系。为了进一步说明这个定理,举例说明。
例设函数f(z)=x2+axy+by2+i(cx2+dxy+y2)。问常数a, b, c, d取何值时,f(z)在复平面内处处解析?
解由题可知
u=x2+axy+by2v= cx2+dxy+y2
根据实变函数的理论可知,u和v在整个平面内处处解析,所以
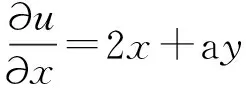
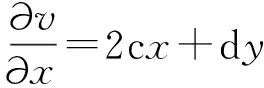
从而,要使f(z)在复平面内处处解析,还需要满足柯西-黎曼方程,即
只需要2x+ay=dx+2y, 2cx+dy=-ax-2by。因此,当a=2, b=-1, c=-1, d=2时,此函数在复平面内处处解析。
从定理和例子可以看出,在研究复变函数f(z)=u(x,y)+iv(x,y)的解析问题时,其实就是转化为求两个二元实变函数u=u(x,y)和v=v(x,y)的可微问题,然后再利用实变函数理论进行解决。
4 复变函数积分

1. 用两个二元实变函数的线积分来计算

(6)
2. 当光滑曲线C由参数方程
z=z(t)=x(t)+iy(t)ta≤t≤tβ
(7)
给出时(正方向为参数增加的方向,参数tα及tβ对应光滑曲线的起点和终点,并且),复变函数的积分可计算为

(8)
由式(6)和(8)可以看出,不管用哪种方式求复变函数的积分,归根到底都要转化到求实变函数积分的问题。下面举例进一步说明这种思想。

解此例题采用第二种方式,采用第一种方式同样可以求解。
直线段C的方程可写作:
x=3t,y=4t,0≤t≤1
在C上,z=(3+4i)t,dz=(3+4i)dt。于是
从上述计算过程可以看出,求复变函数的积分就是转化到实变函数求积分的问题。
5 级数
5.1 级数
设{αn}={an+ibn}(n=1, 2…)为一复数列,表达式为

称为无穷级数。
关于级数收敛有如下定理:
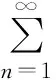
可以看出该定理将复数级数的收敛问题转化为实数项级数的收敛问题。下面通过例题进一步说明这种思想。

解由级数可知
发散
收敛
故原级数发散。
5.2 幂级数

从上述两个定理可以明显地看出,求解幂级数的收敛半径其实还是求实变函数极限的问题。下面通过例题进一步说明这种思想。

解1)用比值法计算

所以收敛半径R=1,也就是原级数在圆|z|=1内收敛,在圆外发散。
2)用根值法计算
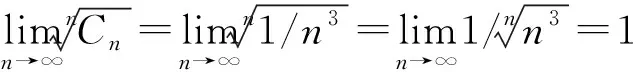
所以收敛半径R=1,也就是原级数在圆|z|=1内收敛,在圆外发散。
可见,用两种方式求的收敛半径是相等,并且在求解过程中其实都是在求实变函数的极限问题。
因此,综述上述内容,从复变函数定义、复变函数极限、解析函数、复变函数积分和级数可以充分地看出,在解决复变函数问题都是将其转化到实变函数问题,再利用实现函数的理论进行解决。
6 结语
“复变函数”是“高等数学”的后续课程,是在实变函数的基础上延伸出来的一门课程。笔者根据讲授“复变函数”的经验,探索了将“化复为实”思想融入到复变函数的整个教学过程。本文从复变函数定义、复变函数极限、解析函数、复变函数的积分和级数等角度阐述“化复为实”思想其实是贯穿于整个复变函数教学和学习过程中的。在“复变函数”教学过程中,传递这种思想,可以提高学生的学习速度,能让学生把握复变函数的核心思想以及与实变函数的关联性。从而培养学生利用已有知识学习新知识的能力,进而提高学生的学习能力。

