“自动控制原理”课程学科特色及数学意义

潘玉民， 黄成玉， 邓永红

(华北科技学院 电子信息工程学院， 北京 101601)

0 引言

“自动控制原理”课程是一门具有跨学科特点且与哲学方法论密切相关的独具特色的学科课程。该课程渗透到航空、宇航、电力系统、通信、电子信息、数学、计算机、机电、管理工程等诸多专业，甚至涉及到经济学、社会学的控制等。因此，该课程的研究问题的思维及方法具有普遍的科学意义。

自动控制原理(或理论)是控制论学科和智能控制的基础，人工智能AI(Artificial Intelligence)的核心思想即源于此，人工智能目前是业界的一个研究热点。

自动控制的基本思想是使机器或设备具有人类似的功能与智能，即不需要人类的干预就能自动完成指定的任务，机器人就是最典型的实例之一。自动控制的价值在于使机器具有类似人脑的思维能力，譬如反馈就是一个反映思维能力的标志性概念。一个决策是否可行，将最初的想法与执行之后的实际结果进行比较产生偏差，即反馈过程。反馈是生命的核心特征，也是思维的本质。从细胞蛋白质的相互作用，到复杂生态系统中生物体之间的相互作用都有它的贡献[1]。如果没有达到预期目标，由人设法调整、修改和完善，这一功能即“自动控制原理”中的控制器或者称为调节器的作用。通过不断反馈修正达到预期目的就是自动控制的过程，形成一个闭环控制系统，如图1所示。

图1中，执行机构有驱动放大作用，被控对象可以是电机、机器人以及其他对象，传感器完成信息采集任务。

图1 典型单闭环控制系统

自动控制理论的发展初期是以反馈理论为基础的自动调节原理。反馈系统是来源于生物学，自然界中，生物系统就是通过反馈来维持温度、化学条件以及生物条件的动态平衡[2]。在工程领域，反馈控制的典型实例是1769年詹姆斯·瓦特发明的飞球离心调速器，随着生产和科学的进步，该技术已发展成为一门独立的学科——控制论。广义而言，控制论是指把自动调节、通信工程、计算机技术以及神经生理学和病理学等学科以数学为纽带相互渗透形成的新型学科[3]。控制论跨越了自然科学和社会科学的界限，既研究自动工厂、学习机和智能机器，又研究经济、社会系统，探索怎样使这些复杂系统按照人们的期望去工作[4]。

控制论奠基人是美国科学家诺伯特·维纳，同时也是一位杰出的数学家，他对数理逻辑、概率论、调和分析等领域做过十分重要的研究。然而，维纳一生中最辉煌的时期是1940～1947年间他对火力控制的研究。1948年维纳出版划时代的著作——《控制论》，标志着控制论这一崭新学科诞生。

1 自动控制理论的方法论特色

1.1 自动控制理论主要方法概述

基于自动控制理论的方法论特色及意义主要体现在以下几个方面[5]：

(1)根轨迹法：利用作图法解决数学高次方程求解问题，建立开环系统与闭环系统的联系，不必解方程即可分析闭环系统特征根的情况，从而分析系统的全部性能。高次方程求解至今仍是数学没有解决的问题，而控制系统分析归结为求根问题，因此根轨迹法是对数学的重要贡献。从系统响应角度分析，根轨迹也属于时域法。

(2)频域法：利用正弦稳态响应特性，同样不用求解高次方程，利用图解法绘制波特图、奈奎斯特曲线等即可分析系统的所有性能。

(3)时域法：该方法是一种直接在时间域中对系统进行分析的方法，具有直观、准确的优点。

(4)结构图、信号流图方法：通过绘制结构图化简即可解微分方程组求传递函数，不必化简信号流图即可直接求出系统的传递函数，这是控制系统非常重要的工作。

(5)赫尔维斯判据、劳斯判据：不经求解高次方程，只用高次方程的系数组成行列式或劳斯阵列即可判别系统的稳定性，其中劳斯判据还能指出有几个不稳定根。奈奎斯特判据只需知道开环传递函数，通过绘制奈氏曲线即可判别系统的稳定性。

(6)李雅普诺夫稳定性方法：通过构造能量函数判别系统的稳定性等。

(7)黑箱辨识方法：通过观测输入黑箱的信息和输出信息的变化关系，探索黑箱的内部构造和机理的方法。这是一种系统建模方法，如炼钢炉温度控制系统，很难写出其数学方程式，但可以通过燃料量控制炼钢炉的温度，记录温度响应曲线，然后用近似模型逼近曲线达到建模的目的。智能控制中的人工神经网络就是最典型的“黑箱”分析的方法。

“黑箱”是指内部构造和机理不能直接观察的事物或系统，该方法注重整体和功能，兼有抽象方法和模型方法的特征。维纳认为“对于控制系统，不管其组成如何，均可通过黑箱方法进行研究。”

(8)相似系统方法：如图2(a)和图2(b)分别是RLC电路网络和弹簧—质量—阻尼器机械系统。

两个系统的微分方程(即数学模型)为

(1)

(2)

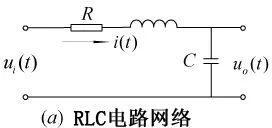
图2 相似系统

从图3及数学模型可以发现，物理结构不同的元件或系统，可以具有相同形式的数学模型，RLC无源网络和弹簧—质量—阻尼器机械系统的数学模型均是二阶微分方程，称之为相似系统。如果方程的系数在数值上取成相同，则两个系统本质是相同的。

相似系统揭示了不同物理现象之间的本质相似关系，利用相似系统原理用一个简单系统研究与其相似的复杂系统。相似系统为控制系统的计算机数字仿真技术奠定了基础。

1.2 基于信息论角度描述控制系统

笔者认为任何一种控制过程，其基本思想均可从信息论角度加以认识和概括，无论是生物界还是电气、机械自动化等系统，包括人类思维过程、自然界的自动控制，均可以认为是信息的测量、获取、传递、比较、处理和执行的过程，如图3所示。图中信息处理机可以是计算机，也可以是人脑的思维过程及具有处理能力的功能体。

从哲学视角，对“信息”目前尚无统一定义。一般认为，信息是事物及其属性标识的集合，是物质、能量、信息及其属性的标示。

图3 信息处理系统

从图3可以看出，一个控制系统本身具有信息论、控制论、系统论的特征。信息处理部分起控制和调节作用，体现调节规律；反馈部分属于通信范畴，即信息论应完成的任务，也可以是远程控制或遥控，如航空航天控制；图4本身就具有一定的智能，不需要人来干预的有机的自动控制系统，因此必然有系统论的特点。因此，自动控制系统是“三论”的融合体现，如图4所示。

图4 “三论”与控制系统的关系

系统论认为，在合理配置的前提下，系统功效大于局部功效之和。系统论的一则实例：前苏联研制的“米格—25”战斗机，被认为是曾经创造过神话的一代战机[6]。该型战机之所以具有高超的性能，并不在于前苏联开拓了什么高新的技术领域，而是成功地利用了系统理论的整体功能原理，将并不是最先进的众多元件加以高效的有机整合，从而产生了惊人的系统效果。

1948年，奥地利出生的美国生物学家贝塔郎菲出版了《生命问题》一书，描述了系统思想在哲学史上的发展，确立了适用于系统的一般原则，标志着系统论这门新型的逻辑和数学领域科学的诞生。同年，美国贝尔实验室香农博士发表了信息论的奠基性论文——《通信的数学理论》，旨在解决通信的两个基本问题：信息传递的有效性和可靠性，标志着一门新的学科──信息论的诞生。香农对信息的概念加以简化，并用比特作为量纲衡量后，人们发现信息几乎无处不在。

但目前信息论的意义和应用范围已超出通信的领域。自然界和社会中有许多现象和问题，如生物神经的感知系统、遗传信息的传递等，均与信息论中研究的信息传输和信息处理系统相类似。因此信息论的思想对许多学科如物理学、生物学、遗传学、控制论、计算机科学、数理统计学、语言学、心理学、教育学、经济管理研究等都有一定的影响和作用。

2 课程与数学的关系

“自动控制原理”课程与数学联系密切。控制理论学科，通常被视为一门应用数学学科，它的基本工具和手段是数学的理论与方法。如高等数学、复变函数及线性代数等是自动控制理论发展的重要基石。建立在微积分和复变函数与积分变换引出的数学模型、传递函数；时域到复数域的数学转换；基于线性代数和微分方程的状态空间分析法；基于变分法的最优控制等。可以说，现代数学贯穿控制理论学科发展的全过程，对控制理论的发展具有决定性的作用。但是，控制理论反过来又发展了数学，并且在数学上有独到和创造性突破。

现代数学与控制理论的密切联系还体现在一些高校数学系开设自动控制专业，如南开大学、山东大学等。南开大学于1984年将原数学系自动控制专业与其他专业整合，经过几轮调整为目前的计算机与控制工程学院；50年代初山东大学数学系开设控制理论专业，目前已发展为山东大学数学学院的运筹学与控制论专业，该专业目前开设“自动控制原理”、“线性系统理论”、“最优控制”等课程。

此外，一些数学家本身就是控制理论专家，如诺伯特·维纳，俄国数学家李雅普诺夫1892年创立的控制系统稳定性理论；英国数学家劳斯和德国数学家赫尔维茨各自提出直接根据代数方程系数判别系统稳定性的准则；1956年，美国数学家贝尔曼提出了离散多阶段决策的最优性原理，创立了动态规划理论，之后，贝尔曼等人提出了现代控制理论的状态空间分析法等。

3 课程的图形化特色

“自动控制原理”课程的一个显著特色是以“图”为特征并贯穿课程始终。图形化方法将数学的抽象问题变成平面或立体化问题。具有直观、简单以及能更深刻地揭示其内在规律的特点。

在自动控制系统的分析与设计中，图解法起着十分重要的作用。如结构图、信号流图、时域响应曲线，根轨迹图、波特图、奈奎斯特曲线、相轨迹图、状态变量图等图形化特征，也是有别于其他课程的独到之处和亮点所在。自动控制原理各种图形化如图5所示。

此外，还有尼科尔斯曲线、负倒描述函数曲线等。以图形为主线展开的“自动控制原理”课程，必然呈现出形象直观和易懂的特点。

图5 自控原理的图形化特征

1)图形化的教学意义

从课程教学角度出发，图形化可使教学内容形式表现为形象直观，易于实现平面化、立体化教学，尤其符合思维与认知规律，可使抽象、枯燥的教学内容、数学理论富有生命力，引起学生兴趣，大大增强教学效果。法国哲学家、数学家笛卡尔指出：“没有任何东西比几何图形更容易印入脑际了，因此，用这种方式来表达事物是非常有益的。”美国数学家斯蒂恩认为：“如果一个特定的问题可以转化为图形，那么，思想就整体地把握了问题，并且能创造性地思索问题的解法。” 控制理论的图形化思想不仅实现直观教学，由浅入深，同时对数学理论及控制理论都具有深远意义。图形化可以引发许多新的发现和理论的创造性突破。

图解法使“自动控制原理”课程内容丰富多彩，呈现直观、易懂的特点，同时是一种解决科学问题的有效方法。根轨迹法将高次方程求解转化为几何作图问题，在笛卡尔直角坐标系绘制根轨迹，通过作图法则间接求出高次方程的根，同时又能分析控制系统的稳定性、稳态精度和动态性能；频域法是利用开环传递函数绘制波特图，即可间接分析闭环控制系统的动、静态性能，不必解出高次方程的根即可分析系统，波特图和根轨迹图均可以提供控制系统的全部信息。基于频率法的奈奎斯特稳定判据，根据奈氏曲线绕(-1，j0)点的圈数即可判别闭环特征方程根的情况。因此，控制理论中图形化的方法已远远超出形象、直观层面的教学意义，而对控制理论具有杰出的贡献。

显然，若能挖掘问题的几何意义，附以图形就能取得以简驭繁的效果。采用图形化研究解决数学问题、控制理论问题符合认知规律，同时可以有新发现。图形化方法给抽象的数学问题注入了活力。

2)“自动控制原理”课程与Matlab软件

值得指出的是，当今流行的Matlab软件，是由美国Mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全新的解决方案。

Matlab有极强的图形绘制、设计及大数据处理能力，对“自动控制原理”课程教学与学生的课程学习提供了强有力的支撑，可谓是一条“教”与“学”的快速通道。利用Matlab软件强大功能可加深对课程内容的理解，可起到事半功倍的作用，使数据及图形绘制精准、高效，而且很容易掌握及付诸实践。Matlab特别是擅长于矩阵运算，因此，对现代控制理论学习，以及各种图形绘制方便、快捷，可以大大提高教学和学习的效率及深度。

笔者在讲授“自动控制原理”课程时，充分利用该软件进行教学，取得了较好的效果。利用Matlab软件绘制控制原理的根轨迹、波特图、时域响应分析等十分方便，可以动态显示所有参数变化情况，以及方便地获取系统参数的具体数值，还可以根据性能指标要求进行系统设计。

4 学科课程之间的内在联系与发展

辩证法的世界观要求从事物的普遍联系和永恒运动中把握事物。大千世界，事物之间存在普遍联系，是矛盾的对立统一体。牛顿1687年出版的《自然哲学的数学原理》中提出了著名的万有引力定律，指出万有引力不仅是天体中星体之间的相互联系的特征，也是所有物体相互吸引作用的特征。爱因斯坦的广义相对论是一种关于万有引力本质的理论。量子力学是微观粒子遵循的普遍规律，量子纠缠与相干性是粒子组成的系统中相互影响的现象，即使相距遥远距离，一个粒子的行为将会影响另一个粒子的状态。混沌理论中的“蝴蝶效应”是指初始条件十分微小的变化经过不断放大，对其未来状态会造成巨大的差别，表征了事物之间的联系、影响及不可预测性。

值得指出，智能控制理论是控制理论的最高层次，智能控制中的核心技术是模糊理论、神经网络和专家系统。而智能控制、人工智能均以人脑智能为参考体系和模拟的对象。模糊数学在控制工程中的应用产生了模糊控制，神经网络理论与控制理论的结合产生了神经网络控制。模糊理论和神经网络技术是近几年来人工智能的研究热点。

笔者认为，人工智能的核心在于人脑的功能和智慧的模拟，人脑是一个极为精巧和完善的信息处理系统。从哲学角度人脑是一个高度复杂的巨型系统，有奇异的思维能力，现象神秘莫测,需要哲学、认知科学、神经生理学、心理学、计算机科学、信息论、控制论等多学科进行研究。

模糊神经网络技术是人工神经网络和模糊逻辑有机结合的产物，属于交叉前沿学科。兼有神经网络与模糊理论的优点，彼此优势互补，集学习、联想、识别、信息处理于一体，被认为是21世纪的核心技术。神经网络与模糊理论这两个方向有着天然的内在联系：人工神经网络相当于是对人脑神经系统“硬件”的模拟，模糊逻辑类似对人脑思维“软件”的模拟，本身就是对同一对象两个侧面的模拟，二者结合才能构成一个完整的有机体系。不仅如此，遗传算法、免疫功能等也是人体的基本功能，因此，有基于遗传算法的神经网络、遗传算法优化模糊控制、免疫神经网络等研究方向。因此，各学科课程协同发展，彼此加强，是产生新型交叉学科、促进科学发展的动力，学科交叉研究体现了科学向综合性发展的趋势。

由此可见，不同学科相互协作，相互融合，更容易取得突破性进展。通透学科之间的壁垒，促使各学科彼此渗透，交叉学科具有很强的生命力。

5 结语

“自动控制原理”课程具备与其他学科课程的兼容性，且图形化及方法论特色鲜明，尤其与现代数学联系紧密。从哲学角度来看，揭示事物间的普遍联系，促进学科课程的整合，开阔视野，使各学科广泛联系，协同发展，既为科学研究注入活力，又能为高校教学提供可持续发展的动力，使教学成效产生质的飞跃。

再进一步，使课程的教学与 “慕课”、“微课”、“翻转课堂”等相应的教学模式融合，促进信息技术与课程的深度融合，对教学的内涵发展更是大有裨益。