基于发射功率自适应的无人机图传系统节能方法*

王帅凡, 曾国辉, 吴 迪, 赵 威, 黄 勃, 韦 钰

(上海工程技术大学 电子电气工程学院，上海 201600)

0 引 言

微小型无人机(unmanned aerial vehicle,UAV)在航拍、电力监测等诸多领域广泛应用[1]，其主任务之一是获取图像信息并传输[2]。目前微小型无人机存在一个亟待解决的问题,即续航时间短[3，4]。对此，国内外许多研究主要集中在总体参数优化和动力系统优化两方面。如文献[5]中利用遗传算法对无人机总体参数进行了优化；文献[6]通过建模分析对无人机动力系统进行了优化。

随着图像质量和传输距离上升，无人机图像传输系统能耗相应上升，文献[3]指出航拍无人机用于图像传输的电能占无人机总电能的20 %。因此,由图传系统对无人机进行节能具有研究价值。现有产品中，无人机图传发射机的发射功率多为恒定，文献[7，8]提出利用发射功率自适应方法可有效降低发射机能耗，发射功率自适应也符合无人机情景感知和智能控制的发展要求[9，10]。本文据此提出利用发射功率自适应方法对无人机图传系统进行能耗优化。

1 数学建模

无人机图传系统一般由发射机和接收机两部分组成，发射机固定于无人机，由无人机供电，接收机用于地面接收，由地面电源供电。从无人机能耗角度出发，无人机图传系统单指图传系统的发射机部分。发射机的能量消耗主要来自于两部分：基础工作电路和射频放大电路，基础工作电路用于前期的信号处理，工作功率相对稳定；射频放大电路将前期信号转换为射频信号并放大发射，主要由射频功率放大器组成，原理是将直流输入功率转换为射频输出功率。本文所述发射功率指射频输出功率。在转换效率固定时，射频输出功率的变化会引发直流输入功率的变化，使无人机图传系统的整体工作功率发生变化。因此，图传系统的发射功率若能根据工作情境自适应调节，就能适时改变直流电源的输入功率，从而帮助图传系统进行能耗优化。

目前关于无人机图传发射功率的数学模型不多，本文优先建立一个关于发射功率的数学模型。发射功率由路径损耗和接收灵敏度决定，在灵敏度确定的情况下，路径损耗决定了最佳发射功率，亦即本文发射功率自适应调节的理想值。故本文从路径损耗、接收灵敏度模型入手建立理想发射功率模型。

1.1 路径损耗模型

选取Okumura-Hata模型[11]作为发射功率模型的参考模型之一，其标准公式为

(1)

式中PN为信号的路径损耗，dB；fc为传输频率,MHz，范围150～1 500 MHz；hf为天线有效高度,m，在无人机上可近似表示为飞行高度，范围20～200 m；hs为接收天线有效高度m，范围1～10 m；α(hs)为接收天线修正因子；D(范围1～20 km)为发射端到接收端的距离,km。

1.2 接收灵敏度模型

接收灵敏度模型主要参考文献[12]中的公式

(2)

式中Sr为接收灵敏度，dBm；B(Hz)为传输带宽,范围为1×106～8×106Hz；NFf为射频前端噪声系数；G为射频前端增益;δ为监测信噪比；NFAD为A/D的噪声系数

NFAD=174+PFS(dBm)-SNR(dBFS)-10lg(Fs/2)

(3)

式中PFS(dBm)为 A/D 满量程输入功率，SNR(dBFS)为A/D 信噪比，Fs为采样频率。

由式(2)、式(3)可以看出,影响接收灵敏度的因素中与接收机选择的具体芯片有较大关联，一旦芯片选定，大部分参数值即确定。参考文献[12]中的典型芯片取值，NFAD取45 dB；NFf取3.1 dB；G取45 dB；δ取0，从而简化接收灵敏度模型为Sr=-169.23+10lgB。

1.3 理想发射功率模型

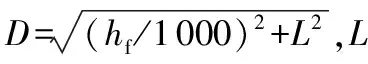
Pf=-99.72+26.16 lgfc-13.82 lghf+10 lgB+

(4)

2 自适应方案分析

由式(4)可以看出，影响图传发射功率的主要自变量有fc,hf,B,L。为确定功率自适应参考标准，本文采用控制变量法分别计算4个变量对发射功率的影响程度。

1)当fc为自变量，取hf=100 m，B=6×106Hz，L=10 m，关系如图1(a)所示；

2)当hf为自变量，取fc=300 MHz，B=6×106Hz，L=10 m，关系如图1(b)所示；

3)当B为自变量，取fc=300 MHz，hf=100 m，L=10 m，关系如图1(c)所示；

4)当L为自变量，取fc=300 MHz，hf=100 m，B=6×106Hz，关系如图1(d)所示。

图1 各变量与发射功率关系

由图1可以看出，在取值范围内，水平传输距离L影响力最大，且在工程中的频率、带宽往往被客户直接要求，自身变化范围有限；水平距离和飞行高度多为连续变化，但飞行高度受国家政策和动力系统等条件限制，同时影响力低于水平距离，所以,选取水平传输距离L作为发射功率自适应的参考标准。即确定本文的功率自适应方案为以水平传输距离作为参考标准，调节发射功率，使两者合理匹配，在传输距离变小(变大)时降低(增大)发射功率，达到节约能量的目的。

3 算例分析

3.1 计算原理

射频功率放大器的本质是将直流功率转换为射频功率[13]，其自身功率主要由效率和输出功率决定，其效率为η=Po/Pdc，Po为射频功放输出功率，对应上文所述发射功率Pf,Pdc为直流功率，对应无人机电池的输出功率。可知，在射频功放效率一定的情况下，Pdc会随Po变化而相应变化，这是功率自适应节约电能的关键。

计算图传系统能耗需要计算射频功放能耗，在输出功率(发射功率)已知的情况下，功放效率尤为重要，但功放效率会随器件变化。经过对现有图传发射终端功放效率调研，获得相应数据并通过最小二乘法拟合得到输出功率与功放效率间近似关系为

ηc=0.004PF+12.48

(5)

式中ηc为通过拟合函数计算得出的功放效率，%；PF(nW)为输出功率，对应上文中的Pf。

至此，基本模型建立完成，开始进行自适应节能效果计算。由于以水平传输距离L作为发射功率自适应的参考标准，在计算中仍旧取频率fc=300 MHz，飞行高度hf=100 m，传输带宽B=6×106Hz。由不同的L经式(4)可以求得不同的发射功率Pf，由式(5)，求得对应的功放效率，根据工作时长便可计算出图传系统发射端的电能消耗量Ez(W·h)

Ez=(Pf/ηs+600)/1 000×t

(6)

式中ηs为对应的功放效率；600为发射电路板基础功率，mW；t为工作时长，h；Pf需要格外注意，由式(4)计算出的Pf单位为dBm，要转换为mW单位，转换公式为Pf(mW)=10Pf/10。

3.2 结果分析

参考文献[14]制定两种无人机航拍方式，并分别计算自适应图传发射系统的节能效果。

1)假设飞行最远水平距离为3 km，分别在距接收点水平距离1，2，3 km处设置3个固定拍摄点，每个拍摄点规定3 min的悬停拍摄时长，其他飞行时段图传系统不工作。

a.非自适应模式下，为保证最远传输距离时能接收到信号，通常按照最远距离3 km来设置发射功率，即以3 km时的发射功率工作9 min，经计算电能消耗量为0.222 W·h。

b.自适应模式下，分别在1,2,3 km处以不同的发射功率工作，经计算1，2，3 km处的电能消耗量相加，计算结果如表1所示。

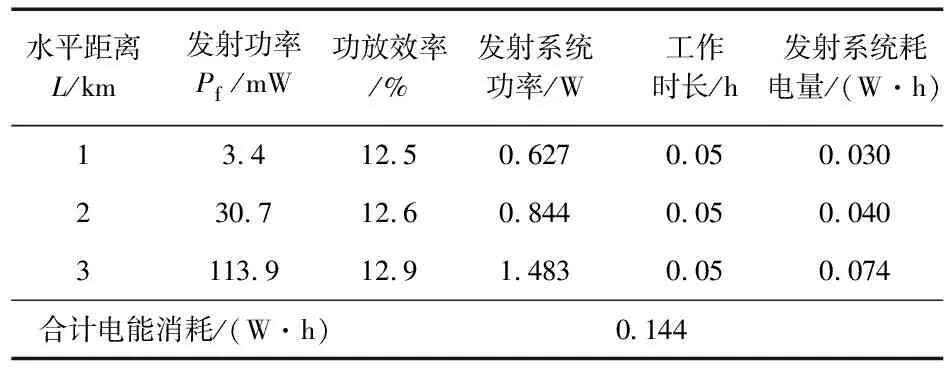
表1 方式(1)下自适应发射系统耗电量数据表

由结果可以算出，此种航拍方式下，采用发射功率自适应以后，完成相同任务，节约了原电能的35 %。

2)假设无人机飞行全程均在拍摄，拍摄时长 30 min，最远水平距离5 km。

a.非自适应模式下，按照最远距离5 km来设置发射功率，即以5 km时的发射功率工作30 min，经计算电能消耗量为2.2 W·h。

b.自适应模式下，先将5 km以1 km为步长分为5个梯度进行功率自适应(较低精度的自适应方式)，按照无人机匀速飞行计算，每6 min飞行1 km，每1 km内以同一发射功率工作，计算每1 km的电能消耗量相加，计算结果如表2。

表2 方式(2)下低自适应精度发射系统耗电量数据

由结果可以算出，在此种工作方式下，采用较低精度的发射功率自适应后，完成相同任务，节约了原电能的54.5 %。同时，对比表1和表2可发现，随着最远传输距离的上升，节电量比例也在上升。

同样在方式(2)下，考虑增加自适应精度，将5 km以0.5 km为步长分为10个梯度进行功率自适应，每3 min飞行0.5km，每0.5 km内以同一发射功率工作，其他假设不变。计算结果为0.894 W·h。(说明，由于0.5 km不适用于式(4)，所以0.5 km处仍然以1 km计算)。

由结果看出，采用较高精度的发射功率自适应后，节约了原电能的59.5 %；相较于较低精度的发射功率自适应方式，也节约了约10.6 %的电能。

4 结 论

结合Okumura-Hata传播模型和接收灵敏度模型可以建立一个无人机图传系统的理想发射功率模型。以传输距离作为参考标准的发射功率自适应方案可以有效降低无人机图传系统的能耗。3～5 km内的功率自适应调节，可节省原发射系统30 %以上的能量，且伴随自适应精度和最远传输距离的增加，节能效果提升。但本文中发射功率模型是在Hata模型的基础上建立，覆盖范围不足；同时，在接收灵敏度模型和可调参数上进行了一定程度的简化，模型精度有待完善。在后期研究中，图传系统的能耗优化模型应结合无人机动力系统进行更深入的研究。