基于数值仿真的双马达同步耦合模型*

杨宜坤， 徐信芯， 田文鹏

(长安大学 工程机械学院，陕西 西安 710100)

0 引 言

目前传统振动压路机[1]主要依靠单个马达或双马达通过同步装置实现偏心块的回转运动，而这种结构普遍存在着单个振动马达因长时间使用而故障、振动同步装置齿面易损坏和双偏心块安装精度要求高，检修困难等问题[2]。本文设计了一种新型振动压路机钢轮振动模型——无同步装置的双马达振动系统，根据耦合理论，实现双马达带动偏心块的同步振动。液压马达同步即转速相等，而由于各自结构的细微差异，使其高压、高转速下内泄漏和阻力存在巨大差异，成为影响两马达同步运动的主要因素。传统方法解决同步问题均为加入齿轮同步装置或同步分流阀，而直接从内部结构方向开展同步研究处于国内外空白[3]状况。

传统振动压路机振动轮工作装置一般只有1个马达，其存在的问题也很凸出，如单马达适应工况能力差、激振力不足等问题，本文在前人设计的基础上，创新性地提出了双马达振动钢轮系统，2个马达可以选择性地交替工作也可同时工作，弥补了单马达适应性差，能耗利用率低的问题。目前，多马达驱动装置一般通过齿轮汇流来达到动力的传递，解决了因为马达转速差而导致的卡齿等现象，国内鲜有人直接从马达内部结构角度出发解决双马达同步工作问题。张宁[4]针对180吨大型矿用自卸车提出由双发动机、多马达联合驱动的思路，研究了多马达液压同步驱动方案的优劣，并进行了仿真分析。闻邦椿[5]对机电系统自同步理论进行了深入研究并取得了广泛应用。韩清凯等人[6]对系统同步过程中的稳定性和分岔理论进行了研究，但研究对象是机电传动而非液压传动。

本文通过马达内部结构差异性的分析，建立双马达耦合模型，从马达内部出发解决差速问题，进一步为其他领域多马达同步解决方案提供参考。

1 双马达振动钢轮的设计

针对无同步装置双马达驱动问题，本文设计方法如图1。

图1 新型双马达振动钢轮方法

2 双马达同步耦合理论

双马达驱动装置主要由双马达偏心回转机构、偏心块、地基组成。液压马达的流量由电比例流量阀调节，液压马达直接带动偏心快进行回转运动，两个马达采用对称布置，共同带动钢轮进行激振作业。通常，这种方案因为两个液压马达内部差异，比如泄露不同，回转阻力不同等，两个偏心块不会同步运动，导致钢轮无法正常工作，但由于两个回转运动之间存在着耦合作用，在同样的负载压力作用下，必然存在一个过渡区间，使得相位落后的偏心块所受的加速度高于相位超前的偏心块，相位超前的偏心块“拖”着相位落后的偏心块运动，直到两偏心块转速最后趋于一致，加速度一致，两个回转系统处于从过渡状态变为稳定状态，这就是双振动马达实现耦合同步振动的物理基础。

3 双马达耦合理论模型的建立

3.1 钢轮的运动微分方程[7]

假设：1)回转系统视为一个均质刚体；2)只考虑垂直方向的振动过程，水平方向的侧振和扭振忽略不计；3)两偏心质量块和偏心半径完全一致,忽略制造差异。通过对两回转系统运动学与动力学分析，建立模型如图2所示。

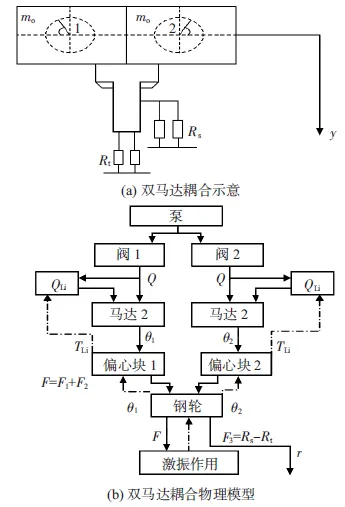
图2 双马达耦合模型

钢轮的运动微分方程为

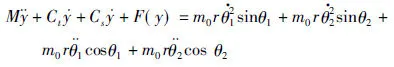
(1)

F(y)=Rt+Rs

(2)

式中M为钢轮系统总质量(包括钢轮质量)，m0为偏心块质量，y为钢轮系统垂直方向的位移，r为偏心半径，θ1,θ2分别为两偏心块的角位移，F(y)为激振力，Ct,Cs分别为轮侧和轮底的阻尼系数。

3.2 振动马达运动微分方程

如图2所示，新型钢轮分别由两个液压马达驱动偏心块回转。马达的输出扭矩包括负载和偏心块的摩擦以及惯性，其回转系的振动的微分方程为

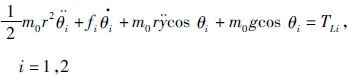
(3)

式中fi为马达两回转轴系的阻尼系数，TLi为两液压马达的有效力矩。

3.3 振动马达的泄漏方程[8]

马达容积损失的主要因素包括柱塞副的泄漏，配流盘和滑靴的泄漏，即

Qli=Ql1i+Ql2i+Ql3i

(4)

马达柱塞副在出厂加工时存在一定的配合间隙，当钢轮开启振动时，液压马达的柱塞副环形缝隙两端压差急剧上升，高压油通过环形缝隙流入低压壳体内，产生大量泄漏。

马达柱塞副泄漏流量方程为

(5)

(6)

式中d为柱塞的直径，δ1为柱塞副的间隙值，η为液压油的动力粘度，ε为柱塞的偏心率，PLi为马达负载压力，θi为柱塞随马达转过的角度，l为柱塞与柱塞副的接合长度，D为柱塞的分布圆直径，v为柱塞相对于柱塞孔的运动速度，α为马达斜盘的倾角，滑靴副泄漏方程为

(7)

式中δ2为滑靴副的油膜厚度；R1，R2分别为滑靴及通油孔半径值；λ为供压比，设为1。

配流盘泄漏方程为

i=1,2

(8)

式中δ3为配流副的油膜厚度；R5～R8分别为配流盘内外密封带半径；φ1,φ2分别为配流盘静压支承的有关角度。

4 双马达耦合模型的仿真分析

由上述公式可看出，就液压系统本身而言，马达的角位移和转速不仅与马达的内部参数(运动副缝隙和油液粘度变化)和输入流量相关，还与马达的负载扭矩相关，而马达的负载又与钢轮结构以及地面作用力相关。因此，振动钢轮的工作过程就是激振作用、机械系统和液压系统相互耦合并在一定条件下实现同步振动的过程。本文选用MATLAB/Simulink软件对运动方程式进行数值仿真[9,10]，仿真参数以华德HDA2FE80W61A11斜轴式柱塞马达为例，相关参数如表1。

表1 振动钢轮部分相关参数

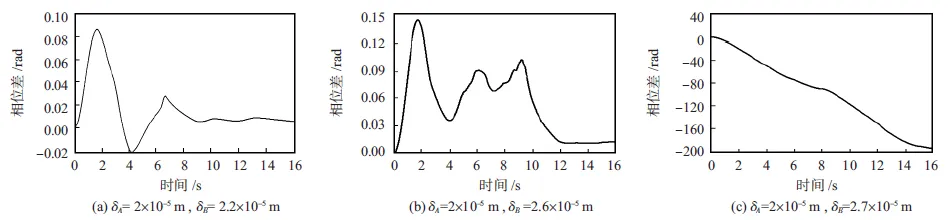
图3 不同柱塞副间隙下相位差

图3所示为两马达在不同柱塞副间隙值状态下，两偏心块的相位差动态变化曲线。

分析可知，当马达A柱塞副间隙2×10-5m、马达B柱塞副间隙在(2～2.6)×10-5m之间时，两偏心块的相位差经短时间过渡后，分别收敛为0.001 rad和0.022 rad；过渡时间分别为10.2 s和11.8 s，可以实现同步振动。当两马达柱塞副间隙值之差加大时，过渡时间延长，两偏心块相位差变化的峰值增大。图3(c)表示的是大柱塞副间隙时，两马达相位差变化曲线。当δA=2×10-5m，δB≥2.7×10-5m相位差快速发散，无法实现同步振动。

为将仿真结果的应用能进一步延伸，本文以《机械设计手册》中的多种规格柱塞马达的不同尺寸柱塞副为研究对象，进一步对双马达耦合同步能力进行仿真，得到了满足同步条件下的不同规格马达的柱塞副间隙差值取值范围[11,12]。其结果如表2所示。表中，x=(δBmax-δBmin)/δA。

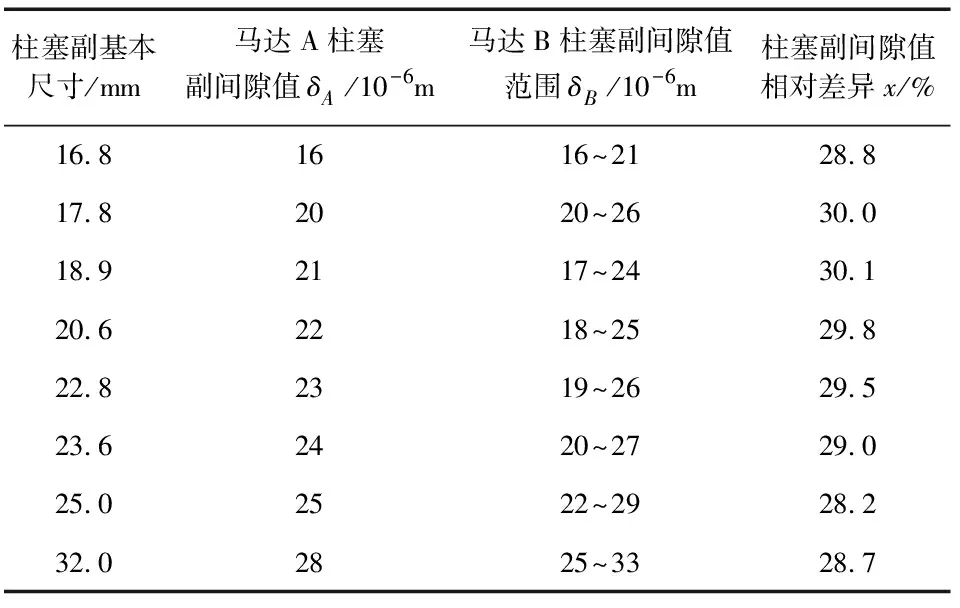
表2 满足同步条件下不同规格马达的柱塞副间隙值

分析表2可知，在满足上述耦合条件的基础上，虽然不同规格的马达对柱塞副间隙差值取值范围的具体数值有所区别，但双马达柱塞副间隙的相对差异基本一致，双马达耦合同步的条件为Δδ/δ≤25 % ，当满足该条件时双马达可实现无同步装置的协同作业。

5 结 论

基于双马达振动回转系统的物理耦合模型，研究了两马达内部结构差异引起的流量泄漏差异以及该差异对系统耦合同步能力的影响规律，得到了评价系统同步能力的耦合模型。通过MATLAB/Simulink数值模拟及现场试验，研究结果显示，当双马达柱塞副间隙的相对差异Δδ/δ≤25 %时，双马达可实现同步耦合。