Majorana零模式的电导与低压振荡散粒噪声∗

颜志猛 王静 郭健宏

(首都师范大学物理系,北京 100048)

1 引 言

在凝聚态系统中寻找并探测Majorana零能量模式(Majorana zero modes,MZM)引起了人们的极大兴趣[1,2].MZM是自身的反粒子,满足非阿贝尔交换统计性[3,4].通常的电子可以等价地看成一对MZM的线性组合,因此每对MZM可构成一个量子比特.而MZM作为“半个电子”,其交换会改变由成对MZM构成的量子态,可实现拓扑量子计算[5].作为非阿贝尔任意子,MZM的存在受拓扑保护,局域的环境干扰无法湮灭掉一个非局域的MZM,因此能有效地抵挡环境的退相干影响[6].

实现基于MZM的拓扑量子计算首先必须要有合适的材料体系,并测量体系是否具有非阿贝尔拓扑相,即需要确认MZM的存在.由InSb或InAs纳米线与s-波超导体构成的异质结构,结合超导电性、强自旋-轨道作用以及磁场能够实现拓扑超导态,产生MZM[7−9].该异质结构易于调制和操控MZM,被广泛用于目前的实验中[10−17].实验上,零偏压附近出现的反常电导峰被认为是MZM存在的可能证据[10−17].其他理论方案包括直接测量MZM的非阿贝尔统计性[18]、反常4π周期约瑟夫森效应[5]、自旋流关联函数[19]以及直接测量隧穿过MZM的电子噪声谱[20]等.但是,其他非拓扑的物理机制,比如,无序[21]、Kondo效应[22],特别是Andreev束缚态[23]都能产生类似的零偏压电导峰.并且,由于MZM是超导体的零能量模式,对电磁测量不敏感,以及超导体相位的脆弱性,使得实验上难以明确地证明MZM存在,还需要其他实验证据进一步甄别.

理论上提出将量子点(quantum dot,QD)与纳米线耦合,利用隧穿过QD的电子探测MZM[24−31].零温时,QD与MZM耦合使得零偏压处的电导峰减小1/2[24].大偏压极限下,电流与噪声能够证明QD-纳米线结构中存在MZM[25].Chen等[26]研究了类似模型在零温且有限偏压时的零频散粒噪声.大偏压极限下,零频全计数统计办法可探测相同结构中的MZM[27].Shang等[28]研究了MZM与双量子点耦合的Aharonov-Bohm干涉仪中的电导.Gong等[29−31]研究了量子点链式结构与MZM耦合的微分电导.诸多方案主要探讨了零偏压附近的反常电导峰[24,26,29−31],以及零温或大偏压极限的噪声谱[25,27].最近,实验上成功地将QD与InAs纳米线制备在一起,利用QD的微分电导谱观测到Andreev束缚态合并形成的MZM[15].

实验证据促使我们思考:既然MZM导致零偏压附近出现反常电导峰,那么(零)低偏压区的散粒噪声能否揭示MZM?为此本文考虑图1所示的QD-MZM耦合系统,采用主方程方法[32]研究了一般情况(有限温度与偏压以及有限频率)的散粒噪声.研究发现,MZM导致稳态电流差呈反对称,在零偏压处显示反常电导峰,表明存在MZM.但是,当QD与电极对称耦合时,电流差则无法区分MZM.而此时散粒噪声在低偏压区呈相干振荡,并在零频处显著增强.当QD与电极非对称耦合时,MZM使电子由反聚束到聚束输运,亚泊松噪声增强为超泊松噪声.稳态电流差结合低压振荡的散粒噪声能够证明MZM是否存在.

2 模型与理论方法

2.1 模 型

考虑QD与纳米线耦合的装置,如图1所示.当s-波超导体与具有强自旋-轨道作用的半导体纳米线接触,并施加较强的磁场,满足时,纳米线形成拓扑超导态,在其两端产生MZM,分别表示为γ1,γ2,满足Z是Zeeman劈裂能,与外磁场强度B成正比;µ与∆分别为纳米线的化学势和邻近效应引起纳米线中的超导带隙.QD与近邻γ1耦合,并处于强库仑阻塞区.整个系统的哈密顿量可写作:

这里Hl描述左、右两个金属电极,其中为电极电子的产生(湮灭)算符,电子波矢量与能量分别为k与εαk.Ht描述QD与电极间的隧穿耦合,耦合强度为tαk,设tαk∼tα与状态无关,假定电极的电子态密度ρα为常数,则电子隧穿率或能级线宽为Γα=2πρα|tα|2,单电子在QD与纳米线之间隧穿的时间约为1/Γα.Hs描述QD与MZM的耦合[24−27],其中d†(d)表示QD的电子产生(湮灭)算符;εD为有无电子占据的能量差,实验上可通过栅极电压调节该单电子能级;εM∼exp(−L/ξ)为MZM的分裂能,反映MZM波函数之间的重叠程度,L为纳米线的有效长度,ξ是超导相干长度;QD与近邻MZM的耦合强度为λ,一般地λ与QD-MZM的自旋有关.如果QD电子在磁场中的Zeeman劈裂能Es≫Γα且εD>0,则QD中自旋向下的电子能级(=εD+Es)将远大于费米能级,因此可以忽略自旋向下的电子输运.较大的Zeeman劈裂能同时也可抑制电子自旋的Kondo效应.本文考虑无自旋电子,λ取作实数.

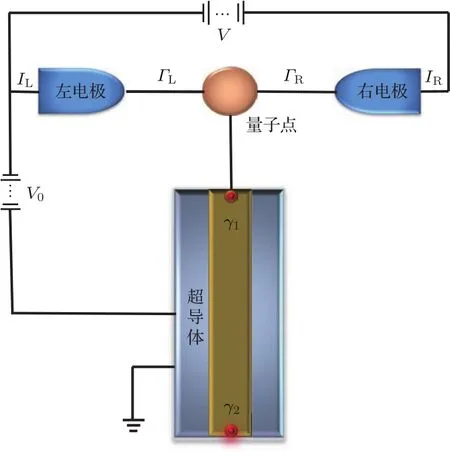
图1 QD与MZM耦合结构,其中QD与近邻MZM耦合,并与电极构成测量回路;取超导体化学势为能量参考零点,左右电极的化学势分别取作µL(R)=e(V0±V/2)(e为电荷电量)Fig.1.Schematic setup of a QD coupled to MZM.The QD is tunnel coupled to the nearest one of the MZM which are located at the two ends of the nanowire.The QD is connected to the electrodes,which forms a closed detection circuit.Choosing the chemical potential of the superconductor as the zero-energy reference,the chemical potentials of the left and right leads locate then atµL(R)=e(V0±V/2),respectively(with e the electron charge).

引入Dirac费米子f,表示纳米线中非局域电子的能级:满足反对易关系占据数为则哈密顿量Hs可写为

其中λ1=λ或λ1=0分别标记QD与MZM耦合,或QD与通常Dirac费米子的隧穿.λ1=λ时Hs表明非局域的nf态是电子与空穴的等权叠加态,nf=0→nf=1既表示电子从QD到纳米线的正常隧穿(∼df†),又描述纳米线释放一对电子分别占据QD与nf态而导致系统电子数不守恒的过程(∼f†d†).Hs在QD-MZM的直积表象|nD,nf⟩中分块对角化,nD与nf取0或1,分别表示QD或非局域费米能级上的电子占据,其中QD-MZM系统总电子数的宇称守恒,{|0,1⟩,|1,0⟩}构成奇宇称子空间,{|1,1⟩,|0,0⟩}构成偶宇称子空间,分别对应Hs分块对角化的部分.当εM=0时,奇、偶宇称子空间彼此等价;而εM=0会破坏这种宇称简并性.奇(偶)宇称子空间的本征态)为

本征能量Eo±(Ee±)分别为

2.2 理论方法

本文利用粒子数表象中的主方程描述体系的动力学[32].根据左电极发射出的电子数nL和右电极收集到的电子数nR,把系统状态划分成多重粒子数空间.将电极视为“环境”,中间QD-MZM系统用约化密度矩阵ρ(t)描述.设QD与电极耦合较弱,将ρ(t)的运动方程展开至Γα的二阶项,忽略系统能级的Lamb移位后,得到粒子数表象中的主方程:

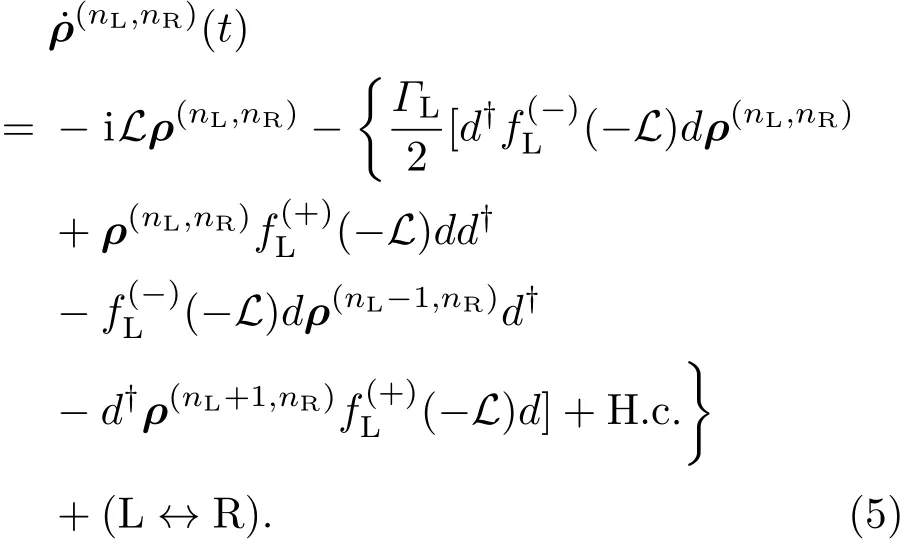
(5)式中(L↔R)表示将花括号中各项的L指标替换为R,即得到右电极对系统的耗散作用.刘维尔超算符L定义为描述系统的相干演化.费米函数描述电极的电子分布,其中µα为化学势;为Boltzmann常数,T为温度,并假定两个电极温度相同;f对电子数求和后可得并满足:

其中L0ρ描述在电极影响下QD-MZM系统的非幺正性演化,左右电极粒子数不变化;Jα±ρ分别表示电子从QD-MZM系统隧穿进α电极以及电子从α电极隧穿进QD-MZM的量子跳跃过程.

由于超导体使系统的电子数不守恒(∝df,d†f†), 故引入两个独立的计数变量χα(α=L,R),分别统计左、右电极隧穿电子数的变化,从而计算电极的电流.利用二维傅里叶变换

将方程(5)写作

(7)式中各超算符的具体形式在|nD,nf⟩表象中容易得到.利用(7)式可方便地计算稳态输运电流与散粒噪声.为此,引入累积生成函数G(χL,χR,t),

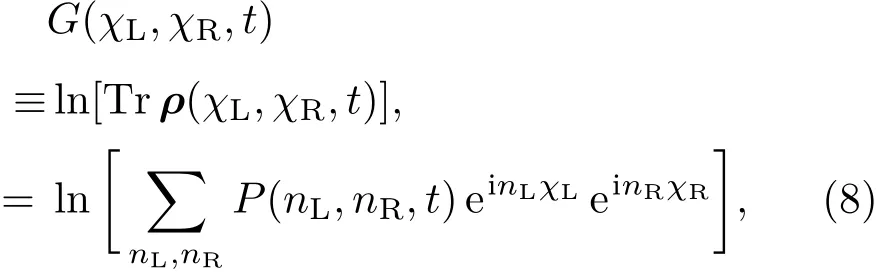
其中透射电子分布函数Tr表示对QD-MZM系统求平均.

利用G(χL,χR,t),求出各阶累积函数

其中,nα(t)为t时刻α电极发射或收集的电子数算符,可由(5)式对α电极的电子计数得到.在实际求解中,常利用拉普拉斯变换:

其中,1表示单位矩阵,ρst表示系统的稳态密度矩阵, 满足并设t=0时. 对(10)式分别计算相应计数变量χα的一阶与二阶偏微商,可得到稳态电流以及散粒噪声.

2.3 电流与散粒噪声

利用“跳跃算符”Jα±可得到流经相应电极的稳态电流为

QD-MZM系统的约化密度矩阵ρ(t)的演化方程可写成矢量方程,ρst表示列矢量|ϕ0⟩⟩,相应的左矢为行矢量满足因此元素1,0分别作用在ρst的对角元与非对角元上.超算符A的稳态平均值为则(11)式可简洁地表达为

其次,利用MacDonald噪声公式[33,34]:

以及二阶累积,可以证明(13)式中第二项⟨nα(t)⟩=Iαt, 恰好与第一项展开中的一部分相抵消.因此对第一项进行拉普拉斯变换后,即可得到散粒噪声

其中,符号表示对后面的代数多项式取实部.

3 模拟与讨论

利用(7),(12)以及(14)式可以方便地研究系统的电流与散粒噪声.以下分别研究电流与噪声随耦合强度Γα、分裂能εM以及温度T的变化情况.取~=kB=e=1,并以eΓL为能量基本单位.

3.1 电 流

由于左、右电极的电流不守恒,定义两极的电流差为

图2显示了在不同隧穿率Γα下电流差∆I随偏压V的变化.作为比较,图2给出了没有MZM的情况(λ1=0).没有MZM时,电子在QD与通常的费米子能级之间隧穿,系统的电子数守恒,∆I=0且不随Γα变化,在V=0处电子没有足够的能量隧穿进QD,电导为零.当纳米线进入拓扑超导区(λ1=λ),纳米线吸收来自QD和nf态的一对电子或者释放一对电子分别占据QD和nf态.当ΓL=ΓR时,∆I=0,说明QD与电极对称耦合时仅用电流或微分电导无法区分是否存在MZM.通过调节QD栅极电压,改变左、右隧穿结的透射率Γα,两极电流不再守恒,电流差相对于∆I=0呈非对称变化(图2(a)).

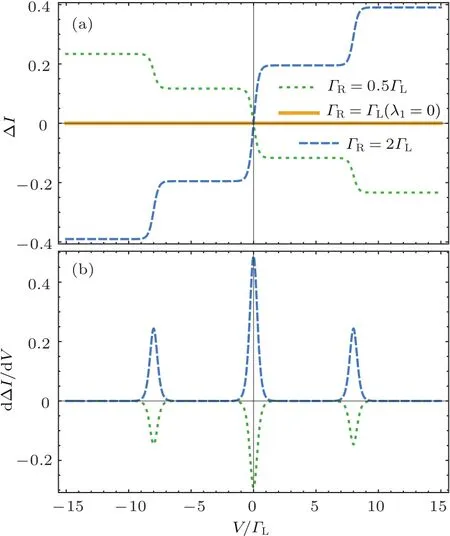
图2 不同隧穿率Γα下发射极与收集极电流差及其微分电导随偏压V的变化 (a)电流差;(b)相应的微分电导;其他参数"D=0;"M=0:1ΓL;λ1= λ =2ΓL;T=0:1ΓLFig.2.Differences between the steady-state currents and the differential conductances:(a)Current differences between the steady-state source and drain for different QD-MZM coupling values;(b)the differential conductances.Other parameters are"D=0;"M=0:1ΓL;λ1= λ =2ΓL;T=0:1ΓL.

在V=0处,只有MZM组成的零能量电子参与传导,因此出现零偏压电导峰.微分电导d∆I/dV可进一步说明电流差的台阶位置与非对称的物理原因(图2(b)),以正向偏压为例.电流台阶即电流产生跳变的位置由费米分布决定.当发射极的费米能级与系统不同宇称能级间的Rabi频率共振时,在处出现电导峰.QD与右电极耦合越强(ΓR≫ΓL),右电极越容易收集电子(包括超导体释放到QD上的电子),导致电流差增大且∆I>0,零偏压电导峰较高;反之,当ΓR≪ΓL时左电极发射的电子容易隧穿进QD与纳米线,在二者间相干振荡,由于时间尺度1/ΓR≫1/λ,电子不易隧穿进右电极,很容易被超导体吸收,而同时超导体释放到QD上的电子也难以被收集,使得右电极在∼1/ΓR内收集与左极在∼1/ΓL内发射出的电子数的绝对差值减小,电流差变小且∆I<0,零偏压电导峰降低.

下面重点研究非对称耦合ΓL=ΓR时的电流差.MZM之间的分裂能εM对电流有重要影响.实验上通过调节纳米线的栅极阵列,改变回路纳米线的有效长度,从而改变分裂能[10,14].理论[35]与实验[14]证明,εM随纳米线长度的增加呈指数衰减.对长度约1µm的纳米线,εM大约为0—50µeV.当Zeeman磁场介于拓扑平庸相与非平庸相的临界值附近时εM∼0[35].图3显示εM对电流差∆I的影响.随着εM增大,电流差逐渐减小,台阶向大电压区移动,即分裂能的增大抑制电流差.这是因为εM=0时,MZM波函数之间没有交叠,奇、偶宇称完全等价,当QD能级与εM共振时电子易于被超导体成对吸收和释放(∼2λ),右电极收集的电子数显著增多,电流差较大;通过调节纳米线的栅极阵列,改变纳米线的有效长度,使得MZM波函数的重叠增大.随着εM增大,奇、偶宇称的对称性受到破坏,QD与能级εM间的失谐量增大,引起奇偶宇称能量的分裂变大,电子不易被超导体成对吸收或发射,导致电流差减小,同时处的台阶向大偏压区移动.

图3 MZM分裂能"M对电流差的影响(其他参数"D=0,λ = λ1=2ΓL;ΓR=2ΓL;T=0:1ΓL)Fig.3. Current differences between the steady-state source and drain for different energy splitting"Mvalues.Other parameters are"D=0;λ = λ1=2ΓL,ΓR=2ΓL,T=0:1ΓL.

图4显示QD-MZM的耦合强度λ对电流差的影响.与εM类似,QD-MZM的耦合强度λ既影响电流差的大小,又改变台阶的位置.但是,与图3中εM显著不同的是,虽然电流差台阶随λ增大向大偏压区移动,但是电流差却随λ增大而增大.这是因为QD-MZM的耦合增强使得超导体更易于成对吸收或释放电子,在1/λ≪1/ΓR时间内右电极收集的电子数显著增加,两极间电流差增大.

图4 耦合强度λ对电流差的影响(其他参数"M=0:1ΓL;"D=0;ΓR=2ΓL;T=0:1ΓL)Fig.4.Current difference between the steady-state source and drain for different coupling λ values.Other parameters are"M=0:1ΓL;"D=0;ΓR=2ΓL;T=0:1ΓL.

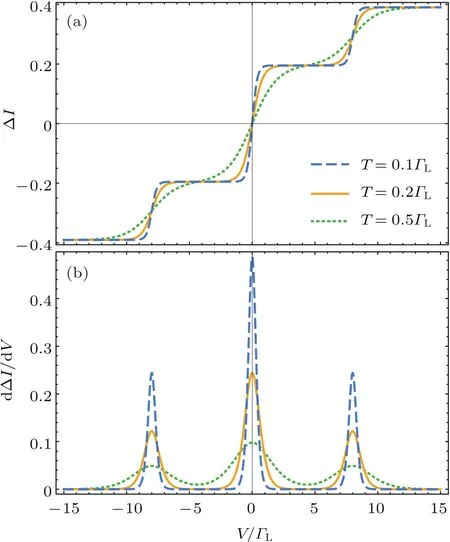
图5 温度对电流差及其微分电导的影响 (a)电流差;(b)相应的微分电导;其他参数"M=0:1ΓL,"D=0,λ1= λ =2ΓL,ΓR=2ΓLFig.5.Current differences between the steady-state source and drain and the differential conductances for different temperature T values.Other parameters are"M=0:1ΓL;"D=0;λ1= λ =2ΓL;ΓR=2ΓL.

图5给出了温度对电流差的影响.温度引起的热涨落反映在电极电子的费米分布中.温度较低时,∆I-V曲线存在明显的台阶且台阶陡峭.随着温度升高,费米面附近越来越多的电子参与输运,热涨落引起的电荷隧穿增强,导致电流差台阶逐渐变得平缓.但是,每个台阶的位置以及平台所代表的饱和电流差皆不变(图5(a)).V=0时,MZM导致的零偏压电导峰随温度升高而逐渐降低,并逐渐展宽(图5(b)).而没有MZM的库仑相互作用多能级系统中,V=0时电流(电导)为零[36,37].

3.2 散粒噪声

MZM耦合电子的散粒噪声不同于普通QD情形.散粒噪声能进一步表征MZM.下文重点研究对称耦合(ΓL=ΓR)的散粒噪声.

图6显示了有无MZM时的散粒噪声. 有MZM耦合时,噪声谱呈现“相干振荡”,表明在纳米线两端存在能量较低的MZM,与线内连续高能激发态之间存在能隙,因此纳米线两端的MZM与QD发生耦合,电子在QD与纳米线之间相干隧穿.说明MZM是分立局域的状态.其次,尽管噪声谱都呈振荡形式,但是MZM导致零频噪声显著增强(图6(b)),尤其是在低偏压区MZM使得零能量电子可以传导,因此低压散粒噪声依然呈相干振荡.相反,没有MZM时,V∼0附近的电子没有足够的能量而无法传导,致使低压噪声为零(图6(a)).比较低偏压(图6(c))与大偏压(图6(d))的噪声谱可见,低压振荡的散粒噪声是大偏压极限[25,27]无法揭示的.因此,零频噪声的显著增强以及低压相干振荡的散粒噪声能够证明存在MZM.

进一步,研究不同耦合时的噪声谱.首先,考虑MZM分裂能对噪声的影响,见图7.随着εM的增大,零频噪声减小并由峰逐渐变成谷.由(3)和(4)式知,当εD与超导体化学势共振时,奇偶宇称空间等价,相应能量的Rabi分裂相等.εM∼0时,电子在QD-纳米线之间相干振荡的频率约为2λ,SR(ω)在频率ω ≃±2λ处显现噪声谷.随着εM的增大,电子在QD-纳米线之间相干振荡频率变大,噪声谱振荡越发明显(图7(c)),谷的位置发生轻微移动(图7(d)).但是,εM的变化对大偏压区噪声台阶的位置与高度没有影响(图7(d)).

图6 散粒噪声 (a)没有MZM(λ1=0);(b)存在MZM(λ1=λ);(c)零电压V=0时有无MZM的噪声;(d)大偏压V=10ΓL 时有无MZM的噪声;其他参数"M=0:1ΓL;"D=0;λ1= λ =2ΓL;ΓL= ΓR;T=0:1ΓLFig.6.Shot noise:(a)Without MZM(λ1=0);(b)with MZM(λ1= λ);(c)V=0;(d)V=10ΓL.Other parameters are"M=0:1ΓL;"D=0;λ1= λ =2ΓL;ΓL= ΓR;T=0:1ΓL.

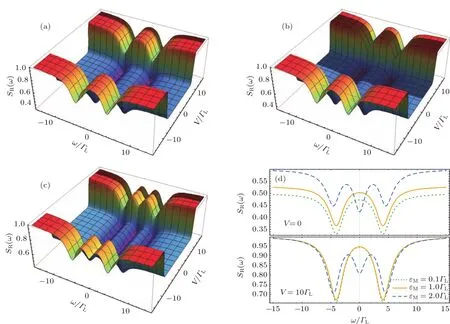
图7 分裂能"M对散粒噪声的影响 (a)"M=0:1ΓL;(b)"M=1:0ΓL;(c)"M=2:0ΓL;(d)V=0与V=10ΓL极限情况;其他参数"D=0;λ1= λ =2ΓL;ΓL= ΓR;T=0:1ΓLFig.7.Finite-frequency shot noise for different splitting energy"Mvalues:(a)"M=0:1ΓL;(b)"M=1:0ΓL;(c)"M=2:0ΓL;(d)V=0 and V=10ΓL.Other parameters are"D=0;λ1= λ =2ΓL;ΓL= ΓR;T=0:1ΓL.

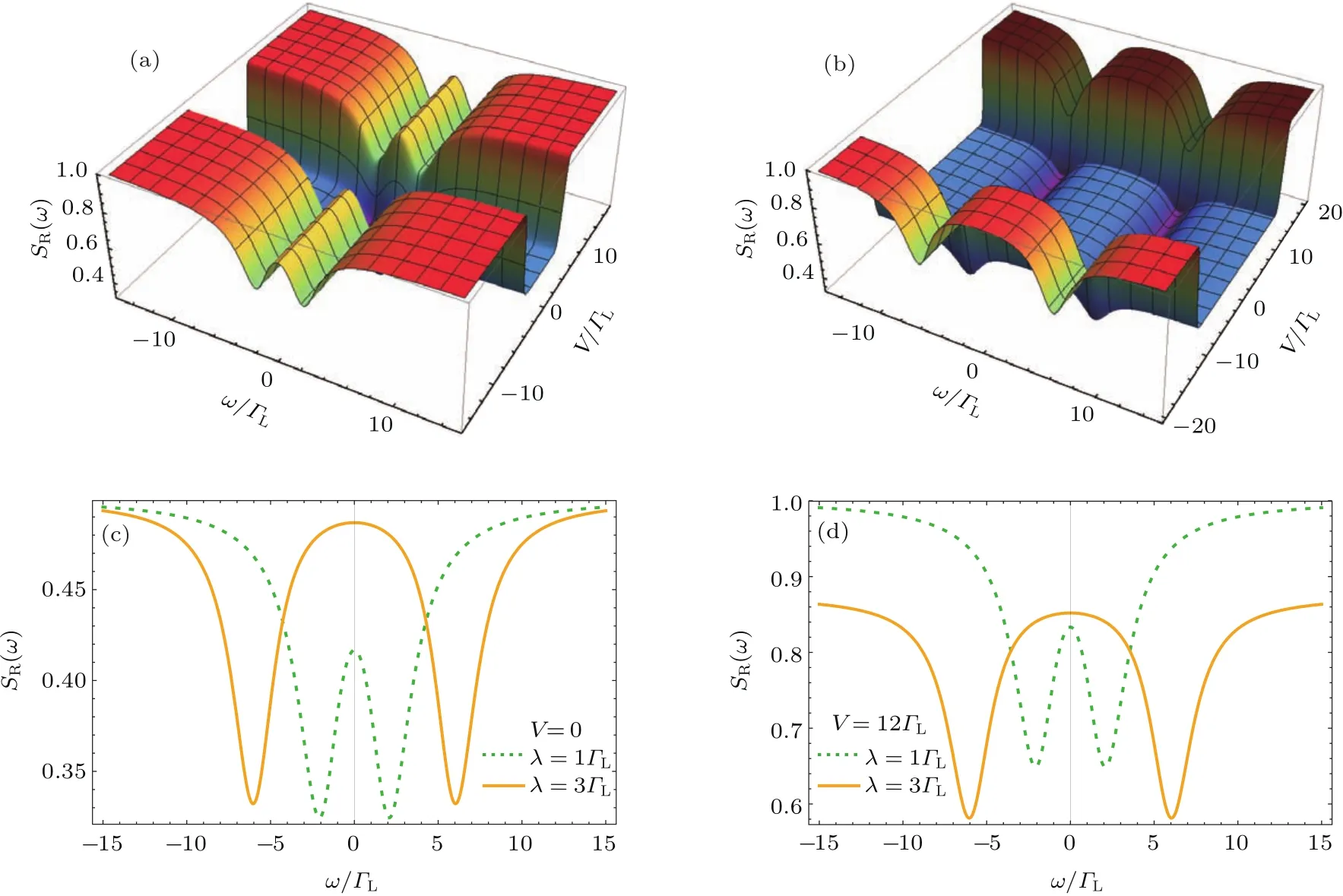
图8 耦合强度λ对散粒噪声的影响 (a)λ=ΓL;(b)λ=3ΓL;(c)V=0时λ的影响;(d)大偏压V=12ΓL时λ的影响;其他参数"D=0;"M=0:1ΓL;ΓL= ΓR;T=0:1ΓLFig.8.Finite-frequency shot noise for different coupling λ values:(a)λ = ΓL;(b)λ =3ΓL;(c)V=0;(d)V=12ΓL.Other parameters are"D=0;"M=0:1ΓL;ΓL= ΓR;T=0:1ΓL.

图9 系统与电极耦合强度Γα对散粒噪声的影响 (a)ΓR=0:5ΓL;(b)ΓR=ΓL;(c)ΓR=2:0ΓL;(d)ΓR=3:0ΓL;其他参数"D=0;"M=0:1ΓL;λ1= λ =2ΓL;T=0:1ΓLFig.9.Finite-frequency shot noise for different coupling Γα values:(a)ΓR=0:5ΓL;(b)ΓR= ΓL;(c)ΓR=2:0ΓL;(d) ΓR=3:0ΓL.Other parameters are"D=0;"M=0:1ΓL;λ1= λ =2ΓL;T=0:1ΓL.

图8显示QD-MZM耦合强度λ对噪声的影响.噪声谱依然呈相干振荡,由于εD=0且εM∼0,噪声谷出现在ω≃±2λ.但是与图7明显不同的是,由于λ增大,电子在QD-纳米线间相干振荡的频率加快,导致零频噪声增大,特别是低偏压V∼0附近SR(0)增大尤为显著(图8(c)和图8(d)).零频噪声峰展宽明显,噪声谷逐渐向高频端移动.而在偏压区,噪声台阶随λ增大而逐渐向大偏压区移动,直至大偏压极限下高频端SR(ω)→1.

实验上调节栅极电压可以改变Γα,从而改变电子在QD上的停留时间,因此QD与电极非对称耦合ΓL=ΓR也会影响电流及其噪声.图9显示,随着耦合强度ΓR的逐渐增大,噪声谱呈现显著的非对称相干振荡,零频噪声逐渐增强.当ΓL≫ΓR且ΓR<λ时,电子在QD与纳米线之间相干隧穿,容易被超导体成对吸收或释放,但右电极不易收集电子,导致收集极电流减小,噪声降低;而当ΓL≪ΓR且ΓR>λ时,电子能以较快时间隧穿进右电极,导致收集极电流增大,噪声增强.特别是,调节ΓR可使散粒噪声逐渐由亚泊松噪声(SR(ω)<1)变化为超泊松噪声(SR(ω)>1),说明在MZM耦合下电子由反聚束到聚束输运.而Γα的变化并不影响偏压区噪声台阶的位置.

4 结 论

本文利用主方程方法研究了QD-MZM混合结构中的稳态电流以及散粒噪声.MZM导致两极电流不守恒,电流差呈非对称性,并在零偏压附近有明显的反常电导峰,表明存在MZM.但是,QD与电极对称耦合时,电流差无法区分系统中是否存在MZM.而对称耦合时电子的散粒噪声谱在零偏压或低偏压区呈现“相干振荡”,且零频噪声显著增强.没有MZM的结构中低压散粒噪声则为零.进一步发现,当QD与电极非对称耦合时,MZM使电子由反聚束到聚束输运,亚泊松噪声增强为超泊松噪声.低压振荡的散粒噪声弥补了QD与电极对称耦合时电流差无法区分MZM的缺陷.因此,稳态电流差结合低压振荡的散粒噪声可以表征系统中是否存在MZM,有助于进一步利用输运方法明确观测固态结构中的MZM特征.