基于光子晶体光纤交叉敏感分离的磁场温度传感研究∗
吴倩 张诸宇 郭晓晨 施伟华
(南京邮电大学电子与光学工程学院,微电子学院,南京 210023)
1 引 言
磁场监测在许多领域,如海底环境监测、工业生产、军事工程、医学检测等,都有众多应用.但是在测量过程中环境温度的影响难以避免,因此,消除磁场温度的交叉敏感,并提高测量灵敏度是目前急需解决的问题.近年来,光子晶体光纤(photonic crystal fiber,PCF)传感结构因体积小、灵敏度高、结构灵活、设计多样、能够适应恶劣的检测环境和可实现远距离传感等优点成为国内外学者密切关注的课题[1−3].磁流体具有独特的磁光效应[4],其折射率随外加磁场变化而变化,既有固体磁性材料的可调节特性,又具有液体的流动性,易于填充,因此是一种良好的传感介质.
将PCF与磁流体相结合,可以间接测量出磁场参量.2014年,中国人民解放军理工大学的Li等[5]将磁流体注入双芯PCF的纤芯中,利用模式耦合实现了磁场传感.2017年,燕山大学的Liu等[6]在PCF纤芯中填充磁流体制成基于Sagnac干涉仪的磁场传感器.2018年东北大学的Li等[7]将马赫-曾德尔干涉效应与PCF结合完成磁场测量.同年,de Moutusi和Singh[8]选取了方晶格双芯PCF,通过在双芯中填充磁流体得到高精度的磁场传感器.然而,磁流体的温敏特性会影响磁场的检测,考虑到温度在实际应用中也是一个重要指标,所以实现磁场强度和温度的同时测量具有重要的实用价值.
本文提出了一种基于定向耦合效应和表面等离子共振(surface plasmon resonance,SPR)效应的PCF磁场温度双参量传感结构,分别产生定向耦合模式和SPR模式,当满足共振条件时[9,10],能量将发生转移,在光谱上表现为损耗峰,磁场强度和温度的变化会引起损耗峰的漂移.利用双通道结构同时测量磁场强度和温度并求解灵敏度系数矩阵[11],消除了温度和磁场强度的交叉敏感.
2 几何模型
基于定向耦合和SPR效应的PCF传感结构剖面如图1所示.考虑到结构参数对传感特性的影响,经优化后选定均匀包层空气孔间距Λ=11µm,空气孔直径d=0.4Λ,空气孔层数为4层.光纤基底材料为二氧化硅,其折射率可根据Sellmeier方程[12]算出.考虑到传感结构和传输光纤的模式匹配问题,并最大程度地降低光信号的损耗,本传感结构的外径设计为125µm.空气孔A中填充饱和磁化强度为0.85 emu/g(1 emu/g=10−3A·m2/g)的水基Fe2O3磁流体材料[13],形成磁场传感通道.空气孔B内侧镀有金纳米薄膜[14],厚度为40 nm,孔内填充温敏液体甲苯,作为温度传感通道.
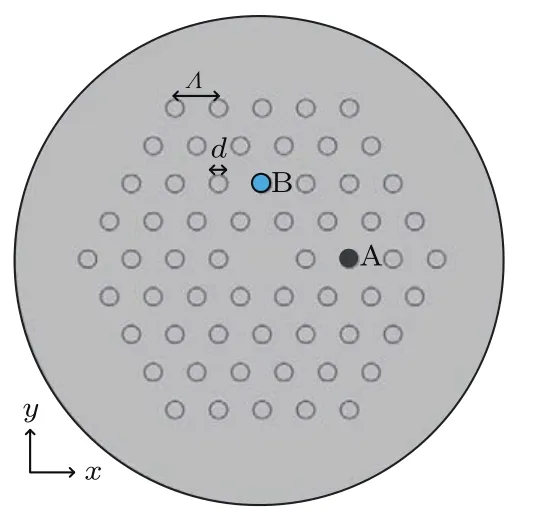
图1 基于PCF的传感结构剖面图Fig.1.Cross section of the PCF-based sensing structure.
2.1 磁流体折射率的数值分析
决定磁流体折射率的因素主要有:磁流体的粒子、基液、浓度、与温度密切相关的粒子的布朗运动、外加磁场和光俘获等[15].当磁流体的粒子和浓度确定时,可用郎之万函数[16]表示折射率nMF:

式中ns,n0分别为饱和状态和临界状态时对应磁场强度的折射率;Hcn为临界磁场强度;αMF为拟合参数;Ha和Ta分别为磁场强度(单位为Oe)和环境的热力学温度(单位为K).2003年Chen等[13]通过实验测试了磁流体的折射率,得出的数据与郎之万函数相符合.本文采用该磁流体实验数据进行仿真分析.由于磁流体折射率的饱和特性和临界特性,仿真时,选取磁场强度在90—270 Oe,温度在25—60◦C的范围内计算,此时磁流体有效折射率范围为1.4624—1.4670.
2.2 甲苯折射率的数值分析
甲苯的折射率[17]可以由Sellmeier方程和折射率温度线性关系得到:

式中λ为入射波长,t为环境温度(单位为◦C).甲苯的温敏系数αM为5.273×10−4/◦C,比基底二氧化硅的温敏系数[18]高两个数量级,因此可以不考虑基底折射率在测量过程中由温度引起的变化.
3 传感特性
利用COMSOL软件对基于PCF的磁场温度双参量传感结构进行数值分析,在各向异性的完美匹配层边界条件下[19],对模场的有效折射率在复数域进行求解.复数域的有效折射率,其实部是通常意义上的折射率概念,而虚部代表模式的损耗.
3.1 定向耦合传感特性
图2是在环境温度为25◦C,磁场强度为90 Oe时的定向耦合曲线.观察图2(a)中模式折射率实部与波长的曲线可以发现,随着波长增加,原始的两个模式将分裂成两个新的模式,且这两个模式在共振频率附近发生相互作用.在短波长处,纤芯模式HE11x模的能量被很好地限制在纤芯中,如图2(c-IV)所示.空气孔A中填充磁流体材料形成波导A,随着波长增加,能量逐渐转移到波导A模式TM1模中,最终在长波长处完全转移到TM1模中,如图2(c-VI)所示.波导A模式的能量转移规律与纤芯模式正好相反,在长波长处,波导A的能量最终完全转移到HE11x中,如图2(c-III)所示.
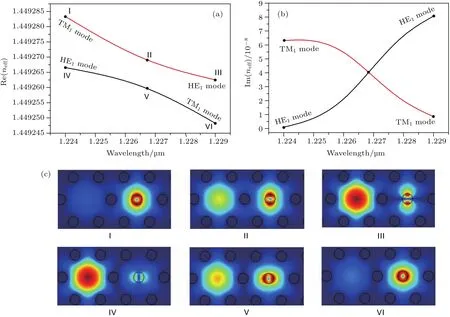
图2 (a)折射率实部与波长的曲线;(b)折射率虚部与波长的曲线;(c)纤芯导模与波导A耦合时的模场分布Fig.2.(a)Re(neff)and wavelength curves;(b)Im(neff)and wavelength curves;(c)mode field distributions for the coupling of core guide mode and waveguide mode A.
图2(b)所示的有效折射率虚部曲线直接从损耗的角度反映模式间能量的转移,可以看出,在短波处,随波长增加,纤芯模HE11x的损耗逐渐增大,能量逐渐由纤芯向波导A转移;在长波处,随波长增加,纤芯模HE11x的损耗逐渐减小,能量逐渐由波导A向纤芯转移.当波导A有效折射率和纤芯基模的有效折射率相等或相近时,发生共振耦合[20],对应波长即为共振波长λr,HE11x模在共振波长处出现明显的损耗峰.磁场强度的变化会引起λr的变化,因此,可以通过观察λr的移动来间接测量磁场强度.
3.2 SPR传感特性
空气孔B中填充温敏材料形成波导B,作为温度传感通道.接下来讨论温度传感通道的传感特性.图3是磁场强度为150 Oe,温度为25◦C时,纤芯导模的色散曲线、损耗曲线和等离子体模式的色散关系.其中黑色实线和红色实线分别代表纤芯导模和激发的等离子体模的有效折射率实部,蓝色虚线为纤芯导模虚部随波长的变化.由图3可知,在短波长处,纤芯和波导B的模式分别如图3内插图II,I所示,两者相对独立,没有发生相互作用.随着波长增加,当纤芯导模和波导B的有效折射率实部相等时,发生共振现象,如图3内插图III所示,此时纤芯的能量强烈地耦合至波导B中.蓝色虚线代表了纤芯模式的损耗,由于纤芯与波导B之间的能量转移,在纤芯的损耗谱上出现损耗峰.由于环境温度影响填充的甲苯液体折射率,从而导致损耗峰位置的改变.因此可以通过纤芯导模的损耗峰位置间接测量温度参量.

图3 纤芯导模与波导B耦合时的模场分布,其中黑色实线代表SPR模的折射率实部,红色实线代表纤芯模的折射率实部,蓝色虚线代表纤芯模损耗曲线Fig.3.Mode field distributions for the coupling of core guide mode and waveguide mode B.The black solid line represents the refractive index real part of the SPR mode,the red solid line represents the refractive index of the fiber core mode,and the blue dashed line represents the loss curve of the fiber core mode.
4 磁场和温度传感特性与交叉灵敏度求解
4.1 定向耦合效应下共振波长漂移
由于磁流体的磁光特性,其在定向耦合下的共振波长λr随磁场强度H变化,同时温度T也会引起λr的漂移.在温度固定时,通过仿真得到定向耦合效应下的波长-磁场强度漂移曲线,如图4(a)所示.由图4(a)可知,在温度不变的情况下,定向耦合效应下的共振波长与磁场强度的关系可用分段的线性拟合表示,即共振波长变化量∆λd,r1与磁场强度变化量∆H成正比,即

其中k1称为定向耦合效应下磁场强度引起的共振波长漂移灵敏度,在磁场强度为90—180 Oe时,k1=1.16 nm/Oe,在磁场强度为180—270 Oe时,k1=0.431 nm/Oe.

图4 定向耦合效应下,(a)共振波长随磁场强度的变化和(b)共振波长随温度的变化Fig.4.(a)Variation of resonance wavelength with magnetic field intensity and(b)variation of resonance wavelength with temperature under directional coupling effect.
同理可以得到固定磁场强度时,定向耦合效应下的波长-温度漂移曲线,如图4(b)所示.通过线性拟合,可以得到在磁场强度不变时,定向耦合效应下共振波长变化量∆λd,r2与温度变化量∆T满足

其中k2=−2.52 nm/◦C,称为定向耦合效应下温度引起的共振波长漂移灵敏度.由于磁流体的温敏系数为负,所以在定向耦合效应下随着温度的增加,共振波长发生蓝移,相应温度灵敏度为负.
定向耦合效应对应的共振波长受磁场强度和温度共同影响,因此环境温度T与磁场强度H对共振波长的影响可以叠加为
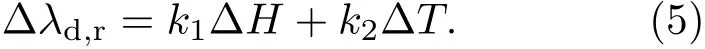
4.2 SPR效应下共振波长漂移
由于甲苯对磁场强度不敏感,所以SPR效应下磁场强度引起的共振波长漂移灵敏度可以认为是零.因此可通过分析SPR效应下的共振波长位置直接得到温度信息.
SPR效应下的波长随温度的变化如图5所示,满足线性关系.同上述分析可得:SPR效应下共振波长变化量∆λs,r3与温度变化量∆T满足
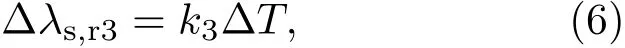
其中k3=−9.07 nm/◦C,称为SPR效应下温度引起的共振波长漂移灵敏度.

图5 SPR效应下共振波长随温度的变化Fig.5.Variation of resonance wavelength with magnetic field intensity under SPR effect.
4.3 磁场温度双参量解调
根据双参数解调原则,得到灵敏度系数矩阵:

对该矩阵求逆矩阵可得

将拟合得到的温度、磁场强度引起的共振波长漂移灵敏度数值代入矩阵中得到以下结果:当磁场强度较小,即在90—180 Oe时,

因此,当环境温度与磁场强度同时变化时,只需求得SPR效应与定向耦合效应下共振波长的变化量,即可通过(9)式得到环境温度与磁场强度的变化量,再由初始值最终得到磁场强度和温度.
5 结 论
基于定向耦合和SPR两种传感效应,提出了一种PCF磁场温度双参量传感结构,磁场强度和温度的传感灵敏度最高可达1.16 nm/Oe与−9.07 nm/◦C.在PCF的一个空气孔中填充磁流体形成定向耦合传感通道,在另一空气孔中镀上金纳米薄膜并填充温敏液体甲苯形成SPR传感通道.由于两种传感机理对外界环境的灵敏度不同,因此可以在出射光谱中找到两个共振峰,通过建立灵敏度系数矩阵可以分别求出磁场强度和温度的变化量.与现有的磁场传感器相比,本文提出的传感结构优势在于:不增加其他器件,PCF传感结构就可以完成磁场强度和温度的双参量测量,消除了磁场温度的交叉敏感.

