利用窄刻槽金属光栅实现石墨烯双通道吸收增强∗

高健 桑田李俊浪 王啦

1)(江南大学理学院光电信息科学与工程系,无锡 214122)

2)(江南大学,江苏省轻工光电工程技术研究中心,无锡 214122)

1 引 言

石墨烯作为一种由单层碳原子构成的二维材料,其独特的光电性质受到人们广泛关注[1].在可见光至近红外波段.由于石墨烯自身不能支持表面等离子体激元(surface plasmon polariton,SPP)的传输,单层石墨烯的光吸收由其精细结构常数α决定,对应频率无关的本征光吸收率仅为A=πα≈2.3%[2],极大地制约了石墨烯在光电探测等领域的应用.为此,人们提出将石墨烯与微纳结构相结合来增强石墨烯的光吸收率,涉及的增强吸收机理包括干涉效应[3]、介电常数近零效应[4]、导模共振[5−7]、法布里-珀罗(Fabry-Pérot,FP)共振[8,9],SPP共振[10,11]、磁偶极共振[12,13]、法诺(Fano)共振[14,15]等.

近年来,随着研究的深入,石墨烯增强吸收的功能开发与特性调控备受人们重视,包括宽带吸收特性[4,11,16,17]、可调谐吸收特性[5,13,18,19]、角度选择吸收特性[4,6,7,20]、角度不敏感吸收特性[4,17,21,22]、消偏振吸收特性[23,24]等.多通道吸收特性作为一种重要吸收特性尽管也被广泛研究,但均集中在红外至太赫兹波段[12,16,17,22,24−29].2017年,Liu等[30]利用二维银纳米盘微结构阵列在可见光波段实现石墨烯的双通道吸收增强,并指出双通道的吸收增强分别源于结构中SPP共振和磁偶极共振.然而,目前可见光波段有关石墨烯增强吸收的研究,涉及多个吸收通道及其增强吸收机理的研究还非常少.

本文提出利用窄刻槽金属光栅在可见光波段实现石墨烯双通道吸收增强的设计,在共振波长为462和768 nm处,单层石墨烯的光吸收率分别为35.6%和40.1%,相比石墨烯本征光吸收率的增强均高于15.5倍.研究发现,短波长和长波长的增强吸收分别源于金属光栅激发的SPP共振和窄光栅刻槽支持的FP共振,采用简化模型可估算出双吸收通道所在位置.此外,研究参数变化对吸收特性的影响发现,由于短波处吸收增强源于Au光栅激发的SPP共振,其吸收特性受覆盖层厚度、刻槽深度和宽度变化的影响较小;而长波处的吸收增强基于Au光栅刻槽中的FP共振,因而该吸收通道具有良好的角度不敏感特征.

2 结构设计与模型

图1为窄刻槽金属光栅实现石墨烯双通道吸收增强的结构示意图,刻槽深度和宽度分别为d和w的Au光栅位于SiO2基底之上,Au光栅被SiO2填充并在上方形成厚度为t的覆盖层,石墨烯位于SiO2覆盖层上方,横磁(transverse magnetic,TM)偏振光波(磁场沿y方向)以入射角θc从空气一侧入射,Au光栅的周期及膜层厚度分别为Λ和D.在设计中,为了保证石墨烯对入射光波的高吸收效率Au光栅采用亚波长结构.此时光栅周期满足Λ<λ/(1+sinθc);Au膜层厚度D=100 nm,大于其在可见光波段的趋肤深度.因此没有透射光,此时结构的光吸收效率可简化为A=1−R,其中R为结构的光谱反射率.

图1 窄刻槽金属光栅实现单层石墨烯双通道吸收增强示意图Fig.1.Schematic of metal grating with narrow grooves for dual-band absorption enhancement of monolayer graphene.

采用基于时域有限差分法的仿真软件FDTD Solutions,对窄刻槽金属光栅石墨烯增强吸收特性进行仿真计算. 在可见光波段,SiO2的介电常数εSiO2=2.16;石墨烯的介电常数为其中,t0=0.34 nm为单层石墨烯的厚度,ω为入射光的角频率,ε0为真空介电常数,σg为石墨烯电导率.σg是带内跃迁和带间跃迁的电导率之和,即σg=σintra+σinter,相应的表达式分别为[31]

式中,~为约化普朗克常数,T为开尔文温度,e为电子电荷量,kB为玻尔兹曼常数,Γ=1/(2τ)为载流子的散射率,τ=0.5 ps为动量弛豫时间,µc=0.15 eV为石墨烯的化学势[7].

Au材料介电常数可用Drude模型表达为

式中,ωp为等离子体频率,γ为阻尼系数. 对于本文研究波段,Au的ωp=1.32×1016rad/s,γ=1.2×1014rad/s[32].当TM偏振光从空气一侧入射至Au光栅并激发SPP共振,对应的波矢匹配条件满足:

式中,c为真空中光速;kSPP为SPP波矢,kSPP=m为光栅衍射级次. 对于由±1级衍射级次激发的SPP模式,正入射条件对应的SPP共振波长可简化为λSPP=

此外,石墨烯的光吸收可以从结构对应的全部光吸收中区分出来,相应单层石墨烯的光吸收率表述为[10]

式中,Pin是波长为λ的入射光功率,Pup(λ)和Pdown(λ)分别是经过石墨烯层上方和下方平面对应的光功率,上述功率参数可通过时域有限差分场分布计算获得.

3 仿真结果与分析

3.1 双通道光吸收机理分析

图2为窄刻槽金属光栅石墨烯结构的增强吸收光谱和峰值位置处的磁场分布,结构参数为:Λ=450 nm,D=100 nm,w=35 nm,d=70 nm,t=10 nm,TM偏振光波正入射.从图2(a)可以看到,结构在波长分别为λ1=462 nm和λ2=768 nm位置处产生双通道吸收增强,结构和石墨烯的光吸收率均达到最大值,其中石墨烯在短波和长波位置处的光吸收效率分别为35.6%和40.1%,相比石墨烯本征光吸收率的吸收增强均超过15.5倍.从图2(b)可以看到,短波位置处λ1的吸收峰光场能量主要集中在金属光栅表面,具有明显的SPP模式特征;采用本文简化模型估算的共振波长λSPP=476 nm,与短波长的吸收峰位置λ1=462 nm基本符合,这进一步证实短波处的增强吸收峰源于SPP共振.

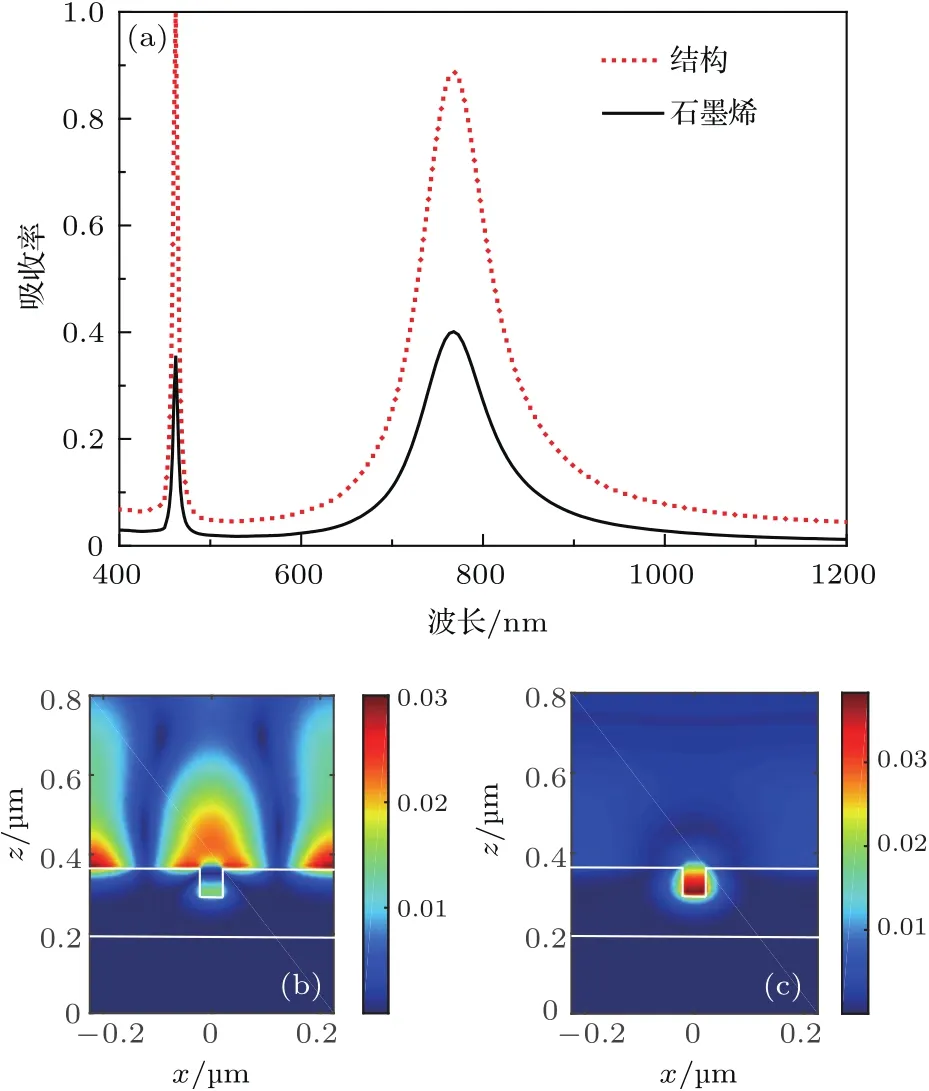
图2 (a)窄刻槽金属光栅石墨烯结构的全部吸收光谱和结构中石墨烯的吸收光谱;(b)峰值波长λ=462 nm处结构的磁场分布;(c)峰值波长λ=768 nm处结构的磁场分布Fig.2.(a)Absorption spectrum of total absorption of the structure containing substrate/narrow groove metal grating/covering layer/graphene,and absorption spectrum of graphene in the structure;(b)magnetic field distribution of the structure at peak wavelength of λ=462 nm;(c)magnetic field distribution of the structure at peak wavelength of λ=768 nm.

对于长波处λ2=768 nm的吸收峰,从图2(c)可以看到,结构中光场能量主要局域在金属刻槽中,具有显著的腔共振特征.由于SPP共振在金属刻槽中产生强烈的电磁耦合,光场能量被光栅刻槽所束缚,局域的光场能量逐渐泄漏并被刻槽上方石墨烯层吸收,引起单层石墨烯光吸收效率的显著增强.根据FP腔共振模型,此时共振位置取决于刻槽深度d和刻槽的有效折射率,可以表示为[33]

式中,N为正整数;neff为刻槽的有效折射率,可等效为金属-介质-金属(MIM)波导的模式折射率,其大小与SiO2和Au材料介电常数有关,也与Au刻槽宽度w有关,由于本文的光栅刻槽宽度极小,结构中仅支持TM0模式,对应的neff可通过MIM波导的偶模式色散关系确定[34],

其中,k0为入射光波矢,β为MIM波导模的传播常数,有效折射率neff=β/k0.在图2的结构参数下,估算得到的FP共振位置为658 nm,与实际吸收峰位置λ2=768 nm偏差较大.这是由于类FP腔的长度受到光栅上方SiO2覆盖层的影响,这层SiO2覆盖层的存在会使类FP腔的长度变长[35].假如计入t=10 nm这一SiO2覆盖层的厚度,估算得到的FP共振位置为743 nm,与实际吸收峰位置非常接近.此外,研究发现,进一步增加刻槽深度d的大小,SiO2覆盖层厚度对类FP腔长的影响所占比重将下降,直接采用刻槽深度d估算得到的FP共振位置与实际吸收峰位置的符合程度将随d的增大而不断提高;但d的增加会减弱刻槽中磁场增强效应,导致结构和石墨烯的光吸收效率均下降

3.2 参数变化对吸收特性影响分析

图3为不同刻槽宽度w对应的石墨烯吸收光谱,其他结构参数与图2相同.从图3可以看到,当刻槽深度w在15—55 nm范围内变化时,短波长的吸收特性对刻槽宽度的变化不敏感,w偏离设计值使得短波长的光吸收效率略有降低,但吸收峰位置几乎不变;由(4)式可知波矢匹配条件与刻槽宽度无关,SPP共振波长位置几乎不受刻槽宽度影响,因而短波长的吸收特性受刻槽宽度变化的影响甚小.而对于长波处的吸收峰,刻槽宽度的变化不仅改变吸收效率和吸收带宽大小,吸收峰位置也变化显著;由(6)式计算发现,增加刻槽宽度将减小MIM模式的有效折射率neff,因而吸收峰位置将随w增加发生蓝移.

图4为不同刻槽深度d对应的石墨烯吸收光谱,d由60 nm增加到80 nm,其他参数与图2相同.从图4可见,当光栅深度d变化时,情况与图3类似,由于短波长对应的光吸收增强源于SPP共振,光场能量主要局域在Au光栅表面,因而d的变化对石墨烯的吸收特性几乎没有影响.与之不同的是,由于长波处的吸收增强效应源于FP共振,因此吸收峰的峰值吸收率、吸收带宽和峰值位置受d的变化影响较显著;由(5)式可知,由于增加d将增大FP腔的腔长,FP谐振腔的腔长越长,谐振频率越低,因此长波处吸收峰位置随d的增加而红移.可见,由于FP共振与刻槽宽度w和深度d密切相关,通过选择不同的w和d,可以调控石墨烯在长波处吸收峰的峰值位置,这在实际应用中具有一定价值.

图3 刻槽宽度w变化对石墨烯吸收特性的影响Fig.3.In fluence of slit width w on the absorptionproperties of graphene.

图4 刻槽深度d变化对石墨烯吸收特性的影响Fig.4.In fluence of slit depth d on the absorption properties of graphene.

图5为不同SiO2覆盖层厚度t对应的石墨烯吸收光谱,其他参数与图2相同从图5可见,当覆盖层厚度t由10 nm增加到20 nm时,两个吸收通道的光吸收率均有所下降,且长波处的吸收峰位置向长波方向发生较明显的移动.分析对应的磁场分布发现,随着覆盖层厚度t的增加,处在Au光栅上方的石墨烯层逐渐远离增强的光场,SiO2覆盖层作为缓冲层在一定程度上减弱了光栅与石墨烯的电磁耦合,导致石墨烯双吸收通道光吸收效率的降低.此外,由于t的增加在一定范围内增大了类FP腔的长度,因此长波处的吸收峰位置随t的增加红移.

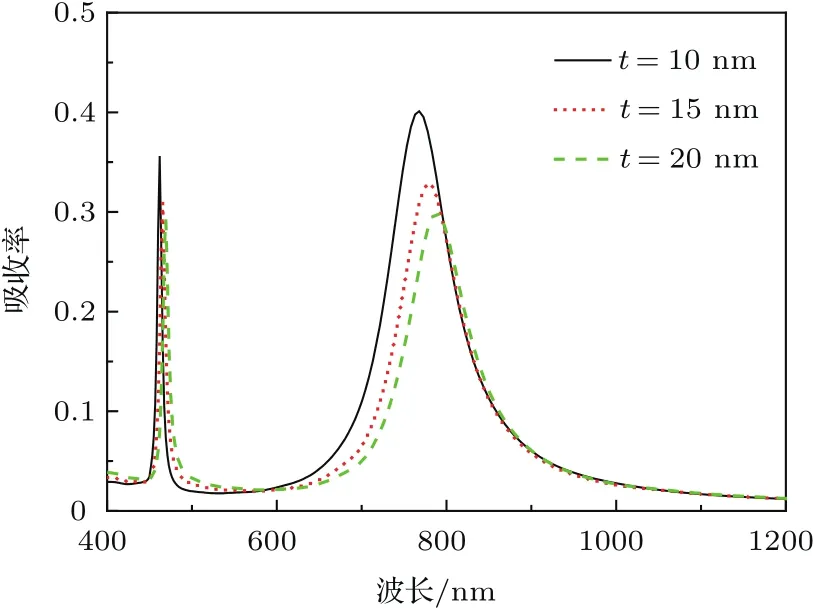
图5 覆盖层厚度t变化对石墨烯吸收特性的影响Fig.5.In fluence of thin- film thickness t on the absorption properties of graphene.

图6为不同入射角θc对应的石墨烯吸收光谱,光栅参数与图2相同.从图6可见,对于长波处吸收峰,由于其磁场能量较多地局域在Au光栅刻槽中,θc的变化几乎不影响刻槽的FP共振条件,因此吸收峰具有良好的角度不敏感特性;对于短波处吸收峰,由(4)式可知,入射角度变化将影响SPP共振的相位匹配条件,当入射光由正入射转变为斜入射时,±1级衰减衍射级次激发的SPP共振的简并性被破坏,导致+1级和−1级衍射级次对应的吸收峰分别向长波和短波方向移动,这一特性与导模共振光栅斜入射条件下反射峰劈裂现象类似[36].此外,随着θc增大,劈裂的−1级吸收峰将移至非亚波长波段,光场能量被传播的高级次衍射分配,因此对应−1级吸收峰的峰值光吸收效率较+1级低.

图6 入射角θc变化对石墨烯吸收特性的影响Fig.6.In fluence of incidence angle θcon the absorption properties of graphene.

4 结 论

采用窄刻槽Au光栅在可见光波段实现石墨烯双通道吸收增强,在462和768 nm波长处,单层石墨烯的光吸收率分别为35.6%和40.1%,相比其本征光吸收率的增强均高于15.5倍.研究发现短波处的吸收增强源于Au光栅激发的SPP共振,长波处的吸收增强源于Au光栅刻槽中的FP共振,采用简化模型可以估算出双吸收通道所在位置.此外,研究了参数变化对双通道吸收特性的影响,结果表明,由于覆盖层厚度、刻槽的深度和宽度与SPP共振的相位匹配条件无关,因此短波处的吸收特性几乎不受上述参数变化影响,但受入射角变化影响显著,偏离正入射将发生吸收峰劈裂现象;由于长波处吸收增强源于窄刻槽中的FP共振,因此它呈现出良好的角度不敏感吸收特性.基于窄刻槽Au光栅实现石墨烯双通道吸收增强在光电探测、太阳能电池等领域具有一定应用价值.