一种高光谱相机绝对辐射定标方法

刘贺雄,周 冰,高宇辰,贺 宣,鲁 军

(陆军工程大学石家庄校区电子与光学工程系,河北 石家庄 050003)

1 引 言

自高光谱技术诞生以来,各国都对其进行了深入的研究。目前,高光谱遥感技术已广泛应用于农业调查、矿物质勘探、环境监测等领域[1-2]。高光谱相机最显著的特点是可以将光谱技术和成像技术结合起来,获得特定目标区域特定波段的光谱图像数据[3]。高光谱相机在采集目标光谱信息之后的输出为DN(digital number)值[4]。DN值为量纲一数据,无法反应真实的目标辐亮度[5]。因此,在实际应用时需对高光谱相机进行辐射定标,确定探测器输出的DN值与辐亮度的关系,便于对被观测目标的光谱信息进行定量分析[6-7]。辐射定标可分为相对辐射定标和绝对辐射定标[8]。相对辐射定标指确定光谱相机各波谱段、各像源测得辐射量的相对值；绝对辐射定标指建立传感器入瞳处表观辐亮度与探测器输出的DN之间的关系[9-10]。

随着技术发展,高光谱技术被引入激光制导、激光测距等领域用于对特定区域特定波段背景辐射的测量。在激光制导、激光测距等领域的背景辐射研究中,所针对波段往往只有几个纳米,并要求得到实际的精确背景辐射量。因此不同于传统的高光谱遥感,对背景辐射测量要求对高光谱相机进行高精度、高分辨率的辐射定标,以得到某一区域特点波段精确的背景辐射绝对量。本文通过测量滤波片透过率得到各波段透过的能量占总透过能量的百分比,从而得到各波段的辐亮度,再建立其与相机探测器输出的各波段DN值的关系,实现绝对辐射定标的目的。

2 原 理

绝对辐射定标的基本内容是确定探测器入瞳处表观辐亮度与探测器数字化输出之间的关系[11]。假设高光谱探测器入瞳处的辐亮度为L(λ),则探测器某一像源接受到的辐亮度可表示为:

(1)

其中,F为系统的F数；τ(λi)为高光谱相机分光效率与光学系统透过率之积；θ为像源与光轴的夹角。

该探测器像源输出的DN值可表示为:

(2)

其中,λi为标定波段中心波长；δ(λi)为光谱分辨率；η(λi)为探测器量子效率；d为像源尺寸；Re为探测器电子增益；t为曝光时间；t为探测器暗电流；h为普朗克常量；c为光速。当δ(λ)很小时,根据式(1)、(2),DN可表示为:

(3)

进一步化简得:

DN(λ)=G(λ)L(λ)+B

(4)

其中:

B=ReIdt

由式(4)可知探测器入瞳处辐亮度与其输出DN值成线性关系。如果已知两组DN(λ)、L(λ)即可求得倍增系数G(λ)与偏置常数B,完成对某一波长的绝对辐射定标。

3 传统方法

目前实验室绝对辐射定标大多采用积分球输出的光做参考光源,通过调节积分球输出辐亮度的强弱对高光谱相机进行定标[7]。如图1所示,使用某波段的单色光作为积分球光源,再用高光谱相机采集其不同输出下的光谱图像,与此同时用辐射计测量输出能量计算辐亮度。在采集多组数据之后即可用最小二乘法确定入瞳处辐亮度与高光谱相机的数字化输出DN值之间的关系。

图1 传统高光谱定标方法图示Fig.1 Traditional hyperspectral calibration method

此方法定标的分辨率受限于积分球输出光的光谱宽度,只能标定某一较宽的波段,无法满足对光谱分辨率较高的高光谱相机进行定标的要求。

4 方法改进与数据处理

以白炽灯为积分球光源,使用德国inno-spec公司生产的The Redeye高光谱相机对其1056～1076 nm波段的输出光进行数据采集,采集步长1 nm,如图2所示,得到其波长与DN值的关系DN(λ)。利用美国瓦里安公司生产的分光光度计Cary 2000测定某滤波片的透过率τ1(λ),测量精度0.02 nm。利用τ1(λ)求得以λα为中心,步长1 nm的波段的平均透过率:

(5)

滤光片在1057～1075 nm波段,步长为1 nm时的平均透过率如图3所示,由图3可知,滤波片透过率从1057 nm至1075 nm先变大后边小,峰值出现在1066 nm处,峰值透过率约为87%。

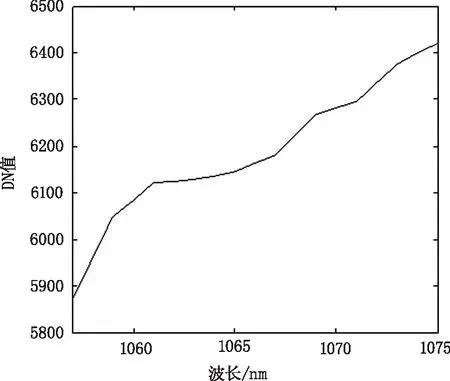
图2 积分球输出的DN值Fig.2 The DN value of the integrating sphere output

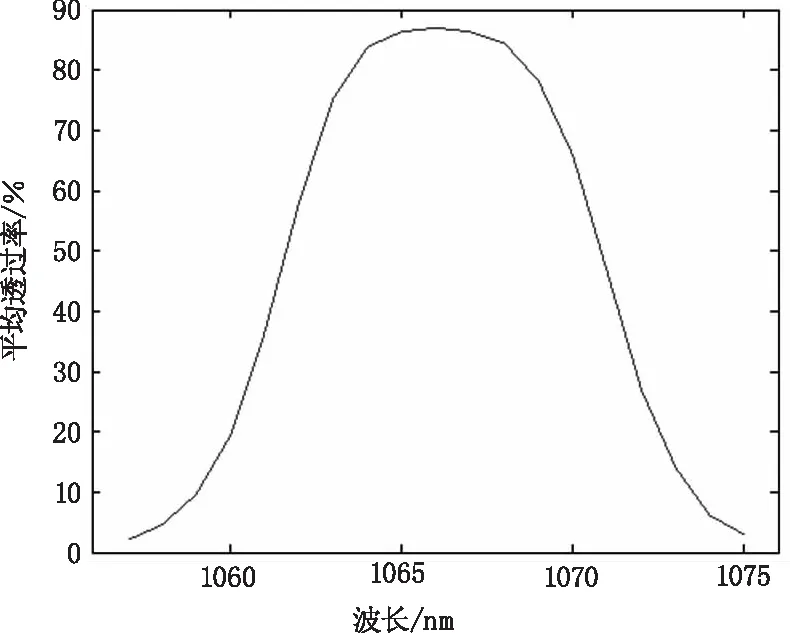
图3 滤波片步长为1 nm的平均透过率Fig.3 Average transmittance of the filter at 1 nm step size

根据DN(λ)、τ(λ)即可求取某一波段透过能量占透过滤波片总能量的百分比:

(6)

图4所示为各波段透过能量占透过滤波片总能量的百分比。各波段透过能量占透过滤波片总能量的百分比是由滤波片各波段平均透过率、积分球输出的各波段DN值共同决定的,由图可知1067 nm波段输出能量占比最大,约占总能量的10%。

将滤波片置于积分球输出孔前,用高光谱相机采集经过滤波片的输出光光谱信息,如图5所示,即为其波长与DN值的关系DNt(λ)。再用辐射计求出其辐亮度L,则以λα为中心,步长1 nm的波段透过滤波片的辐亮度为:

L(λa)=L·φ(λa)

(7)

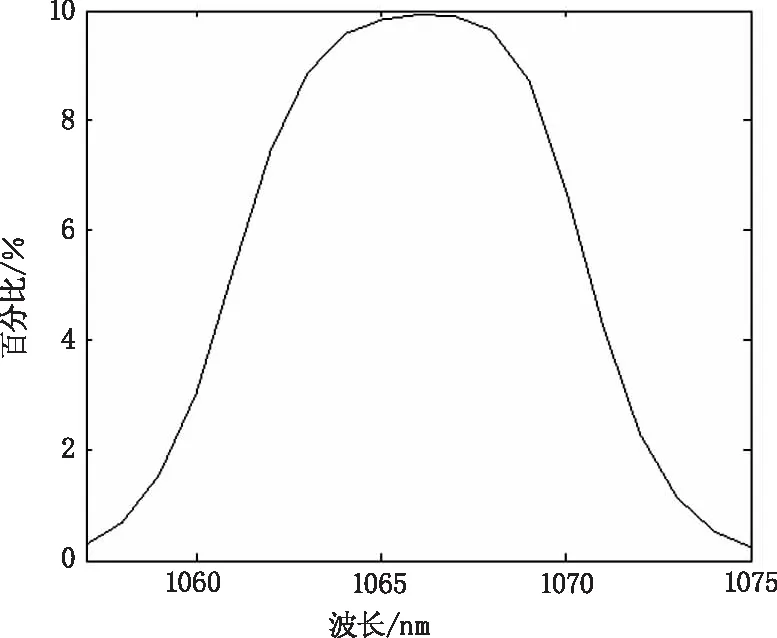
图4 各波段透过能量占透过滤波片总能量的百分比Fig.4 Percentage of transmission energy of each band in the total energy of transmission filter

图5 经过滤波片的输出光的光谱DN值Fig.5 Spectral DN value of the output light that passes through the filter

改变积分球输出光亮度,依照上述方法测得多组DN′(λ)、L(λα),通过最小二乘法即可求取其增益系数G(λ)、偏置量B,完成高光谱相机的绝对辐射定标。本文使用的高光谱相机在每次使用前都会进行去除暗噪声的操作,所以定标的偏置量B近似为零。所得增益系数如图6所示。

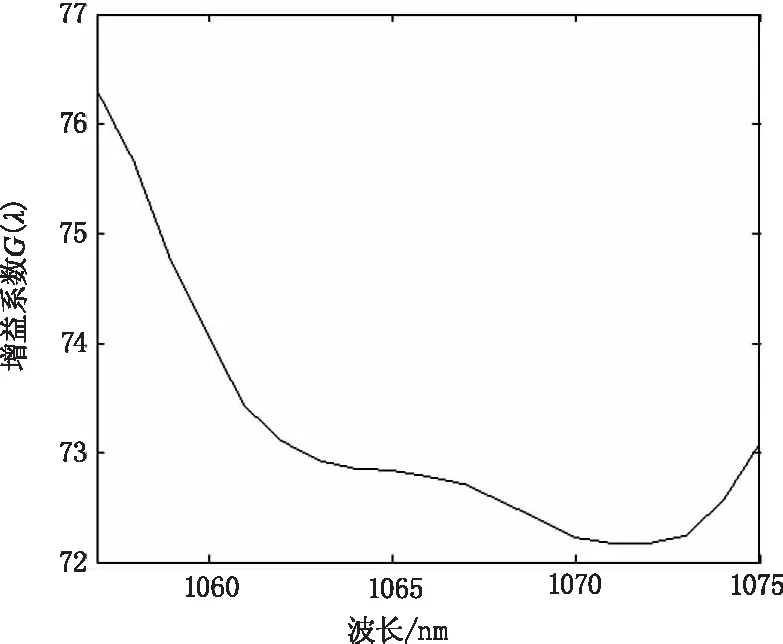
图6 不同波长下的增益系数Fig.6 Gain coefficients at different wavelengths

5 结 论

通过测量滤波片透过率与积分球输出的DN值得到各波段透过滤波片的能量占总透过能量的百分比,结合实际测得积分球出射并透过滤波片的辐亮度,得到各波段实际出射辐亮度,由此建立了各波段的辐亮度与相机探测器输出的各波段DN值的关系,完成绝对辐射定标。将提高高光谱相机定标分辨率,转变为提高测量滤光片透过率分辨率,简化了研究过程,达到了绝对辐射定标的目的。通过实验结果可以看出:高光谱相机对不同波长的光响应不一致。对于波长在较小范围内变化的光,高光谱相机对其的增益系数也会发生改变。