反焊盘设计及其对差分过孔高频特性影响分析
罗会容,何文浩
(1.江汉大学 物理与信息工程学院,湖北 武汉 430056;2.武汉中原电子集团有限公司,湖北 武汉 430074)
0 引言
在高速数字电路设计中,高速信号多采用差分信号传输方式。随着数字信号速率的不断提高,信号的上升沿越来越短,过孔产生的寄生效应易导致信号的阻抗不连续、反射、衰减等问题[1-4],影响过孔高频特性的因素成为大家关注的焦点。目前,对于过孔高频特性分析和研究集中在阻抗和结构优化、延时、内电层谐振、焊盘残装、非功能焊盘等方面[5-8],对影响差分过孔的反焊盘设计关注较少。本文通过等效过孔模型及理论计算对反焊盘进行预估计算,并根据计算值采用三维建模和仿真的方法对不同参数、形状反焊盘的差分过孔高频特性进行了分析,为高速差分过孔反焊盘设计提供了参考。
1 差分过孔模型与反焊盘参数
1.1 差分过孔简化模型
差分过孔模型可以简化成简单耦合传输线进行建模的方法分析差分过孔结构[9-10],如图1(a)所示。该等效模型的建立基于双杆、杆面和同轴电缆理想模型理论,如图1(b)所示。其中,L为双杆模型和同轴电缆模型纵向长度,s为双杆模型的圆杆间距,r为双杆模型的圆杆半径。假设理想模型介质材料均匀,且完全填充介质区域,其介电常数为DK,D1和D2分别为同轴电缆模型的内圆直径和外圆直径。
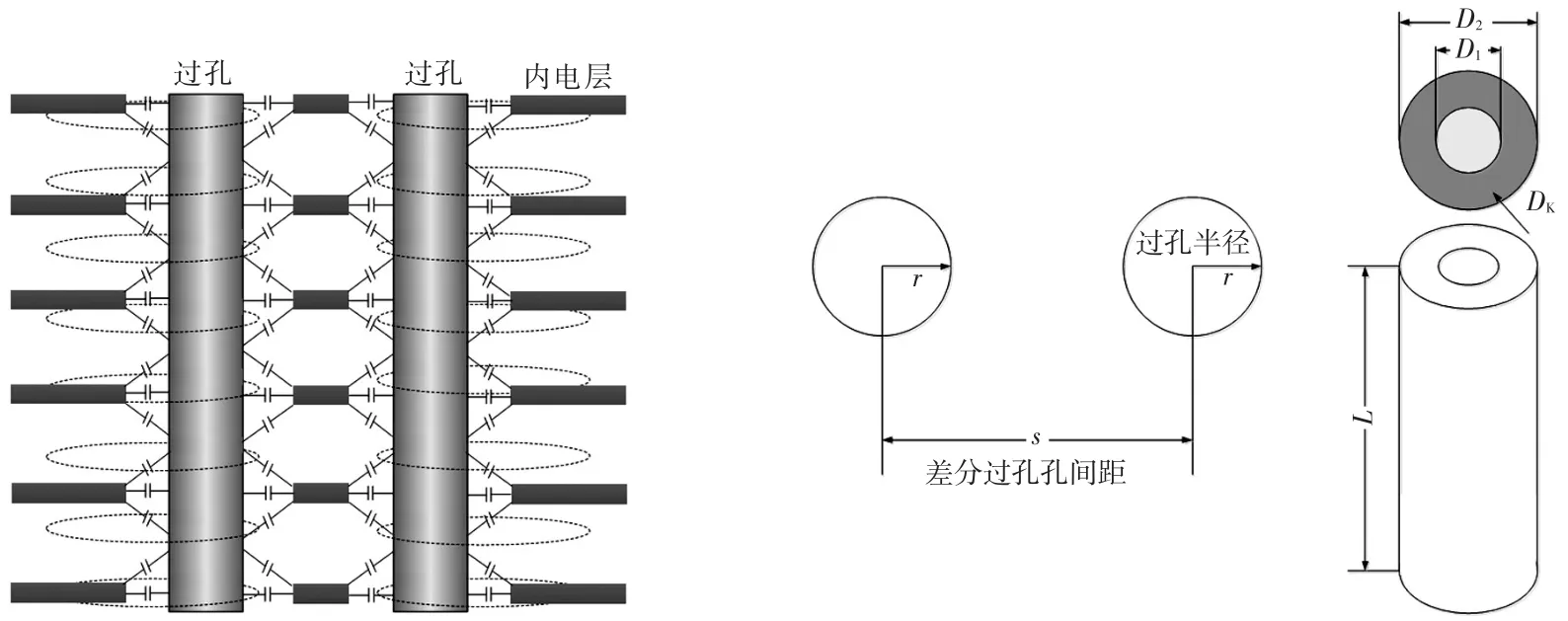
图1 过孔简化模型Fig.1 Simplified model of vias
1.2 差分过孔反焊盘参数分析
双杆模型的回路电感
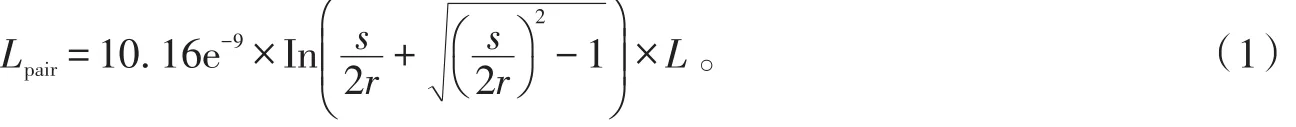
同轴电缆模型相当于将圆柱导体嵌入均匀介质材料中,最外层为理想连续金属平面,其分布电容

当差分信号加在双杆模型上时,双杆差分处于奇模状态,此时每根杆的特性阻抗称为奇模阻抗。双杆模型的奇模电感Ls等于双杆模型回路电感的一半,有

由此引出差分过孔等效模型,其奇模电容Cvs等于同轴电缆的分布电容Cco,奇模电感Lvs等于双杆模型的奇模电感Ls,其奇模阻抗Zvs计算如下:
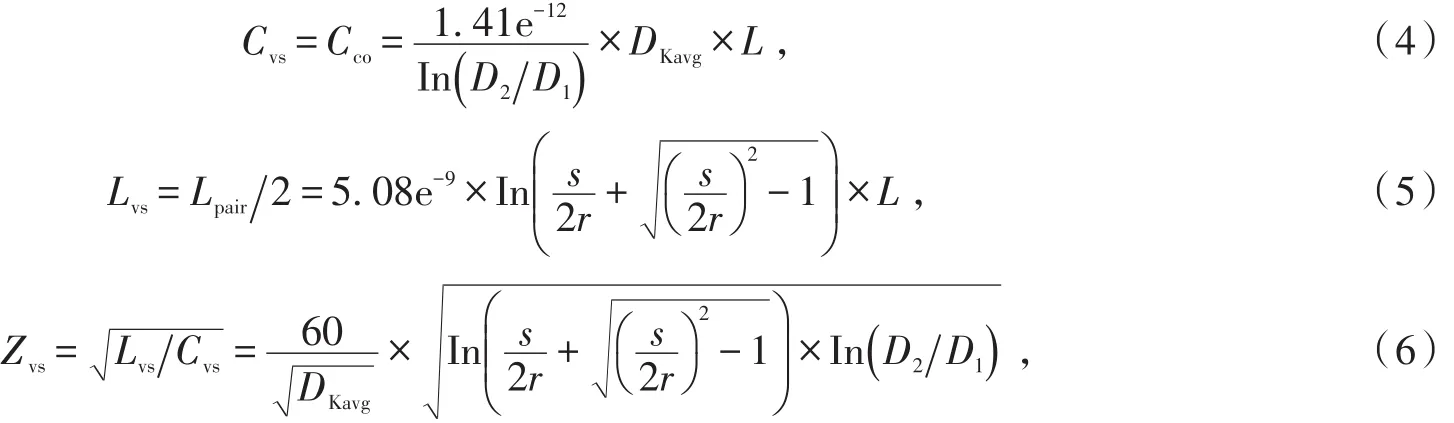
式中DKavg为平均介电常数,DKavg=(DKxy+DKz)∕2。其中,DKxy为平行于参考平面传输的x和y轴介电常数,DKz为平行于介质厚度传输的z轴介电常数。
由于差分阻抗是每根信号线与公共返回路径间阻抗的串联,则理想差分过孔模型差分阻抗
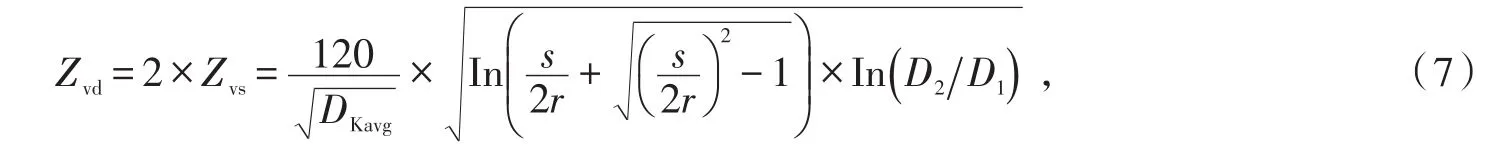
可以得到过孔反焊盘半径
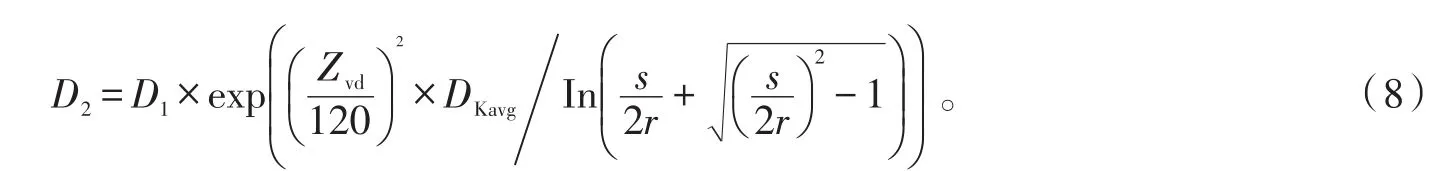
可用公式(8)进行过孔反焊盘参数计算,在一定阻抗设计目标下提供反焊盘参数范围,为HFSS仿真提供预估参数。
2 差分过孔反焊盘设计及仿真分析
采用HFSS仿真软件对印制板及差分过孔建模,测试PCB板共16层,第2、4、6、8、11、13、15层为地层,其他层为信号或电源层,差分线分布在顶层和第5层,板厚64.7 mil。
2.1 差分过孔建模
2.1.1 差分过孔模型 差分过孔孔中心间距40 mil,过孔直径12 mil,孔长Len=64.7 mil。N4000-13SI_PRE_1080板材介电常数DK=3.3,取DKavg=DK=3.3,HFSS差分过孔三维全波模型如图2所示。其中过孔出线长度为90 mil,初始反焊盘设计为单端圆形反焊盘,将所有参考平面进行挖空处理。
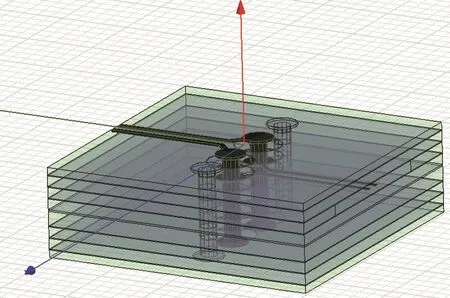
图2 HFSS过孔三维模型图Fig.2 3D model diagram of HFSS vias
2.1.2 反焊盘预估值计算 将差分阻抗设计目标值设定为Zvd=100 Ω,通过(8)式计算出单端反焊盘预估直径为
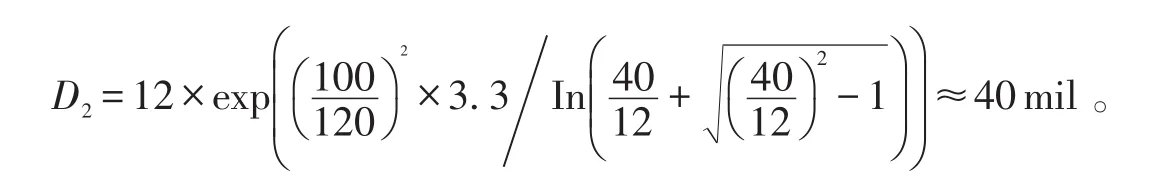
根据差分线阻抗一般误差允许范围±10%,在差分过孔阻抗分别为90 Ω和110 Ω时计算出反焊盘直径为Dmin=32 mil,Dmax=52 mil。
2.2 反焊盘参数带入仿真及分析
2.2.1 参数带入仿真 当反焊盘为圆形时,根据计算所得差分过孔反焊盘直径范围值32 mil≤D≤52 mil带入差分过孔HFSS模型进行仿真,选取TDR曲线、回损曲线、插损曲线3种高频特性曲线进行效果比较分析。当反焊盘直径分别为32、40、52 mil时,仿真结果如图3所示。
由图3(a)和图3(b)可知,在该差分过孔模型下,当频率小于22.2 GHz、差分过孔反焊盘直径为32、40、52 mil时自损S11和插损S21依次略好;当频率大于22.2 GHz时,自损S11和插损S21值并未随着反焊盘直径的增加而变好。由图3(b)可知,在该模型下过孔高频谐振频率随着反焊盘直径的增加而变高,反焊盘直径为32、40、52 mil时,其高频谐振频率依次为22.6、23.6、25.6 GHz。由图3(c)可知,反焊盘直径为32、40、52 mil时,差分过孔阻抗变化区间依次为[56.55 Ω,100.82 Ω]、[63.90 Ω,107.76 Ω]、[70.25 Ω,100.80 Ω],相对于差分过孔100 Ω参考阻抗值,变化幅度最大百分比分别为43.45%、36.10%、29.75%,即反焊盘直径越大,差分过孔阻抗连续性和稳定性越好。
2.2.2 不同形状差分反焊盘仿真结果对比 同等相对尺寸下单端圆形、椭圆形、矩形反焊盘示意图如图4所示,对单端圆形、椭圆形、矩形反焊盘的差分过孔分别进行仿真,仿真结果如图5所示。
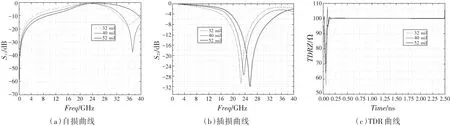
图3 不同直径反焊盘仿真曲线Fig.3 Simulation curves of antipad with different diameter
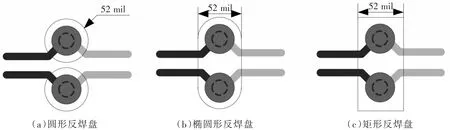
图4 不同形状反焊盘过孔模型Fig.4 Vias model of different shape antipad
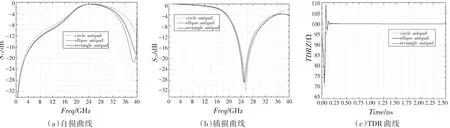
图5 不同形状反焊盘仿真结果曲线Fig.5 Simulation results of different shape antipad
由图5(a)可知,该差分过孔模型在同等尺寸条件下,当频率小于23 GHz时,反焊盘形状为圆形、椭圆、矩形的差分过孔自损S11依次略好;当信号大于23 GHz后,椭圆形反焊盘的自损S11要优于矩形、圆形反焊盘。由图5(b)可知,3种形状反焊盘的差分过孔插损S21比较接近,高频谐振频率并未因反焊盘形状变化而有太大变化,反焊盘形状为圆形、椭圆形、矩形时,其谐振频率依次为24.8、25.2、25.6 GHz,但在谐振频率点圆形反焊盘差分过孔插损比其他两种形状反焊盘差分过孔插损大3~4 dB。由图5(c)可知,反焊盘形状为圆形、椭圆形、矩形时,差分过孔阻抗变化区间依次为[70.25 Ω,100.80 Ω]、[72.55 Ω,108.94 Ω]、[73.33 Ω,108.30 Ω],相对于差分过孔100 Ω参考阻抗值,变化幅度最大百分比分别为29.75%、27.45%、26.67%,且差分过孔反焊盘面积S圆形<S椭圆<S矩形,可见反焊盘面积越大,差分过孔阻抗连续性和稳定性越好。
2.3 眼图仿真
分析不同形状反焊盘对信号传输的影响,采用Designer仿真软件加载差分过孔模型,其中激励源为107个二进制伪随机比特流,传输速率为2.5 GHz,上升时间和下降时间均为100 ps,信号源输出信号幅值为2 V。对直径分别为32、40、52 mil的圆形反焊盘差分过孔,以及宽度为52 mil的椭圆形、矩形反焊盘进行眼图仿真,仿真结果如图6所示。5种结构眼图的眼宽、眼高参数如表1所示。
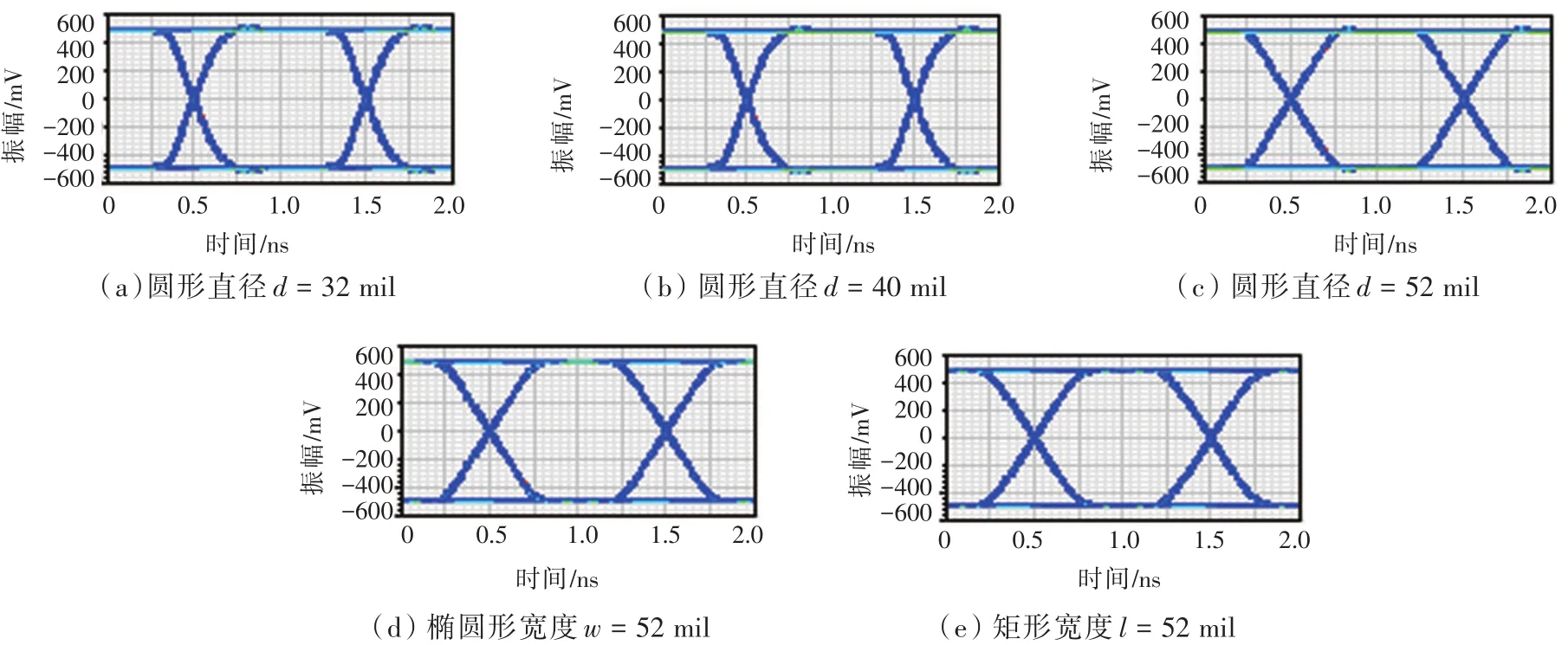
图6 不同形状反焊盘差分过孔信道眼图Fig.6 Eye diagram of differential vias channel with antipad of different shapes
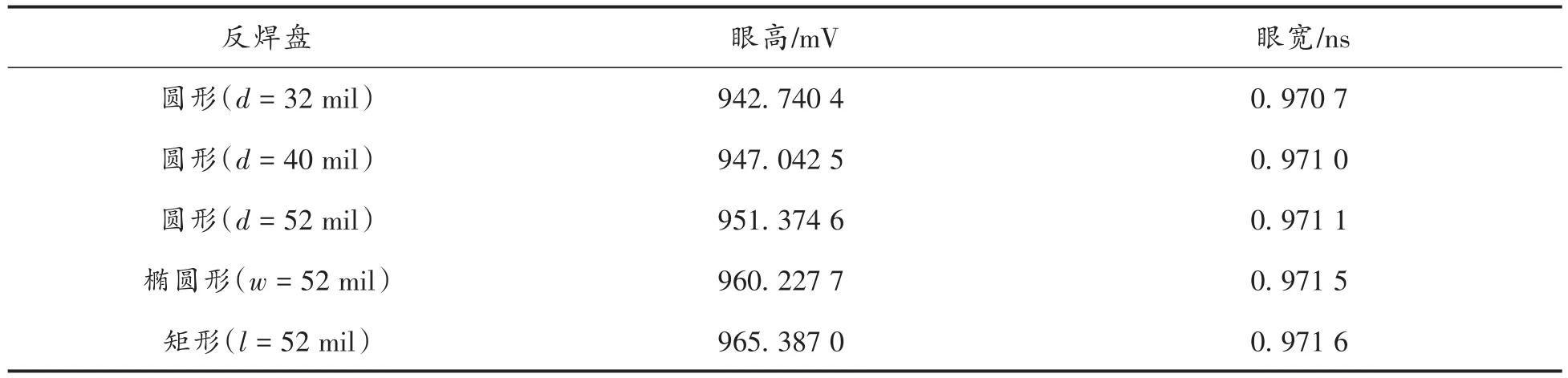
表1 不同形状反焊盘差分过孔信道眼图参数Tab.1 Eye diagram parameters of differential vias channel with antipad of different shapes
从图6仿真结果分析可知,以上参数反焊盘差分过孔眼图仿真结果较为相近,但随着反焊盘面积的增加,仿真接收眼图的眼高、眼宽及眼图质量越来越好。
3 结论
本文通过等效过孔模型进行差分过孔反焊盘参数计算,并根据计算值利用HFSS和Designer全波仿真软件对不同形状反焊盘的差分过孔进行了自损、插损、时域阻抗以及眼图仿真和分析,得到以下几个结论:
1)根据差分过孔模型计算出的反焊盘值,使得差分过孔阻抗更容易控制在合理区间范围内。
2)在一定频率范围内,圆形差分过孔反焊盘直径越大或差分过孔反焊盘面积越大,差分过孔自损、插损、时域阻抗稳定性等高频特性越好。
3)同等相对尺寸下,反焊盘形状为圆形、椭圆形、矩形时,差分过孔自损、插损、时域阻抗高频特性依次略好。在对差分过孔高频特性无精确要求的情况下,设计时可优先考虑常用的圆形反焊盘进行设计。
以上结论为差分过孔反焊盘设计及其高频特性影响分析提供了一定依据,对于高速差分过孔设计具有一定的指导意义。

