数控系统中指令点纠正平滑处理算法
孙树杰,于 东,林 浒,郎言书,3,李备备,3
1(烟台大学 机电汽车工程学院,山东 烟台 264005)2(中国科学院 沈阳计算技术研究所,沈阳 110168)3(中国科学院大学,北京 100049)
1 引 言
在CAD(Computer Aided Design)系统中,模具型腔、汽车发动机和航空结构件广泛采用自由曲线、曲面进行结构描述[1],自由曲面的高速、高精和高质量加工却一直是研究的难点.数控加工过程中,CAM(Computer Aided Manufacturing)系统将自由曲面离散成小线段,生成对应的刀具路径.由于连续小线段之间存在拐角,因此,当数控系统对小线段进行直接加工时,势必引起加速度的频繁波动,降低加工速度,加工过程中刀具的剧烈抖动会在加工件的表面留下多余的刀痕.同时,小线段的拐角会在工件表面留下折痕,影响加工结果的表面光洁度[2,3].因此,需要对小线段表示的加工路径进行平滑处理.
基于遗传算法[4]或蚁群算法[5],对辅助刀具路径进行优化排序,可以减少加工过程中的空行程,但具有最短空行程的刀具路径并不能带来最短的加工时间,同时,无法有效提高加工质量.通过拟合自由曲线、曲面产生的小线段,可以产生平滑的刀具路径.常用的拟合方法包括Akiama样条拟合[6,7]、Cubic样条拟合[8]、NURBS曲线拟合[9-11],这些方法已经应用于西门子[12]、发那科[13]等公司生产的高档数控机床上,但相关技术未见公开讨论.其中,Akiama样条在拟合过程中可以准确经过刀具路径上的指令点,插补点计算效率高,在刀具路径上的指令点均匀排列时,产生的刀具路径平滑性好,拟合过程具备局部可调性.然而,拟合过程中无法通过控制点的权值进行曲线调节,产生的刀具路径在连接点处仅具有G1连续[6].Cubic样条拟合过程计算量小,但是拟合过程中不具备局部可调性,一个数据点的修改,会影响整条曲线的形状,与此同时,当待拟合区域刀具路径接近直线或曲率较大时,难以获得理想的拟合结果[8].NURBS是数据交换国际标准规定的用于工业产品几何定义的唯一一种自由曲线、曲面[14],广泛应用于数控加工领域.采用NURBS曲线拟合技术可以产生连续性较高的刀具路径,拟合过程中一个数据点的修改不会影响到整条曲线,拟合过程具备局部可调性[15];采用三阶NURBS曲线进行路径平滑,刀具路径即可做到G2连续,获得较高的平滑性[10,11].上述小线段拟合方法均假设刀具路径上的指令点位于CAM系统期望的刀具路径曲线上,并直接对指令点进行拟合,拟合区域包含的刀具路径范围较小,且拟合结果不够平滑.而实际应用中,CAM系统生成的指令点却是位于期望曲线的内外公差范围之内,因此,在拟合刀具路径之前,对刀具路径上的指令点进行修正,可以有效提高拟合区中所包含的小线段长度,并提高拟合结果的平滑性.
2 指令点纠正
2.1 拟合区域判别
根据小线段的长度和小线段间的夹角,可以将刀具路径划分为拟合区域和非拟合区域[16].如图1 所示,刀具路径上存在三个连续指令点Pi-1,Pi和Pi+1,θi为Pi-1Pi与PiPi+1之间的夹角.R为经过Pi-1,Pi和Pi+1三个指点的圆弧的半径,O为该圆弧的圆心.线段Pi-1Pi的长度为li-1,线段PiPi+1的长度为li,圆O上的弦线Pi-1Pi对应的弦高为δi-1,弦线PiPi+1对应的弦高为δi,δi-1与δi表示加工过程中的误差,其表达式如下所示:
δi-1=R(1-cosφi-1)
(1)
δi=R[1-cos(π-θi-φi-1)]
(2)

u为系统允许的最大加工轮廓误差,如果δi-1与δi的值小于u,则指令点Pi-1,Pi和Pi+1为连续刀具路径的一部分.
2.2 圆弧纠正
CAD/CAM系统根据系统允许的最大加工误差,将自由曲面、曲线离散成由小线段表示的数控程序.在这个过程中,

图1 双弦高法Fig.1 Bi-chord method
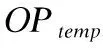
L=2ucosα/(1-sinα)
(3)
圆O存在半径分别为R+u和R的同心圆O′和O″.刀具路径Pi-1Pi、PiPi+1与圆O′分别相交于点Q2i和Q2i+1,则Q2i和Q2i+1为指令点Pi纠正后产生的新指令点.
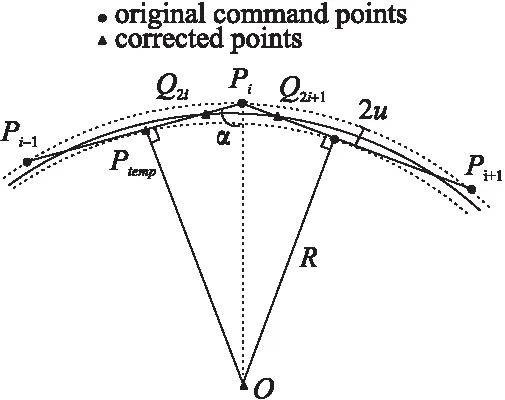
图2 圆弧纠正方法Fig.2 Circle correction method
令l=min(LPi-1Pi,LPiPi+1),如果不等式L≤l成立,点Q2i的坐标表示如下:
(4)
如果L>l,点Q2i的坐标表示如下:
(5)
其中:
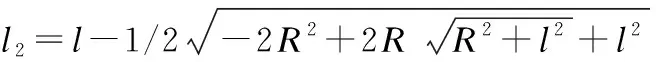
R=l/tanα
l2表示点Pi-1与点Q2i之间的线段长度.
在图2中,点Q2i与点Q2i+1关于OPi对称,因此,根据对称原则,可以得到点Q2i+1的坐标,表达式如下所示:
(6)
2.3 三次样条纠正
与数控程序中给出的指令点相比较,经过圆弧纠正后,刀具路径上非连续区域的指令点更加接近目标自由曲曲面、曲线.
圆弧纠正方法假设相邻指令点的曲率相同,为了进一步对连续区域的指令点进行纠正,采用三次样条方法对刀具路径进行拟合,根据拟合结果,计算修正指令点的坐标,具体步骤如下:
(1)连续区域分段


图3 方向段分段图Fig.3 Division of fitting regions
假设Mi、Mi+1、Mi+2和Mi+3为连续刀具路径上的任意三个连续指令点,M1为连续刀具路径的第一个指令点,则连续刀具路径段分段过程的步骤如下:
1)令i=1,
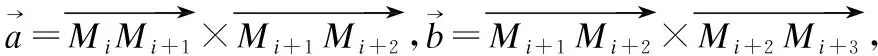

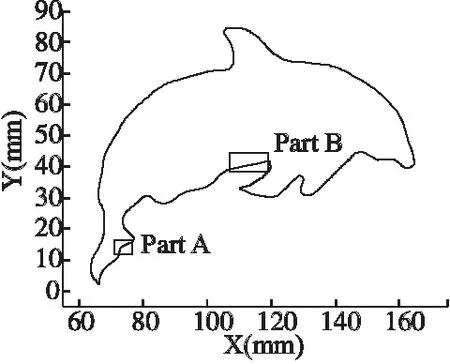
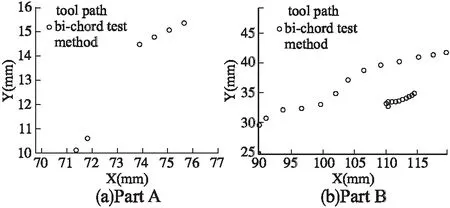
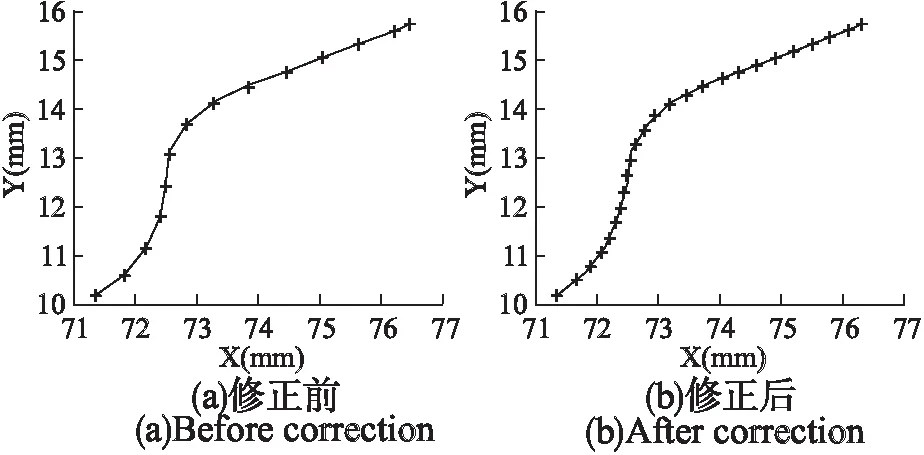
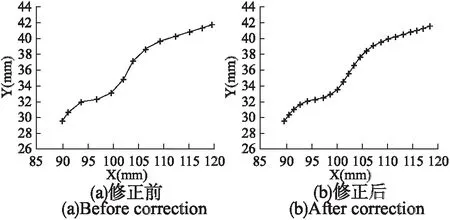
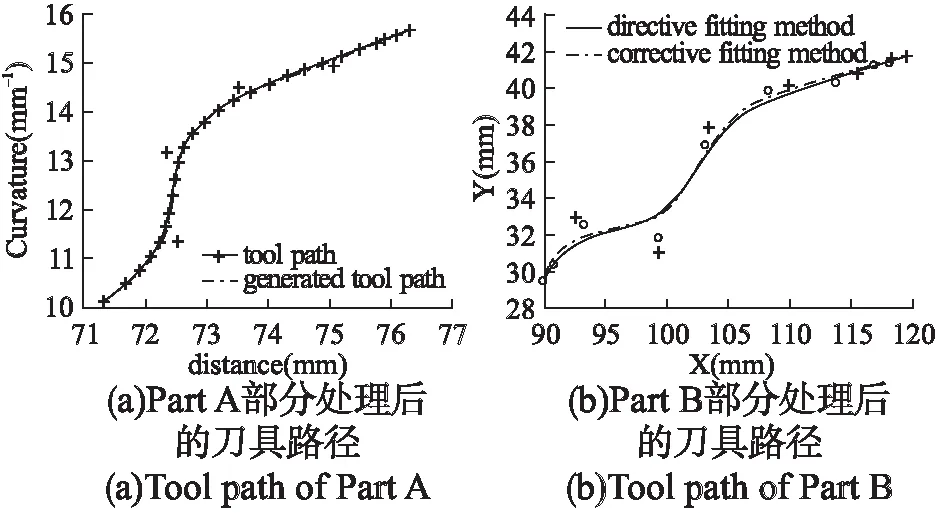
4)如果i 5)结束分段过程. (2)指令点拟合(采用三次样条方法) 图4 三次样条纠正Fig.4 Cubic spline correction method 如图4所示,Mi(i=1…n)为一个方向段内的指令点,C(t)为拟合产生的曲线,其表达式如下: C(u)=Au3+Bu2+Cu+du∈[0,1] (7) 因此,确定系数A、B、C和D后,即可确定曲线C(u),系数A、B、C和D的计算步骤如下: 1)根据M1、M2、M3和M4计算M1点处的切向量C(0)′. A:采用向心参数化方法对点M1、M2、M3和M4进行参数化,即: (8) 其中,ui为指令点Pi处的参数值,li-1和lj-1分别为线段lPi-1Pi和lPj-1Pj的长度 B:假设过点M1、M2、M3和M4的三次样条曲线为C1(u),表达式如下所示: C1(u)=A1u3+B1u2+C1u+d1 (9) 其中,A1、B1、C1和d1的值如下所示: C:则M1点处的切向量表的值为:C(0)′=C1 2)与1)类似,可以求出点Mn处的切向量C(1)′. 3)系数A、B、C和D的表达式如下: (10) (3)计算修正后的指令点(采用迭代方法,并判断纠正结果是否符合加工误差的要求). A 采用向心参数化方法计算方向段内指令点的参数,其中Mmid处的参数为umid. (11) 其中, P=[P1…P(n-1)]T 为了保证加工精度,需要计算指令点与拟合曲线之间的误差[18].如图5所示,Qk是刀具路径上的指令点,C(uk)是该点在拟合曲线C(u)上的对应点. (12) 图5 拟合误差Fig.5 Fitting error 其中,κ是点C(uk)的曲率值,DT和DC表示点Qk在点C(uk)的法平面和切线上的投影,κ、T、N和C的值表示如下: C=(D-DTT)/DC 为了验证算法性能,对图6所示的刀具路径进行处理,在本文中将不经过指令点纠正直接进行拟合处理的算法称之为传统算法. 图6 刀具路径Fig.6 Tool path 图7 拟合区域局部放大图Fig.7 Enlarged view of Part A and Part B 图6中所示刀具路径所含指令点较多,为了简便期间,对图6中方框所示的刀具路径Part A和 Part B进行分析,结果如图7所示. 在图7中,星号表示刀具路径上的指令点,圆圈表示在双弦高误差条件下该部分刀具路径为拟合区域的一部分.从图7可知,Part A部分含有14个指令点,但只有六个指令点符合拟合区域的条件,且这六个指令点分成了两个不相接的部分.Part B部分含有13个指令点,并且完全符合拟合区域的要求. 图8 Part A 部分的指令点Fig.8 Command points of Part A 采用论文中提出的指令点修正方法对Part A和Part B部分的刀具路径进行修正.Part A部分的修正结果如图8所示. 图9 Part B 部分的指令点Fig.9 Command points of Part B 图8(a)为修正前的指令点,图8(b)为修正后的指令点.Part B部分的修正结果如图9所示,图9(a)为修正前的指令点,图9(b)为修正后的指令点.可以看出修正后的指令点对应的刀具路径上,指令点分布更加均匀,刀具路径间的夹角,变化更加平顺.Part A部分的指令点经过修正后,指令点之间的位置关系符合双弦高法的要求,该部分的刀具路径成为拟合区域的一部分. 图10 修正后的指令点Fig.10 Corrected command points 对Part A和Part B部分修正后的刀具路径进行拟合处理,Part A部分处理后的刀具路径如图10(a)所示.可以看出采用传统算法,Part A部分的刀具路径只能采用小线段方法进行表示,其结果如图 8(a)所示,但是采用本文方法,可以将该部分刀具路径拟合成为一个连续、平滑的NURBS曲线,其结果如图10(a)所示. Part B部分处理后的刀具路径如图10(b)所示.其中实线表示原始刀具路径,点横线表示未经指令点纠正后拟合产生的刀具路径,加号表示拟合产生的NURBS曲线的控制点;虚线表示经指令点纠正后拟合产生的刀具路径,圆圈表示拟合产生的NURBS曲线的控制点.在X∈[90,105]的区间内,与传统算法相比,本文算法产生的刀具路径更加平滑. 由于数控程序中的指令点并不是准确的分布在目标曲线上,因此,需要在公差范围内对程序中的指令点进行纠正.本文通过采用圆弧纠正方法和三次样条纠正方法, 1) 有效的扩大了刀具路径上拟合区域包含的路径长度; 2) 使拟合区域指令点分布的更加均匀.仿真分析表明,经过指令点纠正后,刀具路径可以在更大范围内被平滑处理. 对产生的新刀具路径进行平滑处理,仿真分析表明,本文提出的方法拟合产生的NURBS曲线更加平滑.
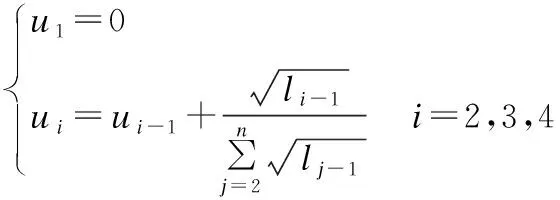
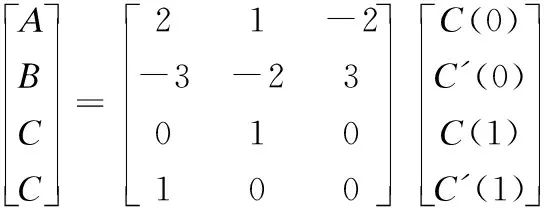
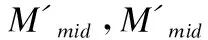
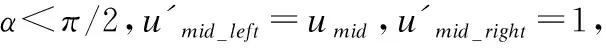
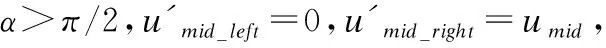
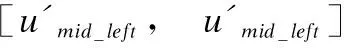
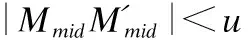
2.4 NURBS曲线拟合


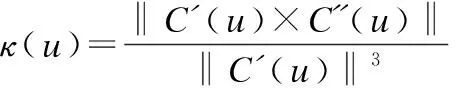

3 仿真分析
4 结 论

