“三门问题”的反思
李 勇 刘 璐
(北京师范大学统计学院 100875)
1 背景
“三门问题”出自美国的电视游戏节目主持人Monty Hall的游戏情景[1],Marilyn vos Savant将游戏情景叙述如下[1]:
假设你在一个游戏节目中,你可以选择三扇门.在一扇门后面是一辆车,另外两扇门后面是山羊.你选了一扇门,比如说1号门,主持人知道门后面有什么,会打开另一扇有山羊的门,比如3号门,他对你说:“你想选2号门吗?”改变你的选择对你有利吗?
该问题的解答,需要比较游戏参与者选中有汽车门的概率.
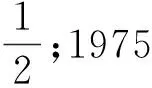
为探索三门问题正确答案,需要用概率语言描述前述游戏情景.目前争论双方都认可如下的概率表述:
① 假设游戏开始前汽车被等概率地放置在每一扇门的后面;
② 游戏参与者初始选择是随机的,即在三扇门中随机地选定其中的一扇;
③ 游戏参与者的选择和汽车的放置是相互独立的;
④主持人对于门后奖品的分布知情,主持人不会打开游戏参与者初始选定的门,也不会打开有汽车的门,只会打开有山羊的门.
在①至④成立的前提下,很多学者利用条件概率的工具“证明”了Selvin Steve结论是正确的,因此这种观点被大多数人接受[3,4,5,6,7,8].
用A1,A2,A3分别表示1,2,3号门后面是车,用B1,B2,B3分别表示游戏参与者打开1,2,3号门,C1,C2,C3分别表示主持人打开1,2,3号门.据我们所知,人们都是基于C3发生的条件概率解决三门问题[3,4,5,6,7,8],而忽略了B1已经发生的情况,其推导有问题.下面我们基于B1C3已经发生的条件下,利用条件概率“解答”三门问题.由①可以确定
(1.1)
由①至③得
由④得
(1.2)
PC3|A2B1=1,PC3|A3B1=0,
因此,游戏参加者打开1号门,并且主持人打开门的概率为
因此游戏参加者坚持选择1号门获得汽车的概率为
游戏参加者改选2号门获得汽车的概率为
=6PA2B1PC3|A2B1
这样就得到与Selvin Steve相同的结论.
目前,大多数学者认可上述证明方法,认为Selvin Steve结论是正确的.本文感兴趣的是上述推导无懈可击吗?主持人的结论错在哪里?引起蒙提霍尔悖论的原因是什么?
2 三门问题的解答
有部分学者指出在三门问题情景中,没有规定主持人是以等概率在游戏者选剩下的有山羊门中选择打开的门,即在实际游戏中公式(1.2)可能不成立.在(1.2)不成立的情况下,上一节中关于游戏者获取汽车概率的计算就是错误的[4].
那么,根据三门问题的实际背景,应该如何计算游戏者获取汽车的概率呢?为此需要用概率语言刻画游戏情境中主持人的行为如下:
⑤主持人在游戏者选剩下的有山羊门中以概率p打开编号最大的门.
在条件①至⑤下,可以利用随机变量的知识解答三门问题.为此引入三个随机变量X,Y,Z分别表示汽车所在门的编号,游戏参与者初始选择门的编号,主持人打开门的编号.这样,坚持选择1号门能够获得汽车的概率为
P1=P(X=1|Y=1,Z=3),
转而选择2号门能够获得车的概率为
P2=P(X=2|Y=1,Z=3) .
现在三门问题答案取决于P1和P2大小的比较:如果P1>P2,就应该选择不换门方案,即游戏参与者坚持选1号门;如果P1 依据条件①至⑤,用条件概率知识和全概率公式可以计算P1和P2,下简述证明过程.对于任意1≤i,j,k≤3,由①和②知 (2.1) 而由③知X和Y相互独立,即 (2.2) 由④和⑤知 PZ=k|X=i,Y=j (2.3) 因此由概率的有限可加性和乘法公式有 PY=1,Z=3 P(Z=3|X=i,Y=1), 将(2.1), (2.1)和(2.3)带入上式得 (2.4) 利用概率的乘法公式得 PX=1,Y=1,Z=3 =PX=1PY=1|X=1· (2.5) PX=2,Y=1,Z=3 =PX=2PY=1|X=2· (2.6) 由条件概率的定义,(2.4)至(2.6)式知 P1=PX=1|Y=1,Z=3 (2.7) P2=PX=2|Y=1,Z=3 (2.8) 由于对于任意p∈[0,1]总有 所以对于三门问题,游戏参与者换门获得汽车的概率总是大于或等于不换门获得汽车的概率,即游戏参与者应该采取换门的对策. 在第2节中,我们在①至⑤约束下得到了换门和不换门获得汽车的概率,下面考察该问题的随机模拟结果,其算法步骤如下: a)初始化p=p0,其中p0∈[0,1]为指定的实数,它刻画了主持人打开门的规律; b)模拟密度矩阵为 的随机数10000个,将其存储为10000维向量x,该向量是10000次游戏中汽车摆放门的编号的模拟结果; c)按a)中方法再模拟随机数10000个,将其存储为10000维列向量y,该向量是10000次游戏中游戏参与者最初选择门的编号的模拟结果; d)对于1≤i≤10000,模拟ui~U[0,1],模拟在第i次游戏中主持人打开门的编号 存储10000维向量z,使得其第i分量为zi; e)在x,y,z中,选出满足条件yi=1且zi=3的模拟结果,在选出的结果中计算xi=1的频率F1(坚持选1号门获得汽车的频率),计算xi=2的频率F2(换为2好门获得汽车的频率). 表1给出了p=0.1×k(1≤k≤10)所对应的获得汽车的模拟频率和概率的对比结果,其中p0,P1,F1,P2和F2的含义如前文所示,n是在10000次模拟中出现事件Y=1,Z=3的频数.从中可以看出:模拟出的各个条件频率和相应的条件概率很接近,其原因是模拟结果中满足条件“游戏参加者选了1号门,主持人打开的是3号门”的频数n都已经比较大,使得条件频率能够接近相应概率值的理论计算结果. 表1 游戏参与者获得汽车的概率与频率 三门问题给我们的启示:在用数学知识解决实际问题时,必须用数学语言准确刻画问题情景,即数学抽象要与实际问题背景相一致;在数学抽象中加入了多余的假设,将引发类似于蒙提霍尔悖论一样的问题,这类问题所引发的争论的起因是所加入的假设不同.
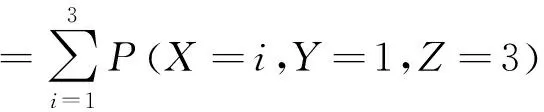

3 三门问题结论的随机模拟验证
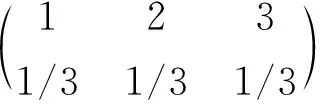

4 引起三门问题争论的原因