T型钢骨混凝土梁动力性能研究

段圣允 （沈阳贵聚建设工程有限公司，辽宁 沈阳 110020）

1 前言

把钢筋混凝土结构和钢结构组合形成的钢骨混凝土结构，与纯钢筋混凝土结构、纯钢结构相比具有许多力学性能上的优点，经常被用作高层建筑、超高层建筑的底部受力构件[1]。

专家学者也从多个方面对T形钢骨混凝土梁的力学性能进行了分析研究。韩建强[2]对实腹式钢骨混凝土T形梁进行静力加载试验，对其设计理论、破坏机理进行了分析；杨松[3]对T型钢骨混凝土梁做了大量往复荷载试验，对构件的延性进行了研究；李明伟[4]通过理论分析，对T梁的正截面抗弯及斜截面抗剪设计公式进行了推导。

T形钢骨混凝土梁现有的研究主要集中在静力荷载方面而对其在动力荷载下性能的研究存在不足，无论是在施工阶段还是在使用阶段冲击现象又经常发生，所以很有必要对其冲击荷载下的动力性能开展研究。文章借助有限元软件ABAQUS对5根2组T形钢骨混凝土梁进行数值模拟，分析T形钢骨混凝土梁在冲击荷载下的动力性能。

2 试件设计

本文共设计了5根2组（一组冲击速度不同、一组边界条件不同）T型钢骨混凝土梁，5根试件的几何参数、配筋完全相同。以冲击速度V=4m/s、两端固定梁为标准工况，构件跨度3000mm，T形梁截面尺寸b×h=150mm×300mm，b′f×h′f=300mm×80mm。腹板下部的纵筋采用强度HRB400、直径12mm的钢筋，并放置2根；翼缘纵筋为强度HPB300、直径10mm的钢筋，共计10根；箍筋采用直径8mm、强度HPB300的钢筋，箍筋间距150mm。内置的T形钢骨采用3块厚度6mm、强度Q235的钢板焊接而成。受力钢筋保护层厚度取为15mm；混凝土强度30MPa。冲击圆柱体重5.5kN，对T梁跨中部位进行冲击。T形构件的横截面如图1所示，数值模型见图2。

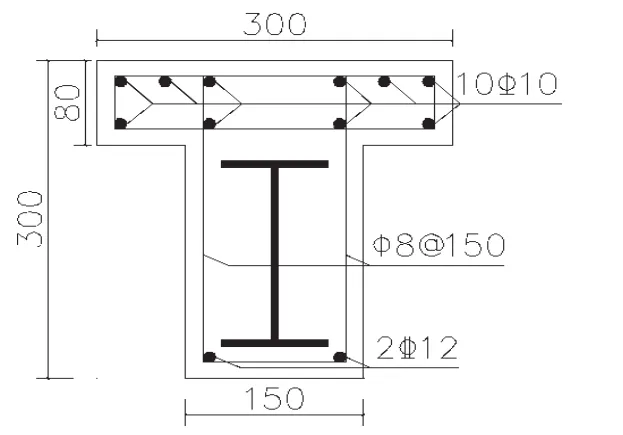
图1 T形梁横截面

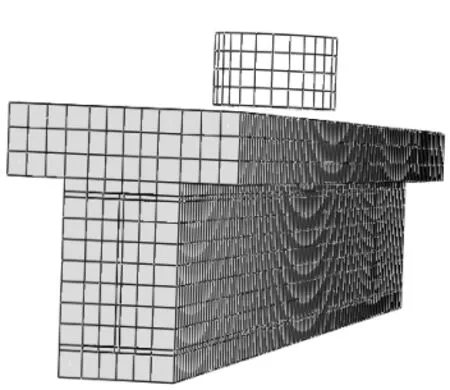
图2 数值模型

3 结果分析

绘制T形钢骨混凝土梁在不同参数下的冲击力时程曲线和位移时程曲线，结果如下。

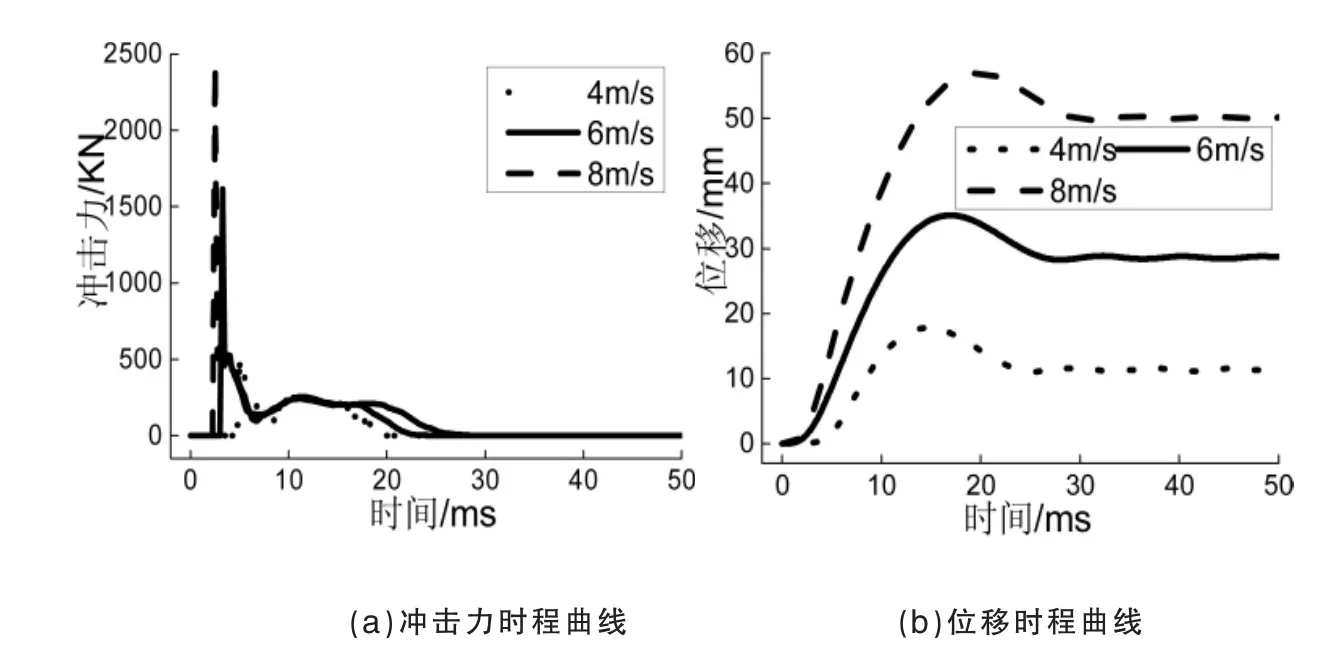
图3 不同速度下的动力性能

3.1 冲击速度的影响

不同冲击速度下的冲击力时程曲线如图3（a）所示。速度取4m/s、6m/s、8m/s时的冲击力时程曲线形状相同，根据形状特点可大致划分成峰值段、平台段、下降段3个不同的阶段；在峰值段，圆柱体下落与T形钢骨混凝土梁接触，冲击力数值由零立刻达到最大，然后又迅速下降；在平台段，圆柱体和T形梁紧贴在一起向下运动，冲击力维持一个数值长时间不变；下降段，圆柱体与T形梁逐渐分离，冲击力下降为零。当冲击速度增大的时候，冲击力峰值也不断增大但上升的幅度不同（462kN、1615kN、2374kN，6m/s、8m/s较4m/s的冲击力峰值分别增加了249.6%、413.9%）；但冲击力平台值都集中在210kN附近，变化不大，相邻速度间的持续时间分别延长了2.8ms、4ms。

由图3（b）不同速度下的T梁跨中位移时间曲线可以发现，速度4m/s时的构件在18.1ms时刻取得极限位移15mm、位移最终残留在11.4mm，速度6m/s和8m/s比速度4m/s的极限位移出现时间延长了15.5%、35.8%，极限位移上升了99.4%、225.7%，残余位移增大了155.5%、352.7%。

3.2 边界条件的影响

冲击速度取为4m/s，边界约束条件不同时的冲击力时程曲线如图4（a）所示。T形梁不同边界条件下的冲击力峰值变化不大，一直在462kN附近波动；一端固定一端简支梁、两端简支梁比两端固定梁的冲击力平台值分别减少了29.6%和49.2%，但平台值经历的时间不断延长。

图4（b）是不同边界条件下的位移时程曲线。由图4（b）可以发现，两端固定梁的跨中位移极值、残余值最小；两端简支梁的跨中位移极值、极值出现时间、残余位移值与两端固定梁相比分别增大了73.9%、53.3%、63.7%；一端固定一端简支梁的位移增长、出现时间延迟均小于两端简支梁。这大概是因为冲击速度一定时，冲击动能固定，固定的支座比简支的支座在冲击过程中要消耗掉更多能量，导致用于跨中变形的能量减少。

4 结论

针对施工阶段、正常使用阶段偶然发生的冲击荷载，本文借助有限元仿真软件ABAQUS对T形钢骨混凝土梁在不同冲击速度速度、不同边界条件下的动力性能进行了数值模拟，得到如下基本结论。

①冲击速度对T型钢骨混凝土梁的动力性能影响显著。随着冲击速度的增加，T形钢骨混凝土梁受到的冲击力数值提高，跨中位置变形程度加剧。

②边界条件对T形钢骨混凝土梁的动力性能影响明显。在边界约束条件逐渐弱化的过程中，T形钢骨混凝土梁的冲击力平台值减小，跨中位移增大，但冲击力峰值保持几乎不变。

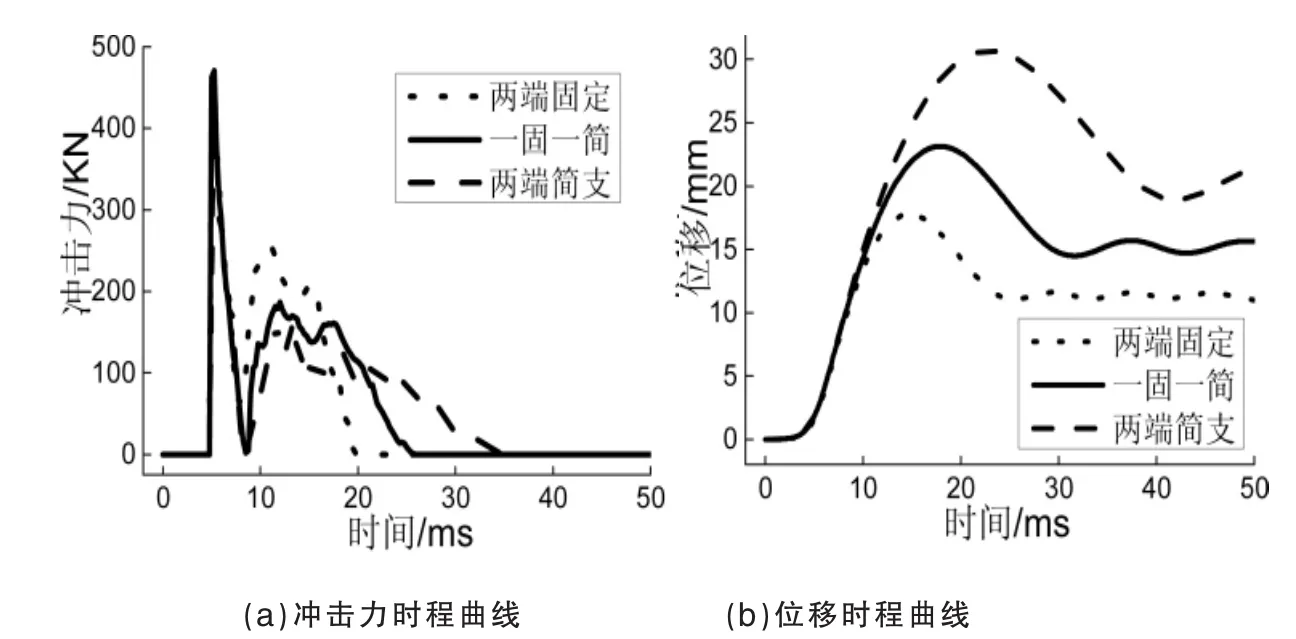
图4 不同边界条件下的动力性能