基于改进RBF神经网络训练算法的蓄电池SOC估算
陈玮匀 杨文伟 陈俊江 胡永乐 覃团发
摘 要: 为了对基站铅酸蓄电池的剩余容量进行估算,在RBF神经网络训练算法中采用梯度下降法结合L1,L2正则化实现隐层节点数的选择。通过模糊控制思想提高泛化能力,引入模拟退火算法减少了需要重复训练的次数。Matlab仿真结果表明,通过改进的RBF神经网络训练算法对蓄电池的电池剩余容量(SOC)估算平均误差达到2%,改进了估算精度的同时也提高了泛化能力并且减少了重复训练的次数。
关键词: SOC估算; RBF神经网络; 正则化; 模糊控制; 模拟退火算法; Matlab
中图分类号: TN245?34; TM912 文献标识码: A 文章编号: 1004?373X(2018)20?0146?04
Abstract: The selection for node number of the hidden layer is realized by adopting the gradient descent method in the RBF neural network training algorithm and combining with L1 and L2 regularization, so as to estimate the remaining capacity for the lead?acid battery of the base station. The fuzzy control idea is used to improve generalization capability. The simulated annealing algorithm is introduced to reduce times of repetition training. The results of the Matlab simulation show that the improved RBF neural network training algorithm has an average error of 2% in SOC estimation of the battery, can improve estimation accuracy and generalization capability, and reduce times of repetition training.
Keywords: SOC estimation; RBF neural network; regularization; fuzzy control; simulated annealing algorithm; Matlab
0 引 言
蓄电池作为基站备用电源设备是供电系统的关键一环,针对通信基站蓄电池管理存在的问题,通过估算电池剩余容量(SOC)估计剩余放电时间,从而制定出最佳的应急发电调度方案。因此建立一种对基站蓄电池剩余容量估算的系统是十分必要的[1]。
目前常用的SOC估算方法有:安时电流积分法、开路电压法以及智能算法[2]等。安时电流积分法由于其依赖初始SOC,会导致多次测量时误差不断积累。开路电压法的测量要求蓄电池处于稳定状态下,而蓄电池从工作状态到稳定状态需要很长时间导致无法及时测量SOC。由于智能算法出色的非线性逼近能力,国内外学者建立了蓄电池SOC估计神经网络[3]模型,早在1999年国外学者利用神经网络来估计蓄电池SOC[4]。综合经济成本和在线估算的要求,本文采取一种改进的RBF神经网络算法,通过仿真实验得到了较好的结果。
1 RBF神经网络
已有的神经网络中大多在结构设计和参数训练上进行改进。径向基(RBF)神经网络因其结构简单可以逼近任意非线性函数的特点而被大多数学者选择并广泛的被应用。RBF神经网络一般由三层构成:输入层,隐含层和输出层。假设对于每个输入样本为n维列向量,即X=(x1,x2,…,xn)T,从输入层到隐含层的映射是非线性的即隐含层的变换函数为一个径向基函数(RBF),故隐含层中第j个神经元(隐含层中神经元)输出为:
式中:E为目标函数;[dp]和[ym]分别为输出层中训练样本的准确输出值和通过神经网络计算后的输出值;N为样本数。
RBF神经网络的性能主要取决于网络的结构,特别是隐层节点数,神经网络越小越好。但过于复杂的网络结构会训练过度导致过拟合[5]而无法取得好的泛化性能。因此选择合适的隐层节点数一直是一门专门的学问[6]。本文使用有稀疏模型能力的L1,L2正则化实现网络结构的隐层节点数选择并结合模糊控制的思想对输入数据适当放缩提高泛化能力。引入具有全局寻优能力的模拟退火算法有效地减少了训练次数,节省了时间。SOC估算误差随着训练误差下降时对比见图1。
2 算法描述
2.1 采用梯度下降法作为神经网络的训练算法
梯度下降训练方法利用梯度搜索技术使得目标函数最小化,在使用梯度下降法训练RBF神经网络的过程中需要定义目标函数E。
2.2 基于L1,L2正则化的隐层节点选择算法
2.3 通过模糊控制对输入数据模糊化提高泛化能力
神经网络的泛化能力是衡量神经网络性能好坏的重要标志,如何提高神经网络的泛化能力一直是该领域研究者不断研究的问题。而通过模糊控制的思想对神经网络输入数据进行适当的缩小从而减小了训练样本和测试样本的差别,提高網络的泛化能力[7]即:[X1-X2
2.4 含有模拟退火思想的梯度下降法
若w表示局部最优解,而W表示全局最优解。首先通过梯度下降法对目标函数进行迭代得到局部最优解[10];然后通过上述算法对所得局部最优解进行处理后会得到一个满足实际需求的新解,即通过上述算法改善了解易陷入局部最小值而需要重复训练的情况。
3 实验结果仿真与分析
3.1 数据准备
本实验的目的是通过采集铅酸蓄电池放电时的端电压和放电电流,并结合蓄电池的SOC对神经网络进行训练得到合适的网络模型。为了检验基于RBF神经网络的SOC估计方法的合理性,本文使用标定工作电压为12 V/150 A·h的铅酸蓄电池进行蓄电池的放电实验,得到一批实验数据作为神经网络的学习样本。一共采集了60组数据,并将其中的45组数据作为神经网络的训练样本,剩余的15组数据作为测试样本。
3.2 训练结果
设定初始隐层节点数为6个。直接使用梯度下降法对其进行适当的训练后,由测试样本对训练好的神经网络进行测试,并得到测试结果如图2所示。采用L1,L2正则化对RBF神经网络进行节点选取,通过选取合适的隐层节点数后其测试结果如图3所示。在上述选取合适隐层节点数目的神经网络基础上,通过模糊控制思想对输入样本数据进行放缩得到测试结果如图4所示。
3.3 实验结果分析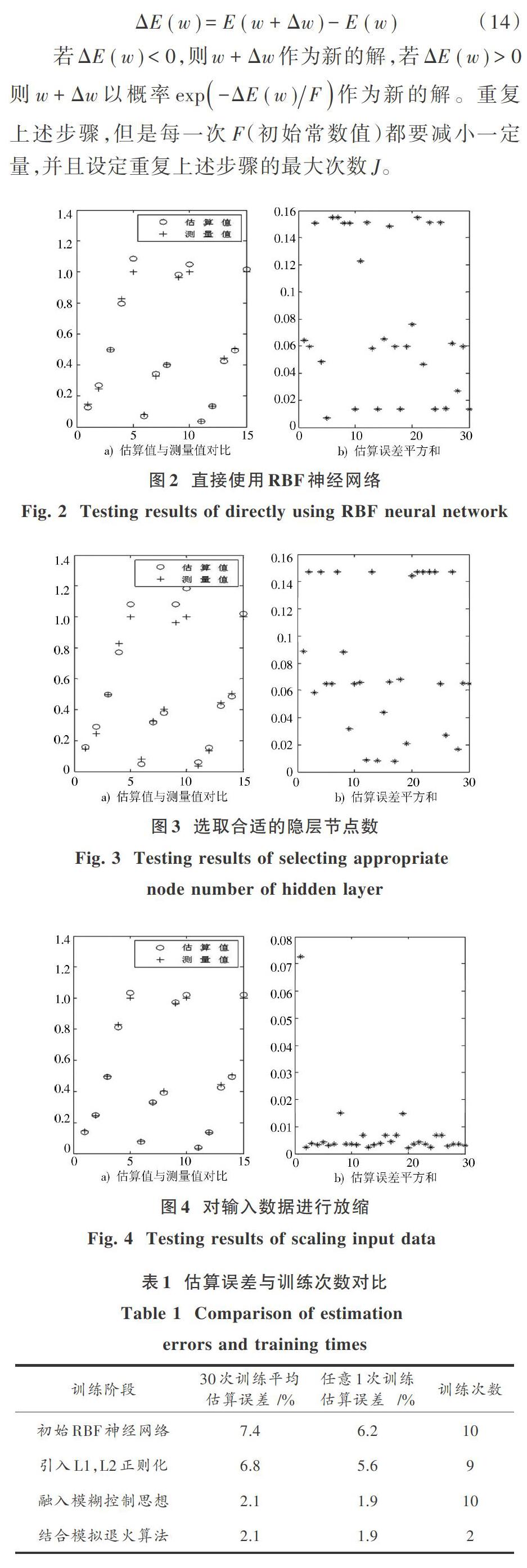
从表1可以看出,在直接采用RBF神经网络进行估算时误差较大,达到7.4%,再通过L1,L2正则化后选取了合适的隐层节点数将误差缩小到6.8%,接着通过模糊控制的思想对输入数据进行一定程度的放缩使得误差达到2.1%,得到一个合适的精度,最后通过模拟退火算法减少了训练所需的次数,大大节省了时间。
4 结 论
本文在对一般的RBF神经网络进行分析的基础上,采用合适的算法解决其存在的隐层节点数目的确定以及泛化能力的提高和训练算法中容易陷入局部最小值的问题。通过实验仿真结果证明上述改进将预测结果误差提高到2%的精度,训练次数也大量减少。由该仿真结果可知,通过以上算法的改进可以提高一般RBF神经网络的估算精度与速度,从而达到了在实际应用过程中的需求。
注:本文通讯作者为覃团发。
参考文献
[1] 潘成举.基于物联网的基站蓄电池运维及应急发电调度系统开发[D].南宁:广西大学,2015.
PAN Chengju. Development of operation maintenance of base station′s battery and emergency generation dispatching system based on Internet of Things [D]. Nanning: Guangxi University, 2015.
[2] 余滨杉,王社良,杨涛,等.基于遗传算法优化的SMABP神经网络本构模型[J].金属学报,2017,53(2):248?256.
YU Binshan, WANG Sheliang, YANG Tao, et al. BP neural network constitutive model based on optimization with genetic algorithm for SMA [J]. Acta Metallurgica Sinica, 2017, 53(2): 248?256.
[3] 曾谁飞,张笑燕,杜晓峰,等.基于神经网络的文本表示模型新方法[J].通信学报,2017,38(4):86?98.
ZENG Shuifei, ZHANG Xiaoyan, DU Xiaofeng, et al. New method of text representation model based on neural network [J]. Journal on communications, 2017, 38(4): 86?98.
[4] WANG Qianqian, WANG Jiao, ZHAO Pengju, et al. Correlation between the model accuracy and model?based SOC estimation [J]. Electrochimica acta, 2017, 228: 146?159.
[5] XU C, LU C, LIANG X, et al. Multi?loss regularized deep neural network [J]. IEEE transactions on circuits and systems for video technology, 2016, 26(12): 2273?2283.
[6] TIAN Yuan, YU Yuanlong. A new pruning algorithm for extreme learning machine [C]// Proceedings of IEEE International Conference on Information & Automation. Macau: IEEE, 2017: 704?709.
[7] SEVAKULA R K, VERMA N K. Assessing generalization ability of majority vote point classifiers [J]. IEEE transactions on neural networks & learning systems, 2017, 28(12): 2985?2997.
[8] LI X, ZHU Y, XIA P. Enhanced analog beamforming for single carrier millimeter wave MIMO systems [J]. IEEE transactions on wireless communications, 2017, 16(7): 4261?4274.
[9] 孟凡超,初佃辉,李克秋,等.基于混合遗传模拟退火算法的SaaS构件优化放置[J].软件学报,2016,27(4):916?932.
MENG Fanchao, CHU Dianhui, LI Keqiu, et al. Solving SaaS components optimization placement problem with hybrid genetic and simulated annealing algorithm [J]. Journal of software, 2016, 27(4): 916?932.
[10] 李珂,顾欣,刘旭东,等.基于梯度下降法的永磁同步电机单电流弱磁优化控制[J].电工技术学报,2016,31(15):8?15.
LI Ke, GU Xin, LIU Xudong, et al. Optimized flux weakening control of IPMSM based on gradient descent method with single?current regulator [J]. Transactions of China Electrotechnical Society, 2016, 31(15): 8?15.

