电网工程预算模型构建研究

刘雪妮

[提要] 电网工程财务集约化建设过程中积累了大量真实、重要、宝贵的业务和财务数据，运用统计分析手段挖掘数据间的内在联系，可以弥补工程财务在科学收集、处理、分析、运用数据方面的差距。本研究从同属性同类型电网工程的形象进度与成本发生的相似性出发，以工程项目的明细账为数据基础，运用多项式曲线拟合的思想，构建出电网工程随时间推移产生的成本轨迹，为该类工程项目构造财务目标曲线。

关键词：多项式曲线拟合；电网工程；预算模型；财务目标曲线

中图分类号：F27 文献标识码：A

收录日期：2018年7月20日

一、引言

在传统电网工程财务管理模式下，预算编制过分依赖于投资计划，甚至出现简单的以计划代预算，导致预算管理严重缺位。随着对电网工程全过程财务管理需求的增加，提升工程項目预算管理效率和效果已成为电网企业更为客观、迫切的需求。在此背景下，本研究以进一步强化投资预算价值导向为目标，坚持业务和财务融合理念，结合基建全过程财务管理目标，尝试构建一套完整的基建项目财务目标曲线管理模式，以有效降低电网项目的造价和投资风险，提高公司投资效益，发挥公司财务价值引领作用。

考虑到同类型同电压等级下的电网工程在建设期间成本的发生会有一定程度的相似性，体现在财务方面就是特定阶段会有一些特定的成本发生，并且依据工程进度情况，总费用支出情况应该也存在一定的相似性。因此，本研究搜集历史期已完工的110kv新建变电站工程为样本，从项目明细账入手，利用最小二乘多项式回归方法对电网项目的各期成本占比随时间推移以及累计成本占比随时间推移情况进行了拟合，以展现工程成本发生的时间趋势状况，构造了该类项目的财务目标曲线。

二、最小二乘多项式曲线拟合方法介绍

最小二乘多项式曲线拟合的原理与实现：最小二乘法多项式曲线拟合，根据给定的m个点，并不要求这条曲线精确地经过这些点，而是曲线y=f（x）的近似曲线y=φ（x）。具体：给定数据点pi（xi，yi），其中i=1，2，…，m。求近似曲线y=φ（x）。并且使得近似曲线与y=f（x）的偏差最小。近似曲线在点pi处的偏差δi=φ（xi）-y，i=1，2，…，m。

多项式曲线拟合不如光滑样条拟合的精度高，但是在曲线拟合时强调对离散点趋势的展现，光滑样条回归要求拟合曲线必须经过相应的点，拟合的曲线会受到异常点的影响，并且最重要的是最小二乘多项式能较好地拟合出曲线并给出相应的函数关系式和误差参数。

三、变电项目总成本曲线模型的构建

项目总成本曲线模型考虑的是项目总成本随着项目周期的时间变化而产生的成本变化。项目总成本曲线模型包括：总成本占比在各期间的发生情况曲线和总成本占比在各期间点的累计发生情况曲线。

在利用最小二乘多项式回归进行成本和时间的拟合之前，需要先完成以下几步：首先，分析各类项目的工程周期和入账周期，以确定合适的成本预测周期；其次，对电网项目周期内的明细账进行月度加总（本研究以每月为一个项目周期内的期间），计算出每个月成本占比；最后，运用最小二乘多项式回归处理实现成本占比与时间的拟合。

（一）总成本占比在各期间的发生情况曲线。利用最小二乘多项式曲线回归对总成本发生占比在各期间情况拟合，具体处理逻辑如下：（1）计算项目每一期（月）发生的总费用；（2）折算每一期（月）总费用在整个项目周期中的占比，每一期总费用占比在项目周期上的总和为1；（3）根据每类项目平均的周期长度，用伸缩法将实际项目时间调整到项目周期范围之内；（4）对所有样本项目在平均周期内各期间的总费用发生比进行平均，取得样本平均各期的总费用发生比；（5）使用Matlab中的多项式曲线拟合方法（Polynomial）为平均总费用占比对时间拟合（区分项目类型*电压等级），得到相应的曲线、回归参数及相应函数关系式。

图1展示了110kv变电站新建项目的成本占比随时间推移呈现的规律性。可以看出，110kv新建项目总成本变化存在先逐步增加，中期后有所减少，项目末期相对增加的趋势。（图1）

多项式曲线拟合得到的参数及函数关系式如下：

Linear model Poly6：

f（x）= p1x6 + p2x5 + p3x4 + p4x3 + p5x2 + p6x + p7 （1）

Coefficients （with 95% confidence bounds）：

p1=9.761e-08 （-2.795e-08，2.232e-07）

p2=-7.528e-06 （-1.773e-05，2.673e-06）

p3=0.0002149 （-0.0001045，0.0005342）

p4=-0.002735 （-0.007562，0.002092）

p5=0.01406 （-0.02196，0.05009）

p6=-0.01148 （-0.1314，0.1085）

p7=-0.0003996 （-0.1303，0.1295）

Goodness of fit：

SSE：0.01332

R-square：0.4166

Adjusted R-square：0.2324

RMSE：0.02648

可以看出R2是0.4166，标准均方差RMSE是0.02648，说明拟合效果尚可。将上述多项式函数式具体化为：

y=1E-07x6-8E-06x5+0.0002x4-0.0027x3+0.0141x2-0.0115x-0.0004 （2）

（二）总成本占比在各期间点的累计发生情况曲线。利用一元线性关系，多项式回归等方法对总成本在各期间点的累计占比进行拟合，以解释度高为选择依据确定最终拟合函数关系式。最终取得110kv变电站新建项目累计总成本占比随时间的曲线、参数及函数关系，具体如图2所示。（图2）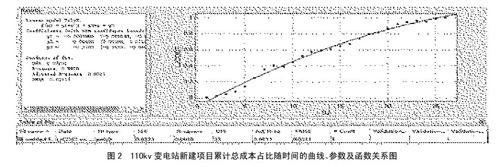

从图2可以看出，110kv变电站新建项目累计总成本占比随时间推移呈现二次式多项式形式，函数关系式可以具体为：

y=-0.0008x2+0.0641x-0.1102 （3）

并且解释度有99.18%。

四、总成本曲线模型下目标值确定及有效性检验

前文从电网项目明细账入手，取得了电网项目成本占比与时间之间的关系曲线和函数，利用普通最小二乘多项式回归，拟合了时间和成本之间的关系。在取得拟合函数的情况下，可以以平均项目周期为自变量X，确定出相应的目标成本占比和累计成本占比，即因变量Y。

由于在利用历史期样本数据拟合成本与时间关系式时，每个样本的周期不同，为了适应统计处理，对所有样本的成本发生周期都依据平均周期进行了缩放处理，因此，在验证模型的有效性时，对于对照样本的成本发生同样需要调整到平均周期才能进行比对。本研究随机选取了某110kv变电站本体工程，将样本实际值和目标曲线勾画在同一坐标系中，这样可以更直观地比较，且实现有效性的直观结论。具体情况如图3、图4所示。（图3、图4）

图3中，散点是某110kv变电站本体工程成本占比实际值，红色曲线是前述利用樣本数据得到的成本占比随时间推移的目标曲线。可以看出，目标曲线基本刻画了散点的变化趋势。说明本研究拟合的目标曲线有参考性。

图4中，蓝色散点是某110kv变电站本体工程累计成本占比实际值，红色曲线是前述利用样本数据得到的累计成本占比随时间推移的目标曲线。可以看出，目标曲线基本刻画了散点的变化趋势。说明本研究拟合的目标曲线有参考性。

五、结语

多年以来，电网工程财务集约化建设过程中积累了大量真实、重要、宝贵的业务和财务数据，通过整合工程全过程的计划、进度、成本、资金等多维度信息，运用统计分析手段挖掘数据间的内在联系，可以弥补工程财务在科学收集、处理、分析、运用数据方面的差距，以提高工程业务信息正确、及时、标准化水平，扭转工程协同管理能力不足的局面，实现财务业务紧密衔接，资金使用安全高效，工程成本归集及时准确，过程监督落实到位，关键风险防范控制有效。

本研究采用了最小二乘多项式曲线拟合方法，从明细账入手将各期成本占比随时间推移以及累计成本占比随时间推移情况进行拟合，展现了工程项目成本发生的时间趋势状况。这一视角所确立的模型是对各期成本费用占比的预测，是相对数值的预测。采用这种方法，对于新立项的工程项目，能够动态预测成本费用随时间变化的趋势，以便随着时间的推移动态地把握项目的资金进度。

主要参考文献：

[1]赵煜武，陈燕丽.计划和预算执行评估模型的设计与实施——以电网建设项目为例[J].会计之友，2014（31）.

[2]刘勇.如何推进电网基建工程投资预算管理[J].江西电力，2014.38（5）.

[3]卢玉，郑燕，赵彪，唐勇.电网工程建设预算编制与计算标准的跟踪分析系统开发应用[J].能源技术经济，2011.23（8）.