计及需求响应与动态气潮流的电—气综合能源系统优化调度

张伊宁, 何宇斌, 晏鸣宇, 郭创新, 马世英, 宋墩文

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 华中科技大学电气与电子工程学院, 湖北省武汉市 430074;3. 电网安全与节能国家重点实验室(中国电力科学研究院有限公司), 北京市 100192)

0 引言

电—气综合能源系统(integrated electricity-natural gas system,IEGS)是指以电力系统为核心,融合天然气系统的现代能源系统[1-2]。近年来,国内外学者针对IEGS的优化运行,已有一些基础性研究。文献[3]提出IEGS的统一建模框架。文献[4]提出一种考虑多类型储能设备的IEGS规划方法。为提升系统韧性,文献[5]和文献[6]分别提出考虑设备N-K故障的IEGS鲁棒优化运行方法和计及新能源波动的IEGS韧性优化调度方法。

需求响应可引导用户理性用能,合理转移高峰用电以平抑负荷峰谷,对提升电力系统运行效率具有重要作用[7]。文献[8]定义弹性矩阵以反映负荷随电价关系,为价格型需求响应的研究奠定了基础[9]。文献[10-12]分别从用户满意度、需求响应不确定性和风电消纳等方面,研究了价格型响应对电力系统优化调度的影响。如何在IEGS中引入需求响应在国际上尚处于探索阶段。文献[13]在IEGS中考虑需求响应机制,并在文献[14]中进一步考虑需求响应的灵活爬坡能力。文献[15]考虑IEGS中联合循环燃气轮机的需求响应机制,并证明了纳什均衡点的存在。以上研究均只考虑了IEGS中电力侧的需求响应机制,忽略了天然气侧需求响应对系统运行灵活性、可靠性的提升,并且未考虑不同能源之间在用能高峰时的相互替代作用[16]。

IEGS可基于稳态或动态天然气潮流方程进行建模。针对稳态系统模型,文献[17]基于非凸非线性Weymouth气流方程,构建了IEGS稳态模型,并采用牛顿—拉夫逊算法求解。文献[18]采用分段线性化方法将Weymouth方程转化为混合整数线性形式,降低了模型的处理难度。文献[19]提出了基于二阶锥规化(second-order cone programming,SOCP)的IEGS稳态建模方法,提升求解效率。文献[20]采用连续锥优化方法以保证二阶锥松弛的严格性。考虑到稳态建模存在误差,文献[21]提出了基于动态气潮流方程的精确IEGS模型。为求解此复杂时空偏微分模型,文献[22]利用天然气管道的储存能力,消除了偏微分项以合理简化原复杂模型;文献[23]在常规气网节点间增加虚拟节点以精细刻画动态气潮流的空间特性,并基于牛顿—拉夫逊法进行求解,但存在一定效率不高问题。如何精确快速求解动态天然气潮流方程是目前IEGS的研究热点之一。

针对上述问题,本文在IEGS中引入价格型和替代型需求响应,精细化描述同种能源的时迁作用和不同能源的替代作用,并采用严格锥松弛技术,快速精确求解含动态天然气潮流方程的复杂IEGS模型。

1 电—气综合能源系统动态建模

本文所提IEGS优化调度模型旨在满足电力和天然气系统安全约束的前提下,实现系统经济性的最优。目标函数式(1)为最小化系统运行费用,包括非燃气机组启动费用、非燃气机组运行费用和系统供气费用。

(1)

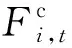
1.1 电力系统约束

1)非燃气机组运行费用

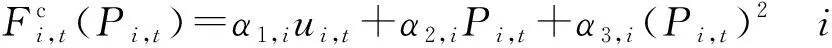
(2)

式中:α1,i,α2,i,α3,i分别为各次项参数;ui,t为0-1整数变量,表示机组i的启停状态。式(2)采用机组费用二次模型。

2)机组运行状态约束

ui,t-ui,t-1=yi,t-zi,t

(3)

yi,t+zi,t≤1

(4)

式中:yi,t和zi,t为0-1整数变量,表示机组i在时段t开机或停机,且机组不能同时启动和停止。

3)非燃气机组启动费用

SU,i,t=SUC,iyi,ti∉NGU

(5)

式中:SUC,i为开启非燃气机组i的耗费。

4)机组出力约束

(6)

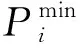
5)机组爬坡约束

(7)

(8)

式中:RU,i和RD,i分别为每小时机组i的上、下爬坡最大值。

6)最小启停约束

用以表征机组需持续开机和停机的最小时段,具体可见文献[24]。

7)电力平衡方程

(9)

式中:fhj,t为线路(h，j)的电力潮流,正负值表示潮流方向;Dj,t为节点j电力负荷需求;CG,j为节点j所连机组集合;CF,j和CE,j分别表示以节点j为起点和终点的线路集合。

8)线路传输容量及节点电压约束

本文研究针对输电网层级,采用直流潮流进行潮流分析,无须考虑电压幅值约束。

(10)

(11)

(12)

θref,t=0

(13)

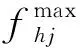
1.2 动态天然气系统约束

本文研究针对树型无环网天然气系统,即管道气潮流方向已确定,这也与实际运行情况相符[20]。天然气潮流遵循流体动力学原理,采用如下约束表征动态天然气系统运行状态[23]。电力与天然气系统通过气转电(燃气机组)和电转气(PtG)设备耦合[6],不失一般性,本文耦合设备主要为燃气机组。

1)燃气机组耗气量

i∈NGU

(14)

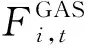
2)燃气机组启动耗气量

SG,i,t=SUG,iyi,ti∈NGU

(15)

式中:SUG,i为开启燃气机组i的天然气耗费量。

3)动态天然气潮流方程

相比分钟级的时间尺度,小时级时间间隔已具有足够分析精度[23],为平衡求解精度和速度,本文将电力系统调度、天然气系统调度和动态气潮流分析的间隔均设为1 h。时空相关的动态气潮流差分方程为：

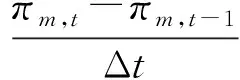
(16)

(17)

式中:πm,t为气网节点m在时段t的气压;gmn,t为管道mn在时段t的天然气潮流,正负表示方向;C1,mn,C2,mn为与管道mn的长度及其他特性相关的参数。过长的管道会给气潮流空间差分方程带来误差,实际建模中可引入虚拟气节点将管道分成多段[23],以更精确地描述动态气潮流的空间特性,但这也会加大计算复杂度。

4)管道储气量方程

动态天然气潮流模型下,由于管道进出口流速不同,管道储气量存在时间耦合关系。

Mmn,t=Mmn,t-1+gmn,t+gnm,t

(18)

式中:Mmn,t为管道mn在时段t的储气量。

5)节点气压约束

(19)

πm,t≥πn,t

(20)

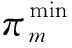
6)天然气平衡方程

(21)

(22)

式中:Lm,t为节点m的天然气负荷需求,包括节点所连燃气机组天然气负荷需求和其他用户的天然气负荷需求Qm,t;CP,m,CS,m,CU,m分别为节点m所连管道、气井和燃气机组的集合。

7)气井供气约束

(23)

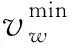
若不考虑节点气压的在时间上的耦合变化,式(16)左侧项为零,可转化为如下稳态天然气潮流方程,管道不具备调节缓冲的能力。

gmn,t+gnm,t=0

(24)

可以看到,稳态天然气潮流建模虽然较为简单,但存在两方面缺陷,一是天然气流速存在明显的时空差异,稳态气潮流建模将气体流速视为恒定,存在一定的计算误差;二是天然气潮流较为缓慢的动态特性可为管道的安全运行提供缓冲,进而扩大综合能源系统运行域,稳态建模无法考虑这种缓冲特性,动态建模更符合实际。

2 综合能源系统的需求响应策略

需求响应可通过改变用户用能行为优化负荷曲线,提升系统运行效率。本文将节点所带用户分为传统用户和能源枢纽两类[16]。传统用户的用能形式固定,其负荷需求按价格敏感程度分为固定型负荷和价格型负荷[10-11];能源枢纽可发挥不同能源形式的替代作用以达到同样的目标,属于替代型负荷[16,25]。考虑到目前能源枢纽的价格响应机制还不明晰,为降低模型复杂度,本文暂不考虑替代型负荷同时受价格响应的情况。

Dj,t=DF,j,t+DP,j,t+DC,j,t

(25)

Qm,t=QF,m,t+QP,m,t+QC,m,t

(26)

式中:Dj,t和Qm,t分别为响应后的节点电力和天然气需求;DF,j,t和QF,m,t分别为电力和天然气固定型负荷;DP,j,t和QP,m,t分别为电力和天然气响应后的价格型负荷,受价格信号影响;DC,j,t和QC,m,t分别为电力和天然气响应后的替代型负荷,表示电力与天然气需求在需要时可以相互转化。不同需求响应策略具体适用负荷可见附录A表A1。

2.1 价格型需求响应

价格型响应是一种用户依据价格信号自发转移用能时段的需求响应方式,系统无须对用户进行补偿[10-11]。价格信号可按时间尺度分为分时电价(1小时)和峰谷电价(数小时)[11],本文采用分时价格以精细分析价格型需求侧响应对调度运行的影响。

下式可得需求响应后的价格型电力负荷需求为:

(27)

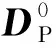
ΔDP,NOR=EELEΔpNOR

(28)

(29)

(30)

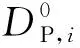
天然气和电力均属重要社会能源,具有相近的市场商品属性。本文进一步考虑价格响应机制在天然气系统中的作用,类比价格型电力负荷,价格型天然气负荷随分时气价变化亦存在如下的关系:

(31)

ΔQP,NOR=EGASΔqNOR

(32)

(33)

(34)

式中:各变量含义可由电力系统价格响应模型类比;EGAS为气量气价弹性矩阵。

价格型负荷可按受价格的影响程度分类,通过数据统计,比较基准日和执行分时价格后相同时刻需求—价格变化,确定各类负荷的价格弹性参数。本文参考美国工业部门分析数据[26],将电力和天然气的自弹性系数分别定为-0.1和-0.2。

2.2 替代型需求响应

部分园区级能源单元已发展为能源枢纽,具有循环燃气轮机、电锅炉、燃气热泵等多类能源转化设备。能源枢纽可优化自身运行方式,选择不同形式的能源,满足终端用户同等质量的用能需求。这种不同能源间的替代作用有利于发挥电—气能源间的互补共济特性,削峰填谷,提升系统灵活性[16,25]。由于替代型需求响应不影响用户用能体验,系统无须对用户进行补偿。考虑到价格型和替代型响应分别表征同种能源间和不同能源间的需求迁移,两者的分析尺度相似,本文将替代型需求响应的分析尺度也定为1 h。对于同一用户的能源需求,其电/气替代型需求响应转化关系如下。

ΔDC,j,t=-γΔQC,m,t

(35)

(36)

(37)

(38)

式中:ΔDC,j,t和ΔQC,m,t分别为替代作用导致的电、气负荷增量;γ为能源转化系数,即单位天然气与电力有效热值之比;We和Wg分别为单位电力与天然气热值;ηe和ηg分别为电力与天然气的能源利用率。本文取γ=0.06 MW·kcf-1(1 kcf=28.317 m3)。式(37)和式(38)对发生替代响应的负荷量进行限制。

(39)

(40)

3 求解方法

本文面向具有单一能源调度中心的综合能源系统,IEGS采用电—气联立求解的方式。由于时空差分方程式(16)的存在,动态模型存在时间耦合关系,求解时需要首先确定合理的气网初始运行状态(t=0)。本文以稳态模型下的t=1 h时刻状态作为动态IEGS模型的初始状态。

由于非凸约束式(17)的存在,稳态与动态IEGS模型均难以直接采用商用求解器求解。目前主流采用牛顿—拉夫逊或分段线性化算法,但求解效率较低。本文采用效率更高的SOCP方法求解,首先将式(17)松弛为易于求解的二阶锥约束:

(41)

引入如下与对应的凹约束保证二阶锥松弛的严格性,使松弛后的解对原问题可行:

(42)

由此,原复杂IEGS模型转化为含有凹约束式(42)的SOCP模型(MISOCP-C)。可采用连续锥优化算法[20]迭代求解。连续锥优化算法(以稳态MISOCP-C模型为例)的详细算法步骤如下。

步骤1:输入系统参数,建立稳态IEGS优化调度模型。

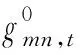
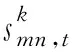
(43)

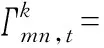
(44)

(45)

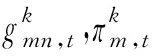
(46)

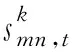
步骤6:重复步骤3至步骤5,直到收敛残差Rk满足以下收敛条件,迭代停止。

(47)

动态MISOCP-C模型求解算法与之类似,但稳态方程式(24)需替换为时空差分方程式(16)。

需要说明的是,由于模型为离散MISOCP,连续锥优化算法的收敛性在数学上无法严格保证。但考虑到所含整数变量相对较少(3×燃气机组数×时段数),且部分已被系统运行约束限制,整数变量可行空间较小。经过初始几次迭代后,整数变量取值已不再变化,此时可固定整数变量,将MISOCP模型转化为SOCP模型,以保证连续凸优化的收敛性。文献[27]也证明了连续锥优化算法对多区多能流优化具有很好的收敛性。

由此,计及需求响应与动态天然气潮流的IEGS优化调度算法流程分为“稳态建模确定初态”和“动态建模求解”两部分,这两部分均采用连续锥优化方法求解,算法整体流程图如图1所示。

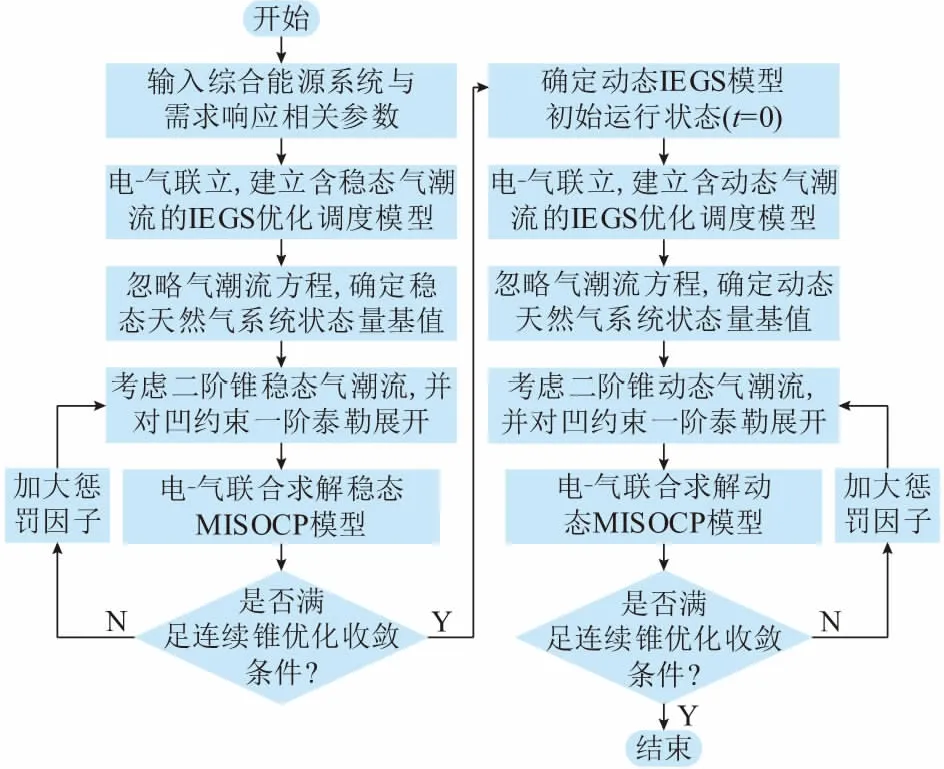
图1 计及需求响应与动态气潮流的 IEGS优化调度流程图Fig.1 Flow chart of optimal dispatch for IEGS considering demand response and dynamic natural gas flow

4 算例分析

4.1 6-6节点系统

以耦合IEEE 6节点电力系统和6节点天然气系统的IEGS进行分析[5,13],验证考虑动态天然气潮流的有效性。电力系统和天然气系统通过3台燃气机组耦合,从天然气系统获取天然气发电并向电力系统供能。系统有2个天然气井、1台燃煤机组、7条输电线路和5条天然气管道。机组参数见附录A表A1,系统接线图和其余设备参数可参见文献[28]。

本文在MATLAB 2014b平台上采用商业优化求解器Gurobi 6.5.0对MISOCP模型进行求解,对比三种不同场景(场景1为气网稳态建模;场景2为气网动态建模,不引入虚拟气节点;场景3为气网动态建模,每条管道引入一个虚拟气节点)。

附录A图A1给出了场景3的求解迭代过程。首先采用连续锥优化方法求解稳态IEGS模型,经4次迭代后稳态模型收敛。之后,选取t=1 h时刻稳态气网状态作为动态模型的初始状态,动态模型经4次连续锥优化迭代后收敛,获得最终的调度结果。随着迭代进行,收敛残差快速达到收敛标准(小于10),二阶锥松弛已严格,调度计划的可行性得以保证。

对比三种场景的调度方案,附录A图A2给出了各场景的机组启停计划,表1比较了各场景费用和计算时间。由附录A图A2可以看到,三种场景下启动的机组数目均呈现与电力负荷相似的峰谷特性。在负荷高峰期(12 ～19 h),所有的4台机组需要全部开启以提供满足系统约束下的负荷供应;在系统负荷需求较低的其他时段,可关闭能耗较高的机组以提升运行效率。对比三种场景,稳态建模下的机组启动数目最多。由于天然气潮流的动态特性可增大系统运行域,在动态建模方式下,场景2可在部分运行时段(2～5 h, 20～21 h)关闭发电能耗较高的4号机组。场景3通过引入虚拟气节点对天然气潮流的动态过程进行了更精细的模拟,管道动态特性对天然气系统运行的缓冲能力得到进一步发挥,可进一步在1 h和6 h时刻关闭高费用4号机组,提升运行效率。

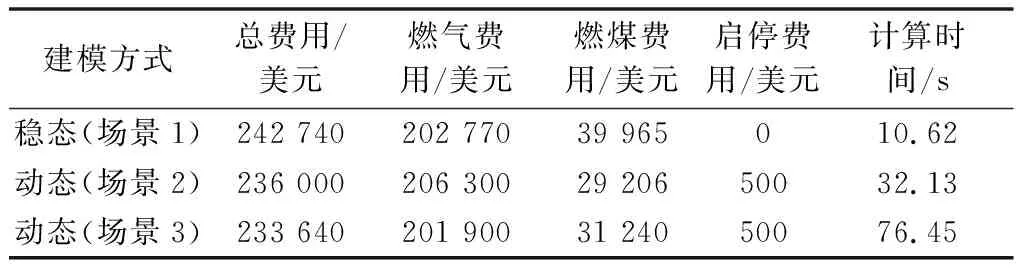
表1 不同建模方式下的系统运行费用比较Table 1 Comparison of system operation cost under different modeling methods

由表1可见,考虑动态气潮流的系统日前调度计划运行费用更低。相比于稳态场景1,场景2和场景3的总运行费用分别降低了2.77%和3.75%。虽然引入虚拟节点有助于对天然气潮流的精细刻画,但由于二阶锥约束数目的增加,计算效率也会降低。如何权衡虚拟气节点数目对IEGS模型的建立具有重要意义,实际中可根据对计算精度和算法速度的要求确定。

附录A图A3比较了不同建模方式下系统管道储气量的变化情况。在稳态天然气潮流模型下,管道出、入口端流速一致,管道储气量维持稳定不变。若将天然气潮流建模为动态,由于考虑了天然气流在时间、空间上的动态特性,同一管道在入口端和出口端的流速并不相同,使得管道具有了天然气调节的能力,管道可作为缓冲环节在需要时储存多余燃气或提供燃气缺额,管道可通过较小的气压差提供相同的天然气流量,节点压力更为稳定。因而相比于稳态建模,基于动态天然气潮流建模的运行可行域更大,系统调度的经济性得到了提升。

4.2 118-10节点系统

以耦合IEEE 118节点电力系统和10节点天然气系统的IEGS为算例进行分析[5,13],验证考虑需求响应策略对系统运行效率的提升。电力系统和天然气系统通过8台燃气机组耦合。系统中有4个节点同时拥有电力与天然气负荷,这些节点固定型、价格型和替代型负荷占比为30%,50%和20%;剩余节点仅拥有电力负荷,固定型与价格型负荷占比为30%和70%。系统基于动态气潮流建模,不引入虚拟气节点以平衡计算精度和效率。系统接线图及设备参数可见文献[29]。

图2比较了需求响应实施前后的系统电力负荷曲线。需求响应实施后,系统电力负荷波动得到了很大程度的平抑,各时段负荷方差从4.30×105降低到3.29×105。这是由于价格型响应将峰时负荷转移到低谷时段,并通过能源替代作用进一步削减了高峰用电负荷,缓解了潮流拥塞,提升了能源输送能力,避免了系统在效率较低的高峰时段运行。

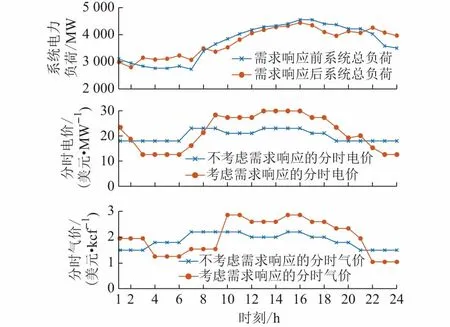
图2 需求响应前后的电力负荷和能源价格比较Fig.2 Comparison of electricity load and energy price with and without demand response

图2还比较了需求响应实施前后的分时能源价格。实施需求响应前的能源价格可根据历史价格信息、能源供给成本、系统拥塞情况等综合得到[10-11]。可以看到,能源价格整体呈现与系统负荷相反的变化趋势。在负荷高峰期(10～20 h),电力与天然气定价均出现了一定程度的上涨,而在负荷低谷期(1～9 h,22～24 h),系统大多倾向于下调能源价格以促进能源消费。注意到,由于互弹性系数的存在,需求和价格间为多时段耦合关系,单纯提高各低谷价格并不能达到系统运行效率的最优,合理提升部分谷时价格(1～2 h)有助于将负荷转移至更低谷的相近时段。但就整体而言,分时能源价格差异经需求响应后被进一步拉大,促使用户整体在峰时少用能,谷时多用能,社会用能方案更趋经济高效。

图3进一步给出了系统价格型和替代型电力负荷在实施需求响应前后的变化。一方面,受增大的分时价格差异驱动,用户调整用能计划以降低费用,各时段价格型负荷波动减小。另一方面,由于系统的电网传输能力在高峰时受限,而气网基本不存在拥塞情况。在电力谷时,用户选择性价比更高的电力能源满足日常需求;在电力峰时,为避免电力系统运行在极限状态,电力替代型负荷被气负荷替代从而降为0。需求响应的引入提高了设施利用率和能源供应安全,保证了IEGS的高效运行。

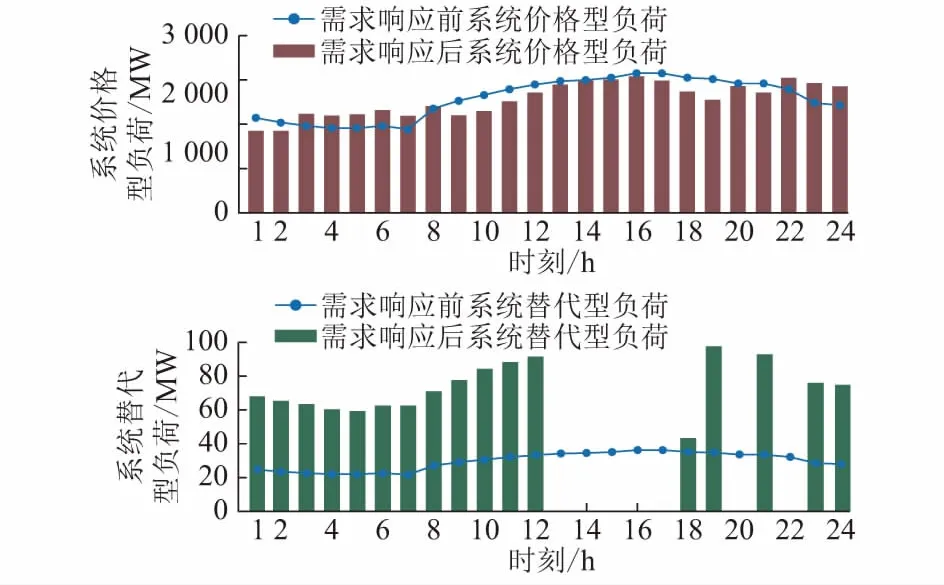
图3 实施需求响应前后的系统价格型 和替代型电力负荷比较Fig.3 Comparison of price-based and alternative electricity load with and without demand response

表2对比了三种需求响应策略(场景1为不考虑需求响应;场景2为仅考虑价格型响应;场景3为考虑价格型与替代型响应)下的系统运行费用。可以看到,需求响应策略的引入可有效提升系统运行经济性。引入价格型响应后,部分高峰负荷被转移到了低谷时段,低耗能机组的发电能力得到充分发挥,总运行费用降低了14 100美元;在引入替代型响应后,用户可选择性价比较高的电能或供应量充足的天然气满足自身用能行为,发挥能源间的互补共济特性,总费用再次降低了1 100美元。由于本系统具有替代型负荷的节点比例较低,替代型需求响应对系统运行效率的提升较小,但可以预想,在未来含较高比例价格型与替代型负荷的综合能源系统中,两类需求响应均对能源的梯级利用有重要作用。

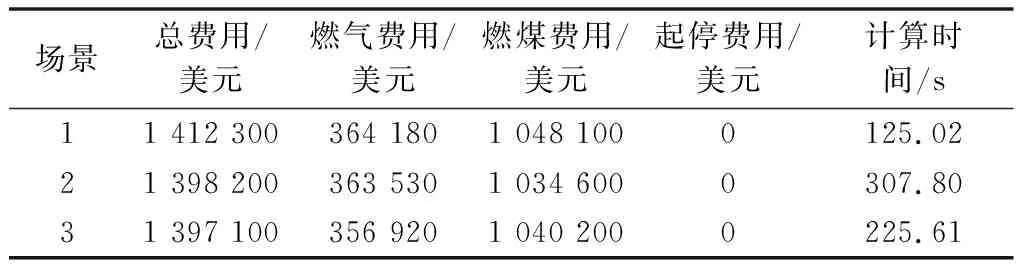
表2 不同需求响应策略下的系统运行费用比较Table 2 Comparison of system operation cost under different demand response strategies

5 结语

本文在IEGS的背景下融入需求响应资源,以优化系统负荷曲线,提升系统的运行经济性。将能源需求响应分为价格型和替代型两类,既考虑了分时能源价格对用户用能策略的引导作用,又考虑了电、气两类能源的互补共济作用。算例测试表明,所提需求响应策略有利于能源需求的削峰填谷和资源整合,可有效提升综合能源系统的运行效率。为对综合能源系统进行精细建模,本文基于动态天然气潮流方程建立非凸优化调度模型。为提升模型的可求解性,将复杂天然气潮流约束进行凸化二阶锥松弛,并采用连续锥优化方法保证松弛的严格性。算例分析验证了所提IEGS动态建模方法的有效性和求解算法的可行性。相比于稳态建模,动态建模可发挥天然气管道的储气能力,降低调度运行费用。

本文所提优化调度模型是对目前IEGS研究的有益补充。下一阶段将重点研究价格型和替代型需求响应耦合机理模型,并基于分布式算法实现电力系统和天然气系统的解耦协调。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。