基于鸟群算法的土壤水分特征曲线模型参数估算*

(山西省水利水电科学研究院，山西 太原 030002)

随着科学技术不断发展，计算机数值计算方法已经成为解决土壤中高维非线性问题的重要工具。水力参数差异是导致土壤水分时空变异的重要因素，而土壤水分特征曲线是关键的土壤水力参数之一。土壤水分特征曲线反映了土壤水分能量和数量之间的关系，是进行土壤水分运动模拟的基础条件。因此，如何精准获取土壤水分特征曲线模型参数对于准确实现水分时空动态预测具有十分重要的意义。

Van Genuchten模型具有较高的预测精度，并且模型参数的物理意义也最为明确，因此，该模型被广泛用于土壤水分特征曲线的定量描述。目前，该模型参数的确定主要包括入渗试验法和数学计算法[1-2]。相对于入渗试验法，数学计算法更加简单方便。但采用前人的数学计算方法进行参数估算时，也存在一定不足。李春友[3]采用单纯形调优法进行了水力参数估算，结果表明该方法会陷入局部最优，因此，它不是一种合适的算法。马英杰[4]采用非线性阻尼最小二乘法进行了水力参数的估算, 但模型预测结果受初始值影响较大，模型精度并不稳定。因此，寻找一种更加合适的算法对于提高Van Genuchten模型预测精度是非常必要的。鸟群算法是一种基于模仿鸟类种群活动过程(觅食、警戒和飞行)而提出的新型全局智能优化算法。该算法具有调节参数少、收敛精度高和鲁棒性能好等优点，在电网优化调度、水库优化调度和年径流量预测等方面取得了较好的应用效果[4-6]，但在农业土壤环境方面未见相关报道。该算法对Van Genuchten模型的参数优化能力及效果也尚不清楚，有待进一步研究。为此，本文将采用该算法对Van Genuchten模型参数进行求解计算和精度评价，以期为Van Genuchten模型参数的估算提供一种新途径。

1 Van Genuchten模型参数求解方法构建

1.1 Van Genuchten模型简介

本文采用Van Genuchten模型对土壤水势与含水率的关系进行描述，具体数学表达式如下[7]：

(1)

式中θ——土壤含水率，cm3/cm3；

h——土壤水吸力，cm；

θs——土壤饱和含水率，cm3/cm3；

θr——土壤残余含水率，cm3/cm3；

α、m、n——土壤水分特征曲线形状参数，m=1-1/n，n>1。

1.2 构造目标函数

由式(1)可知，θs，θr，α和n为4个独立参数。为此，本文构造的目标函数见式(2):

(2)

式中θs——实测含水率，cm3/cm3；

hi——实测含水率θi对应的土壤水吸力，cm；

θ(hi,X)——含水率计算值，cm3/cm3；

X——待求参数向量(θs，θr，α,m)；

N——样本数。

1.3 鸟群(GSA)算法基本思想

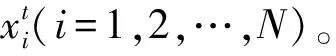
a.觅食行为。通常，鸟类在觅食过程中都需要随时保持警惕性，即觅食行为和警戒行为需要进行切换，并且该过程为一个随机发生过程。这可以用数学语言描述为：在(0,1)范围内，当均匀分布的随机小数小于P[P∈(0,1)]时，鸟群进行觅食，否则，保持警惕。在觅食过程中，每只鸟都能对食物及群体以往最好经验进行及时记录和更新，并且这种群体信息是共享的。这些可以采用数学模型进行描述，见式(3):

(3)

式中j——1,2,…,D;

C——非负常数，认知行为的加速因子；

S——非负常数，是群体行为的加速因子；

Pi，j——第i只鸟最佳位置；

gj——群体当前最佳位置。

b.警戒行为。在警戒行为发生时，个体均会向群体靠拢。由于个体存在警觉性差异，它们向群体中心移动的难易程度也会各不相同，并且在这种移动过程中还会伴随着相互竞争。该警戒行为可采用下式进行描述：

(4)

(5)

(6)

式中k(k≠i)——(1,N)之间的正整数；

a1和a2——(0,2)之间的实数；

PFiti——第i只鸟最佳适应度；

sumFit——鸟群适应度之和；

ε——常数；

meanj——群体第j维平均位置。

c.飞行行为。在鸟群寻找食物过程中必然会发生飞行行为。由于个体差异，个体间的生存能力会存在差异。部分群体能够及时准确发现食物，成为生产者；而另外群体只能跟随生产者获取食物，成为食物索取者。生产者和随机者的出现为随机过程。飞行行为可采用下式进行描述：

(7)

(8)

式中randn(0,1)——服从方差为0，均值为1的Gaussian分布的随机数；

k——(1,N)之间的正整数；

FL[FL∈(0,2)]——索取者会跟随生产者去寻找食物。

另外假设每只鸟会在FQ时间间隔内飞往另一个地方，FQ为正整数。

1.4 Van Genuchten模型参数寻优流程

Van Genuchten模型参数寻优主要包括如下步骤：

步骤1：初始化鸟群规模N、迭代次数M、飞行频率FQ、觅食概率P和常量参数。

步骤2：根据适应度函数计算个体适应度值，并由此确定个体和群体的最佳位置。

步骤3：迭代开始，判断t%FQ是否有余数。

a.有余数，判断鸟群发生觅食行为还是警戒行为。若为觅食行为，采用式(3)更新位置；若为警戒行为，采用式(4)更新位置。

b.若没有余数，判断个体属于生产者还是索取者。若为生产者，采用式(7)更新位置；若为索取者，采用式(8)更新位置。

步骤4：若第i只鸟当前位置优于先前自身最佳位置，则将当前位置更新为自身最佳位置，同时更新鸟群当前最佳位置。

步骤5: 判断是否达到最大迭代次数，若迭代结束转至步骤6; 否则迭代数加1，转回步骤3。

步骤6: 输出鸟群最佳适应度值及鸟群最佳位置所包含的θs，θr，α和n为4个独立参数。

1.5 模型评价

本文主要从模型预测值与实测值的线性一致性、平均相对误差(MAPE)、均方根误差(RMSE)三个方面对模型预测效果进行评价。MAPE和RMSE的计算式分别为：

(9)

(10)

式中WR——试验观测值,mg/kg;

WL——模型预测值,mg/kg;

N——样本数。

2 数据来源

本文采用室内土壤水分特征曲线试验资料对Van Genuchten模型参数进行估算。土壤取样点位于山西省水利水电科学研究院节水高效示范基地。该基地位于太原市小店区，属暖温带大陆性气候区，年平均降水量为495.5mm，年平均气温为9.5℃。土壤经风干、碾压、混合、过筛(筛孔径为2mm)后备用。土壤质地为黏壤土。首先通过压力膜仪法获得土壤水分特征曲线数据资料，然后采用单纯形调优法、非线性最小二乘法和鸟群算法分别对Van Genuchten模型参数进行优化求解。

3 参数估算分析

3.1 Van Genuchten模型参数估算结果分析

本文采用鸟群算法对Van Genuchten模型参数进行求解，获得的最优模型参数见下表。为了进一步评价该方法的可靠性和优越性，采用传统的单纯形调优法和非线性最小二乘法获得的估算结果作为对比，模型参数见下表。由下表可以看出，经单纯形调优法和非线性最小二乘法计算后的土壤饱和含水率(θs)数值相同，获得的土壤残余含水率θr数值也相同。而经过鸟群算法处理后的θr要比前两者结果大11.99%，θs要比前两者结果小0.73%。由此说明，鸟群算法对θr的估算结果影响较大。从形状参数来看，经单纯形调优法和鸟群算法估算后的形状参数α数值相同，而非线性最小二乘法估算结果要比其余2种方法的估算结果高3.08%，由此说明3种方法处理后的α数值差异不明显。由下表还可以看出，经3种方法处理后的形状参数n大小表现为：单纯形调优法>非线性最小二乘法>鸟群算法。相对单纯形法而言，经非线性最小二乘法和鸟群算法估算后的参数n要分别比前者小0.98%和2.00%，说明3种算法对形状参数n的计算结果无显著影响。由下表还可以看出，3种方法估算方法的均方差大小表现为：非线性最小二乘法>单纯形调优法>鸟群算法。综上所述，与传统的单纯形调优法和非线性最小二乘法相比较，基于鸟群算法的参数估算方法主要对Van Genuchten模型中参数θr的影响较大。基于鸟群算法的Van Genuchten模型参数估算方法的结果更加准确。

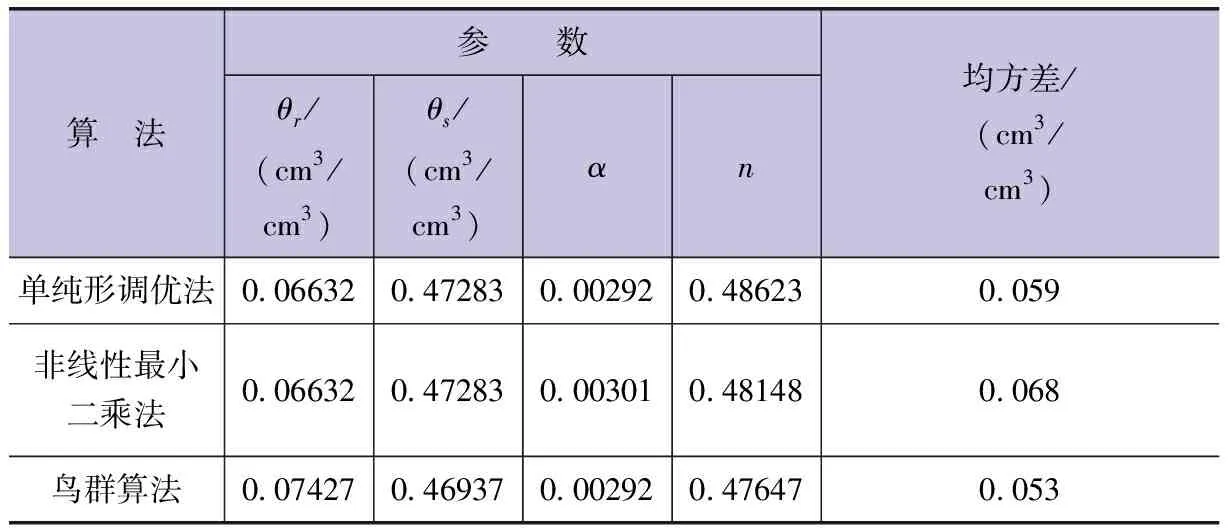
Van Genuchten模型参数估算结果表

3.2 Van Genuchten模型参数估算精度分析

图1为不同估算方法下土壤含水率预测值与实测值间的线性关系。由图1可以看出，经3种算法处理后的估算值与实测值均呈现较好的线性关系。经单纯形调优法、非线性最小二乘法和鸟群算法处理后的线性方程斜率分别为0.904、0.968和0.974，决定系数分别为0.987、0.992和0.996。由此说明，经3种方法处理后，实测值与预测值间线性一致性好坏表现为：鸟群算法>非线性最小二乘法>单纯形调优法。

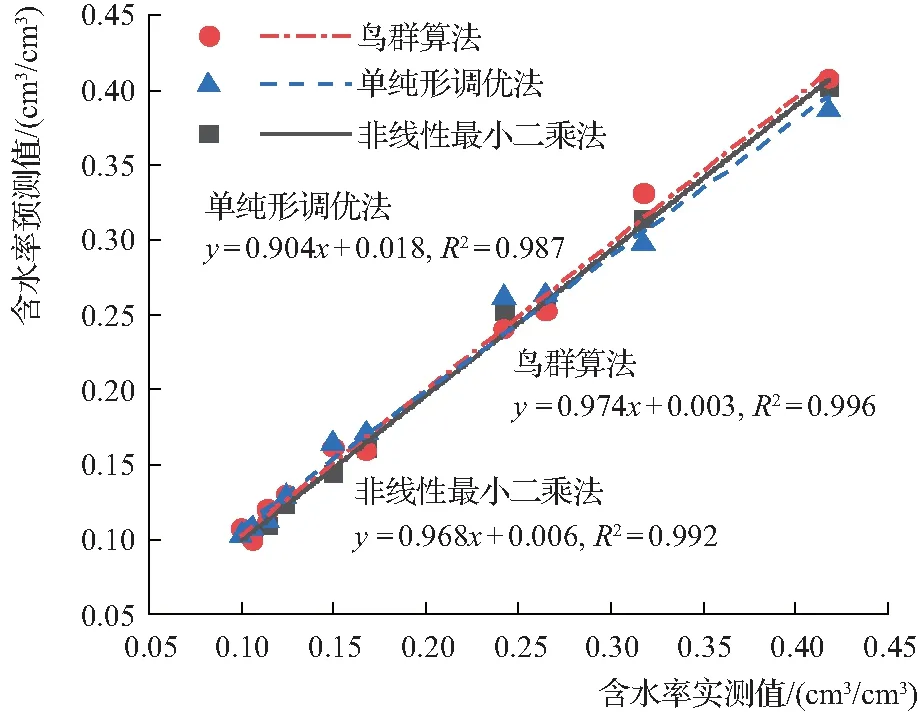
图1 不同估算方法下土壤含水率预测值与实测值间的线性关系

图2为不同估算方法下土壤含水率预测值与实测值对比结果。由图2可以看出，经3种方法估算后的土壤含水率均随土壤水吸力呈指数型衰减趋势。由图2可以看出，在0～2000cm和9000～12000cm范围内，3种算法处理后的结果较为接近，但在2000～9000cm范围内，3种算法处理后的结果差异较为明显。由此说明，不同算法主要对中间土壤水吸力段(2000～9000cm)的土壤含水率预测结果影响较大。从整体上来看，经鸟群算法处理后的含水率预测值与实测值最为接近，单纯形调优法的处理结果次之，非线性最小二乘法的含水率预测值与实测值差异最明显。

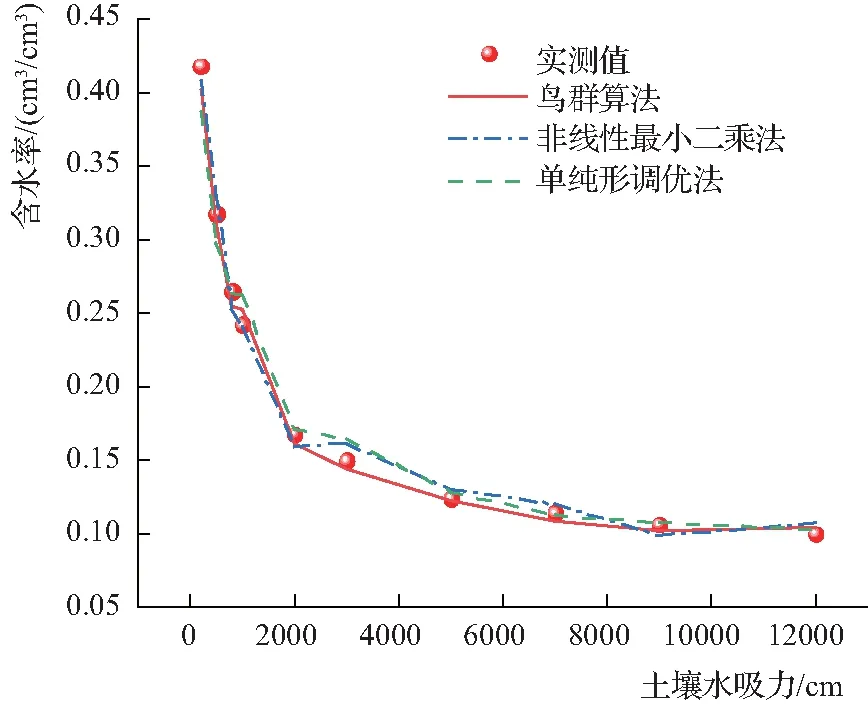
图2 不同估算方法下土壤含水率预测值与实测值对比结果

为了进一步准确比较各种方法的估算效果，有必要对其进行量化分析。图3为不同算法估算值与实测值间的绝对百分误差。由图3可以看出，不同算法处理后的样本误差较为明显。经鸟群算法、非线性最小二乘法和单纯形调优法处理后的绝对百分误差分别为1.00%～4.84%、0.74%～7.78%和0.57%～9.69%，平均相对误差分别为3.50%、4.89%和4.31%。由此说明，不同算法的估算精度好坏表现为：鸟群算法>单纯形调优法>非线性最小二乘法。鸟群算法的估算效果最为理想，单纯形调优法估算效果次之，非线性最小二乘法估算效果最差。

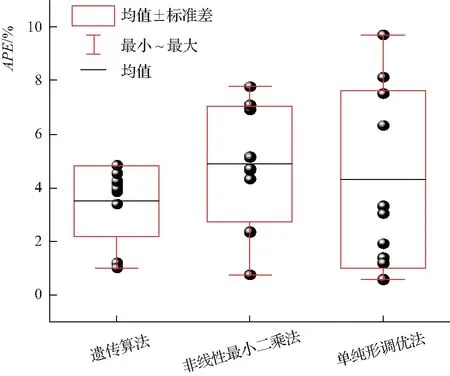
图3 不同算法估算值与实测值间的绝对百分误差

4 结 论

本文通过鸟群算法对Van Genuchten模型中的参数进行了求解，并对参数估算精度进行了评价。与单纯形调优法(SEM)和非线性最小二乘法(NLS)的估算结果相比较，基于鸟群算法(BSA)的参数估算方法获得的土壤残余含水率θr均比前两者要大11.99%。基于鸟群算法的Van Genuchten模型参数估算方法的平均相对误差仅为3.50%，优于传统的单纯形调优法和非线性最小二乘法估算效果。