影响塔里木盆地北缘绿洲非冰期水面蒸发的气象因素分析*

(新疆喀什地区水利水电勘测设计院，新疆 喀什 844000)

蒸发是计算水量平衡的重要内容，其中：水面蒸发是水库、湖泊等水体水量损失的主要组成部分。正确认识水面蒸发与各气象因素之间的关系，对于干旱区水资源高效利用、农田灌溉管理具有重要意义[1]。

塔里木盆地是我国的极端干旱区，降水稀少，蒸发强烈。当地人类活动主要集中在沙漠边缘的绿洲内，平原水库作为绿洲灌区内重要的调节水源，为绿洲工农业生产提供了有效保障。但由于平原水库水深浅、水面面积大、非冰期蒸发损失大，因此如何通过科学合理的调度管理减少平原水库水面无效蒸发，节约宝贵的水资源，将是解决极端干旱区水资源严重短缺的一项重要途径。

赵成义[2]等人以阿克苏绿洲为例，分析了近30年不同口径蒸发器水面蒸发量的变化趋势，表明研究区蒸发量呈下降趋势，水面蒸发量与水汽压差、气温、风速有较好的相关关系，其中影响水面蒸发的主要因子是水汽压差；魏光辉[3]等人以塔里木河下游铁干里克气象站2005年资料为例，采用熵值法对水面蒸发影响因素进行敏感性分析，结果表明温度与风速对水面蒸发影响最为敏感；李万义[4]以水汽压力、风速和相对湿度为主要影响因素，建立了3因子水面蒸发预测模型；滕凯[5]以旬均最高气温、旬均风速、旬均饱和水汽压和旬均日照时间为影响因素，建立了区域水面蒸发预测模型。

由于水面蒸发影响机理复杂，受观测方法精细程度、气候环境变化、观测场地下垫面植被高度与海拔等因素影响，各区域的计算分析结论存在着不同。为探索塔里木盆地北缘绿洲区水面蒸发的主要影响因素，进而为建立该区域水面蒸发预测模型提供技术支持。本文以研究区内的尉犁县非结冰期(2017年5—9月)日水面蒸发量观测数据为例，采用主成分回归方法，对研究区水面蒸发的主要因素进行分析，并取得了一些有价值的研究结果。

1 资料与方法

1.1 数据资料

选取新疆尉犁县气象站2017年5—9月逐日平均气温、最高气温、最低气温、日均风速、日均水汽压、日均相对湿度、日照时数以及日蒸发量(E601蒸发器)8个气象要素资料。

1.2 多重共线性诊断方法

采用方差膨胀因子(VIF)法[6]，诊断自变量(各气象因素)系统中是否存在多重相关性，表达式为：

(1)

式中Ri——自变量对其余自变量Xi进行回归分析的复相关系数；

VIFi>10——各气象因素间多重相关性严重。

1.3 主成分回归方法

主成分分析法(Principal Component Analysis，简称PCA)是利用降维原理，把多指标转化为少数独立综合指标的一种统计方法。

在主成分分析基础上，选取前若干个有效荷载分量，就可建立多元回归模型，进而分析各气象要素指标与水面蒸发之间的定量关系。

2 模型计算

选取日均气温(x1，℃)、日最高气温(x2，℃)、日最低气温(x3，℃)、日均风速(x4，m/s)、日均水汽压(x5，hPa)、日均相对湿度(x6，%)与日照时数(x7，h)这8个因素为自变量；日水面蒸发量(y，mm)为因变量。为保证模型可靠性，本文剔除了有日降水的数据，故模型样本数为140组。

2.1 多重共线性诊断

利用SPSS 13.0软件进行数据共线性诊断，计算结果见表1。由表1可知，各自变量(气象要素)间存在严重多重共线性。

表1 方差膨胀因子

2.2 主成分分析

由于各气象因素量纲不同，所以首先要将原始数据进行标准化处理，之后计算其数据相关性，相关系数矩阵见表2。

表2 相关系数矩阵

注左下角为相关系数，右上角为显著水平，r0.01=0.217。

主成分特征值及贡献率见表3，根据表3确定主成分个数为3(此时，方差累计贡献率为88.0%)。

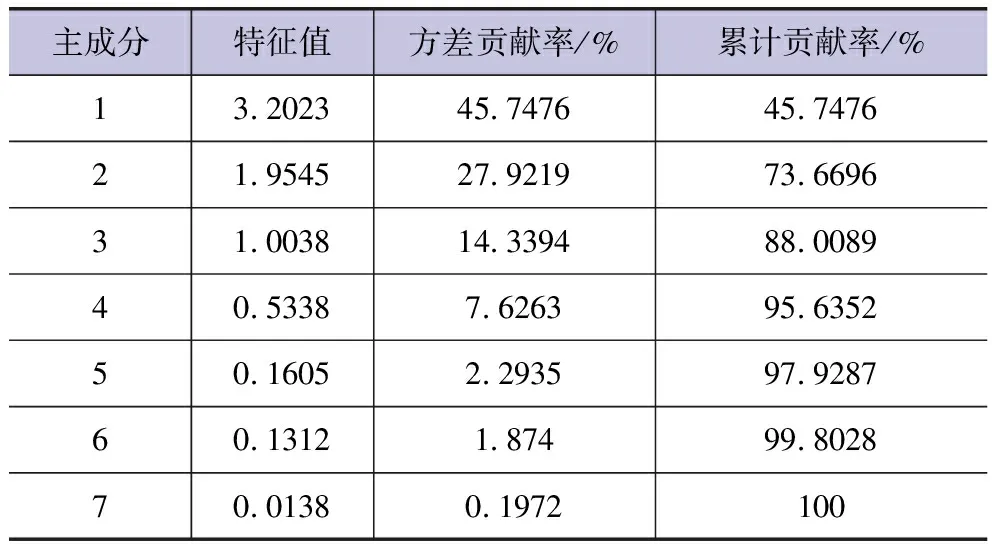
表3 主成分特征值及贡献率

根据确定的主成分个数，采用方差极大正交法求得主成分荷载值(见表4)。

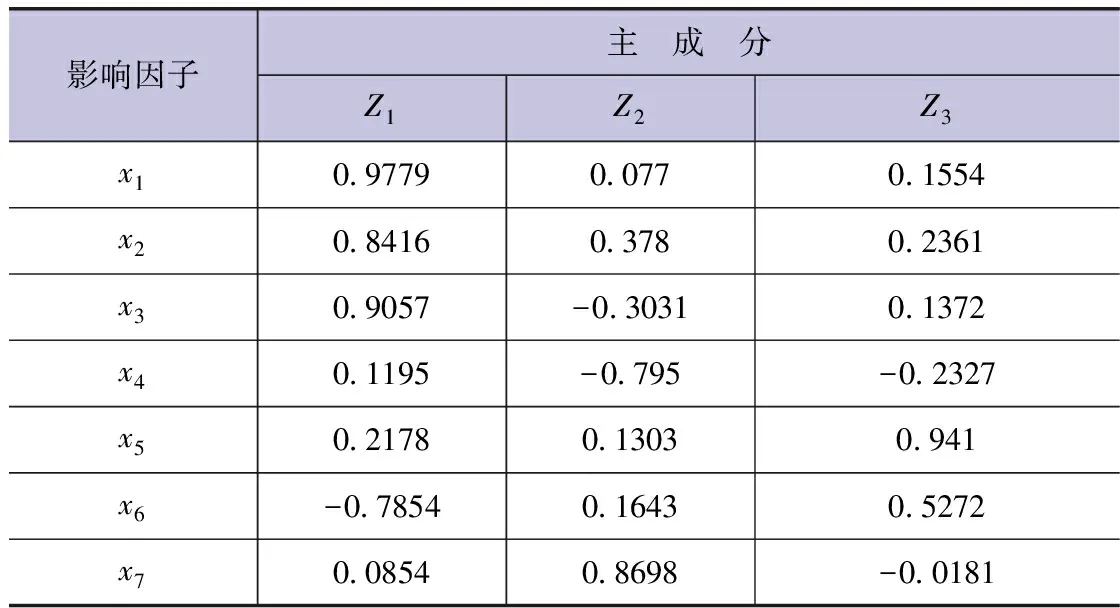
表4 主成分荷载值(不考虑日降水情况)

根据表4可知：第1主成分(Z1)可作为温度与湿度的描述指标，包含了日均气温、日最高气温、日最低气温与相对湿度这4个因素，解释了全部数据信息的45.75%；第2主成分(Z2)包含了风速与日照2个因素，解释了全部数据信息的27.92%；第3主成分(Z3)主要包含水汽压因素，解释了全部数据信息的14.34%。3个主成分包含原有7个指标的88.0%的数据信息。

2.3 主成分回归分析

将上述3个主成分代替原自变量进行回归分析，得到标准化自变量与应变量间的回归模型：

y=10.968+1.151z1-0.735z2-0.447z3

(n=140，r=0.8748，r0.01=0.217)

(2)

式中n——样本数；

r——方程拟合相关系数；

r0.01——显著性为0.01时的方程临界相关系数。

所建主成分回归方程，各回归系数均通过t检验，达到极显著水平(见表5)。

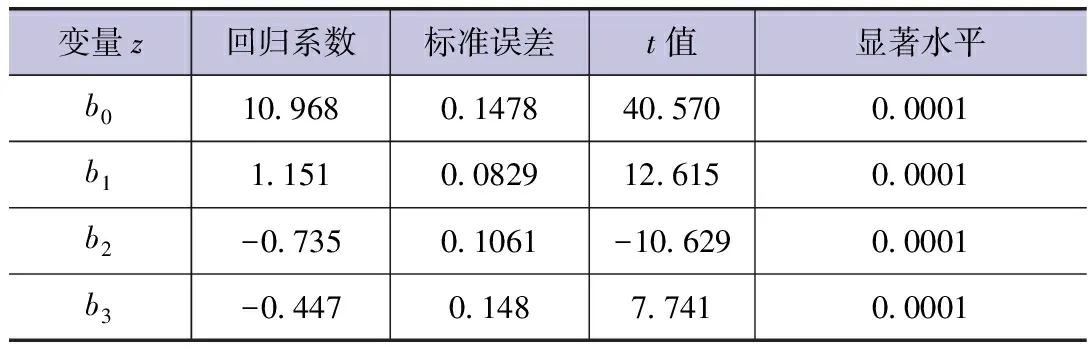
表5 主成分回归方程系数值(不考虑日降水情况)

2.4 日降水情况下的主成分回归模型的建立

为了检验有降水的日数据对主成分回归模型相关参数的影响，将有降水的日气象数据代入上述模型(共计153组观测资料)，经计算得到模型主成分荷载值(方差极大正交法)与回归方程系数值，见表6、7。

表6 主成分荷载值(考虑日降水情况)

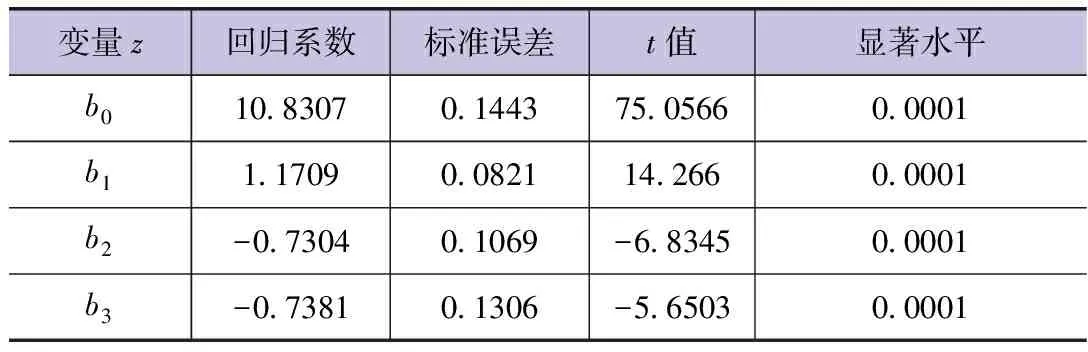
表7 主成分回归方程系数值(考虑日降水情况)

3 结果分析

3.1 不考虑日降水情况下的对比分析

选用不考虑降水影响的140组样本，用7个基本气象要素建立的水面蒸发多元线性回归方程如下：

Y= -7.894+0.936x1-0.059x2-0.301x3+2.119x4-0.213x5-0.001x6+0.175x7(n=140，r=0.9108，r0.01=0.217)

(3)

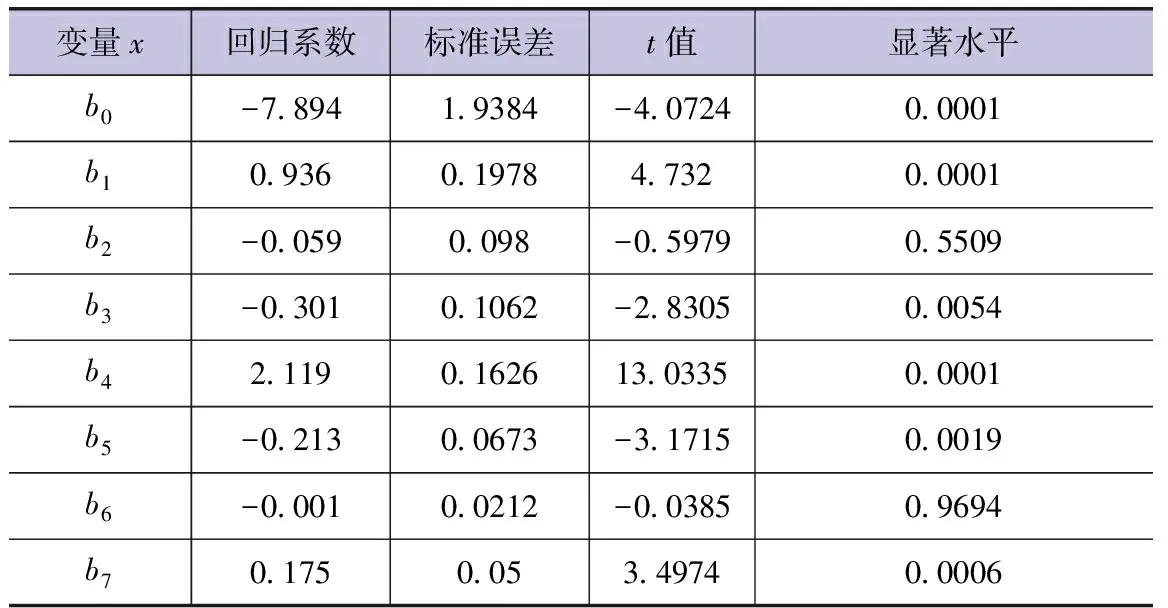
表8 多元线性回归方程系数值(不考虑日降水情况)

由表8可知，式(3)拟合效果优于式(2)，但方程回归系数b2、b6均未通过t0.01检验。而且从方程的物理成因来讲，式(3)中水面蒸发将会随着日最高气温与日最低气温的升高而减小(假设其他气象因素不变的情况下)，与实际情况不符。

3.2 考虑日降水情况下的对比分析

考虑降水影响的153组样本数据，用7个基本气象要素变量建立的水面蒸发多元线性回归方程如下：

Y= -7.207+0.925x1-0.054x2-0.315x3+2.132x4-0.237x5-0.015x6+0.222x7(n=153，r=0.9147，r0.01=0.208)

(4)

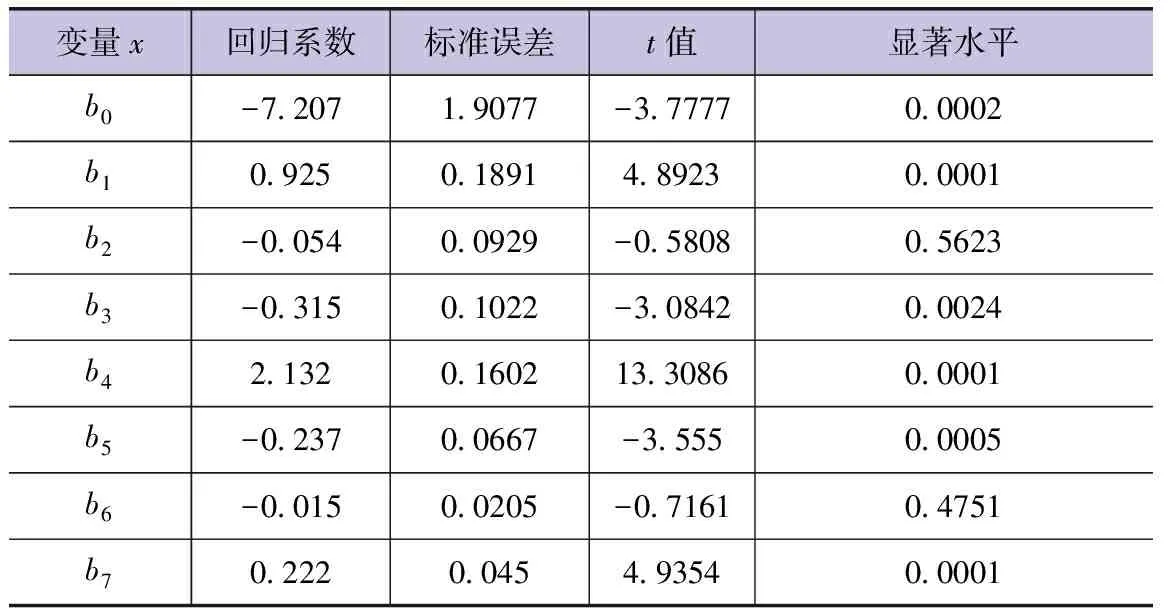
表9 多元线性回归方程系数值(考虑日降水情况下)

由表9可知，方程回归系数b2、b6均未通过显著性检验。且将式(4)与式(3)进行对比可以发现，在考虑日降水的情况下，所建立的模型回归系数数值与原模型有一定出入，但回归系数的正负情况未发生变化。

4 讨 论

a.水面蒸发量影响因素的计算尺度不一样(如采用日、旬、月、年计算尺度)，也会导致主成分分析结果随着计算尺度的变化产生一定的变化。水面蒸发影响因素计算结果在一定程度上还会受数据计算尺度的影响。

b.将日降水数据带入主成分回归模型，会对原模型回归参数的数值大小产生一定影响，但不会影响回归参数数值的正负。同时，由于日降水数据样本数只有13组，剔除日降水数据后的样本数为140组，日降水数据样本占总样本的比例不到10%，故考虑日降水情况时，并不会影响模型在水面蒸发主要影响因素判定上的正确性。

c.气温能直接影响水汽扩散的速度和接纳水汽的能力，气温较高时，水面上的饱和水汽压大，水汽压差大，易于水面蒸发；水面气温高时，水分子运动能量大，水面蒸发强度越大。风速越大，水面上部的水汽压差越大，水汽交换越频繁，水面蒸发就越强烈。相对湿度能反映出空气中的水汽含量距离饱和时的程度和交换的速度。当相对湿度较小时，水汽向外扩散和交换强度增强，蒸发强度越大；相对湿度增大后，既对水面水分子的外逸有抑制作用，也使水汽的扩散和交换强度减弱，蒸发强度减小。因此，本文所得结论合理。

5 结 论

a.本文根据新疆尉犁县2017年非冰期日气象观测数据建立了水面蒸发与主要影响气象因素间的主成分回归模型，该模型通过显著性检验，可用来分析研究区日水面蒸发变化。

b.影响研究区域水面蒸发的主要气象因素为气温、相对湿度、风速与日照时数，这为内陆干旱区水资源合理利用与科学管理提供了理论支持。