高架钢弹簧浮置板轨道减振特性研究及参数优化

程 珊，刘林芽,王少锋

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

城市高架轨道交通以其高效能、准时快捷、低能耗、低污染、安全可靠等突出特点，已广泛运用于城市交通建设中，但高架轨道贯穿城市居民生活工作区，其所带来的环境振动和噪声污染问题越来越不可忽视。钢弹簧浮置板轨道能够减少由轨道传递到高架桥结构的振动能量，有效降低城市高架轨道交通的振动和二次噪声水平，在国内外得到广泛采用。但钢弹簧浮置板价格昂贵，为有效降低工程造价，在设计时优化钢弹簧浮置板轨道的参数就显得十分必要。

近年来，诸多学者已从理论解析、数值计算、实验测试等方面针对浮置板轨道结构的隔振性能进行了大量的科学研究。蒋崇达等[1]建立了钢弹簧浮置板轨道结构的双层梁动力学模型，通过瞬态分析模拟列车移动荷载作用下轨道的动力响应以及轨道系统参数对钢弹簧浮置板动力响应的影响。韦凯等[2]通过建立车辆-钢弹簧浮置板轨道耦合模型，计算分析了扣件刚度和阻尼对钢弹簧浮置板轨道随机振动的影响规律。韦红亮等[3]分别采用有限元和现场试验的方法研究了减振器刚度和间距的改变对高架钢弹簧浮置板轨道结构的振动特性的影响。但以上文献集中于定性分析，并未明确给定设计参数的具体取值范围，尤其是钢弹簧刚度与浮置板密度这两个影响减振效果的重要因素。

本文采用多体动力学与有限元联合仿真的方法，针对这两个参数的变化对高架钢弹簧浮置板轨道减振特性的影响进行研究。

1 计算模型

1.1 计算原理

采用有限元方法分析结构的动力响应，可以得到在移动荷载作用下结构随时间变化的节点位移、速度和加速度的响应，基本方程为

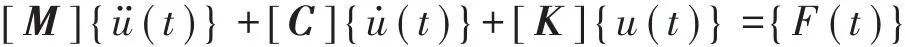
式中：[M]、[C]和[K]分别为结构质量矩阵、阻尼矩阵和刚度矩阵；{ü(t)}、{u̇(t)}、{u(t)}分别为结构振动加速度、速度和位移；{F(t)}为荷载向量。可采用Nemark方法对上述微分方程进行求解。

1.2 研究对象

本文以某城市32 m单箱单室简支混凝土箱梁钢弹簧浮置板轨道作为研究对象，梁高2.8 m，宽13 m，顶板厚度0.34 m，底板厚度0.3 m，腹板厚度0.4 m～0.45 m，翼缘板厚0.2 m～0.5 m。材料性能如表1所示，“桥梁-浮置板-钢轨”结构示意图如图1所示。采用梁单元beam188模拟CHN60型钢轨，网格大小为0.05 m；连接钢轨与浮置板的扣件采用间距为0.625 m的弹簧阻尼单元模拟；箱梁结构和浮置板均采用solid185实体单元进行模拟。

在1/2梁跨断面上，分别在钢轨、浮置板、轨道中心线、翼缘、腹板和底板设置拾取点，拾取列车经过时的加速度信号，如图2所示。

1.3 车辆-浮置板轨道-桥梁耦合模型

为了得到车辆通过时的轮轨力，基于多体动力学理论，利用Simpack软件建立车桥耦合空间动力学分析模型。地铁列车模型的结构参数及动力学参数参照实际地铁A型车选取，其中每一节地铁列车动力学分析模型可认为由1个车体，2个转向架（含4个轮对）等刚体组成，每一节车辆考虑了伸缩、横摆、浮沉、点头、侧滚、摇头6个自由度，轨道不平顺采用美国5级不平顺谱，车辆主要参数见表2。

表1 模型参数

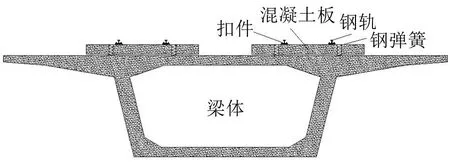
图1 “桥梁-浮置板-钢轨”结构示意图

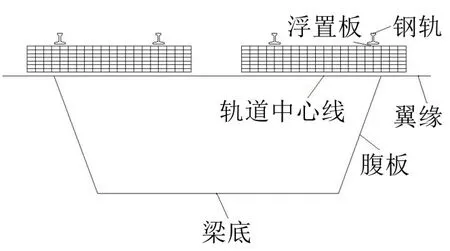
图2 拾取点分布图

将箱型梁有限元模型作为柔性体导入Simpack中，利用Simpack中柔性轨道模块实现桥梁模型和列车模型的共同求解。其中，将桥梁模型和列车模型分别作为两个系统，分别求解轮流迭代。车桥耦合模型之间通过轮轨接触离散点实现位移、速度、作用力的交换。车桥耦合模型如图3所示。

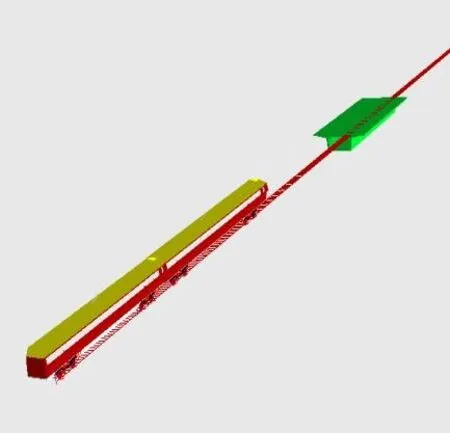
图3 车桥耦合模型

表2 地铁A型车主要参数

基于车桥耦合模型，采用联合仿真的方法，模拟轮轨之间的相互作用力。采用地铁A型车2节编组模拟加载，计算速度为80 km/h，得到的轮轨垂向作用力如图4所示。

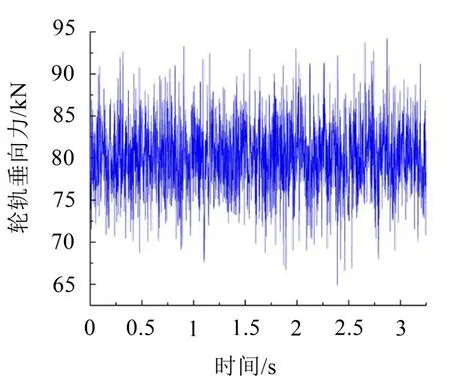
图4 轮轨激振力

2 桥梁振动特性及参数分析

2.1 参数变化对桥梁振动响应的影响分析

对各拾取点的振动时程进行1/3倍频程分析，采用加速度振级的方式分析钢弹簧刚度和浮置板密度变化对轨道和高架桥结构振动水平分布的影响。采用振动加速度级Lva对振动水平进行评价，计算方法如下式

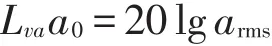
式中：Lva为振动加速度级，单位为dB；a0为基准加速度，取10-6m/s2；arms为1/3倍频程中心频率对应的振动加速度有效值，单位为m/s2。

2.1.1 钢弹簧刚度的影响分析

钢弹簧刚度在6×106N/m～1.2×107N/m范围内变化时，各输出点的振动加速度振级如图5所示。

由图5可以看出：

(1)在2 Hz～20 Hz范围内浮置板的振动水平总体上随钢弹簧刚度的减小而增大，从频域角度分析表明浮置板轨道通过增大自身的振动水平来减小对高架桥振动能量的输入。在40 Hz～200 Hz范围内钢弹簧刚度变化对浮置板振动水平几乎没有影响。

(2)在16 Hz～125 Hz频率范围内，轨道中心线、翼缘、腹板、梁底的振动水平随着钢弹簧刚度的减小而减小，减小值最大达到13 dB。

2.1.2 钢弹簧密度的影响分析

浮置板密度在2 800 kg/m3～3 400 kg/m3范围内变化时，各输出点的振动加速度振级如图6所示。

由图6可以看出：钢轨、浮置板、桥梁的振动水平随着钢弹簧密度增大而减小。密度由2 800 kg/m3增大到3 400 kg/m3时，在10 Hz～20 Hz频率范围内浮置板的振动水平降低约3 dB。

3 钢弹簧刚度变化对浮置板传递函数特性影响分析

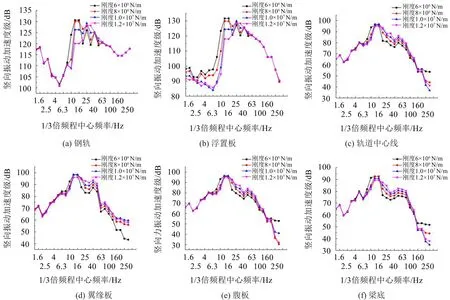
图5 钢弹簧刚度对高架轨道振动水平的影响

振动的传递规律与轨道的结构形式、几何尺寸、材料特性、结构振动的频率等诸多因素有关，是结构的固有特性。传递函数是结构固有特性的一种模型描述方式。传递函数建立在系统频域描述基础上，直接由系统的输入—输出关系获得其数学描述形式，如下

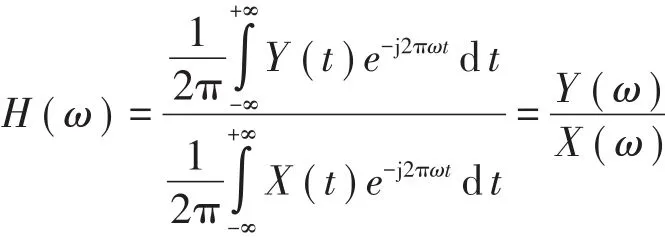
式中：X(t)和Y(t)分别为系统的输入和输出；X(ω)和Y(ω)分别为系统的输入和输出的傅立叶变换；H(ω)为系统的频率特性，即系统的传递函数。

对于高架钢弹簧浮置板轨道系统，选取浮置板上的振动加速度为输入，选取箱梁翼缘、腹板、梁底等处加速度作为输出，来获得不同位置的传递函数。

图7给出了浮置板上的拾取点与翼缘、腹板、梁底拾取点之间的竖向传递函数。

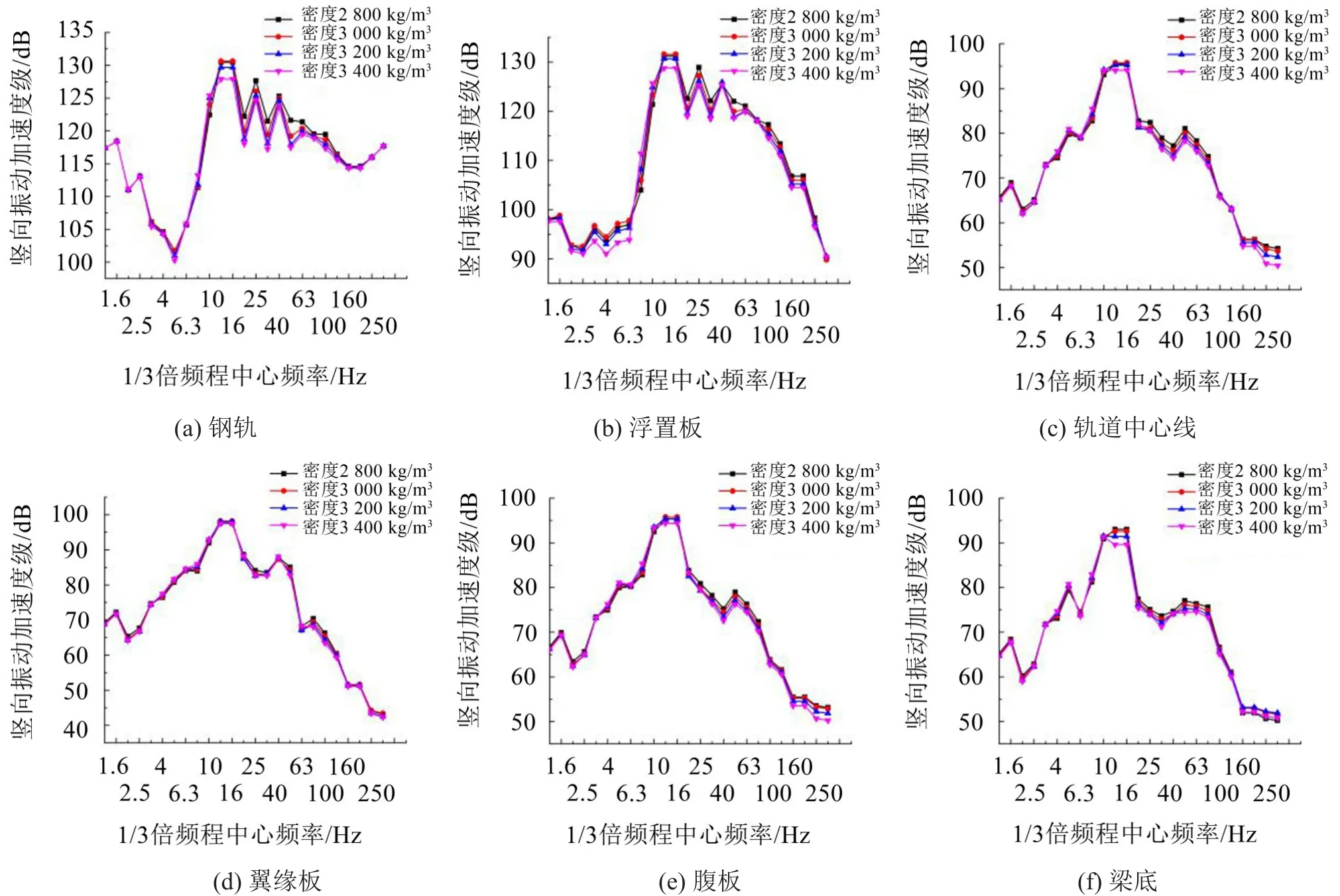
图6 浮置板密度对高架轨道振动水平的影响

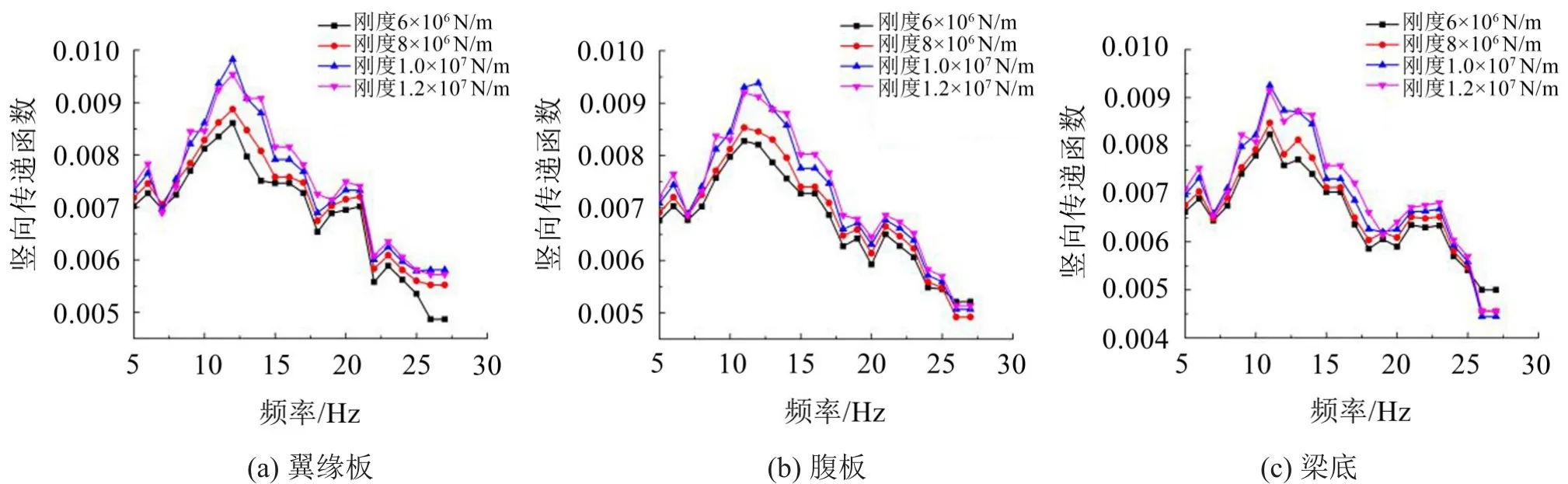
图7 浮置板到桥梁的竖向传递函数曲线

由图7可以看出：从浮置板到翼缘板、腹板、底板的竖向传递函数值均小于0.01，说明浮置板轨道大大降低了钢轨振动向桥梁的传递。钢弹簧刚度的变化对传递函数的影响比较明显，钢弹簧刚度越小，浮置板到翼缘、腹板、底板的竖向传递函数值越小。综合考虑上文钢弹簧刚度变化对桥梁结构振动水平的影响以及对传递函数的影响，在设计浮置板轨道结构时建议将钢弹簧的刚度控制在6×106N/m～8×106N/m比较合适。

4 结语

（1）在2 Hz～20 Hz范围内浮置板的振动水平总体上随钢弹簧刚度的减小而增大，在40 Hz～200 Hz范围内钢弹簧刚度变化对浮置板振动水平几乎没有影响。在16 Hz～125 Hz频率范围内，轨道中心线、翼缘、腹板、梁底的振动水平随着钢弹簧刚度的减小而减小，减小值最大达到13 dB。

（2）钢轨、浮置板、桥梁的振动水平随着钢弹簧密度增大而减小。浮置板密度的增大还可使轮轨相互作用显著减小，延长钢轨使用寿命，但考虑到施工、造价等问题，因此实际设计中要合理设置浮置板密度，建议控制在2 800 kg/m3～3 200 kg/m3比较合适。

（3）钢弹簧刚度的变化对传递函数的影响比较明显，钢弹簧刚度越小，浮置板到桥梁的竖向传递函数值越小。