一种限位器高速转子系统的碰摩行为

白宇杰，姜 磊，杨 璇，吴 雷

（核工业理化工程研究院，天津 300180）

高速旋转的机器在正常工作时，转动与静止的部件不会接触，但在外来冲击作用下，转动与静止的部件之间会发生碰摩，如果引起转子损坏、失稳等，就会造成严重的运行事故。因此，高速旋转转子与静止部件的碰摩，是旋转机械设计中必须考虑的问题。转子碰摩是复杂的动力学现象[1]，也是典型的非线性动力学问题。

从80年代开始，转子碰摩方面有了较多研究。Ehrich[2]采用双线性刚度碰摩模型，研究了Jeffcot转子在不同转速和刚度比下的亚谐、超谐响应和混沌、分岔现象。褚福磊等[3–4]基于油膜支承的Jeffcot转子模型，用直接数值积分法和打靶法研究了转子碰摩的混沌和稳定性，讨论了系统的周期和概周期、混沌和分岔现象。大部分文章主要关注了碰摩转子系统的稳定性，如杜元虎等[5]用延拓打靶法和Floquet理论，研究了油膜轴承转子的分岔现象；袁慧群等[6]由Jacobi矩阵特征值的性质分析了弹性机匣双盘转子系统参数对转子系统解的稳定性的影响。许斌等[7]和徐尉南等[8]认为大多数文献主要关注超过工作转速几倍以上的高转速区域，此时的混沌行为已经充分展开，因此研究了工作转速附近发生的碰摩运动，对同步全周碰摩进行了理论分析，得到了解的存在域和表达式。从文献的梳理和对比中可以发现，多数转子碰摩的研究对象集中在刚性支承的盘轴系统上，且理论研究多，试验研究少。对于戴兴建等[9–10]提出的柔性支承转子系统，其在运行转速下与限位器[11]之间的碰摩特性，受到冲击时的碰摩发展，非常值得研究。

对于柔性支承的高速旋转长转子系统，在外来冲击下转子很可能与限位器发生碰摩，碰摩行为的产生发展和限位器的碰摩刚度与摩擦系数息息相关。本文建立了考虑陀螺效应的柔性支承-刚性转子支承系统模型，在不平衡力的基础上，引入低频简谐冲击力激发转子支承系统的碰摩行为，并分别用数值和试验方法研究了限位器参数对碰摩的影响。

1 动力学模型

图1中的转子支承系统包括了限位器，其主要作用是限制转子在异常工况如冲击下的振动幅值，避免振幅过大引起转子损伤。限位器包括弹性和摩擦两个单元，弹性单元提供碰摩时的动力缓冲和额外支承刚度，摩擦单元实现碰摩时的摩擦系数控制。

对于图1所示的转子支承限位器系统，假设转子为轴对称刚体，只在xy平面内振动，支承特性对称。在系统中存在两个限制振幅的装置，分别是左端支承处的限位体和右端支承处的阻尼。转子的质量为m，极转动惯量为Jp，赤道转动惯量为Jd，上支承刚度为k1，下支承刚度为k2，下支承阻尼为c2，转子左端和限位器碰摩时的刚度为ks，碰摩时的动摩擦系数为μ。整个系统包括转子左端的(x1,y1)和右端的(x2,y2)4个自由度。

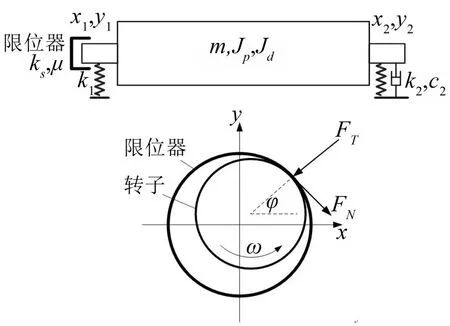
图1 柔性支承转子限位器系统

该转子以角速度ω旋转，转子长度为L，半径为r，上下两端的不平衡质量力矩分别为Ume1和Ume2。根据拉格朗日方法可以得到上述转子限位器支承的控制方程为

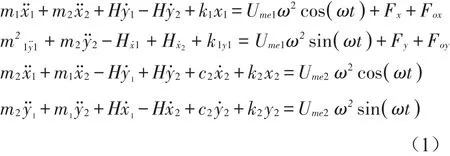
转定子之间的碰摩力有两种模型：一是动量守恒法，忽略碰撞过程，认为碰摩前后转子、定子的位置不变，速度突变，碰摩引起的能量损耗用恢复系数来描述[12]；二是碰摩力模型，假设转子和定子间的碰撞是弹性的，用法向弹性恢复力和切向摩擦力表示碰摩作用。碰摩力模型比动量守恒法能更多揭示物理过程和计算细节，文献也显示碰摩力法更接近试验观测[13]。假设系统左端和限位器的间隙r0，则碰摩力如下所示

转化到直角坐标系中有

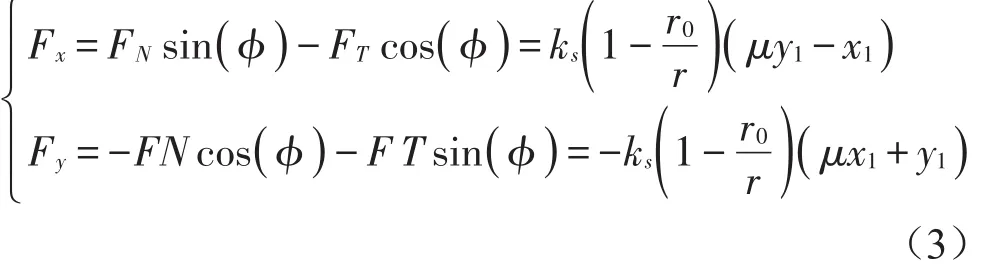
其中：kS是碰摩刚度，μ是碰摩摩擦系数，是径向位移。

为了验证数值计算结果，搭建了图2所示的试验装置。

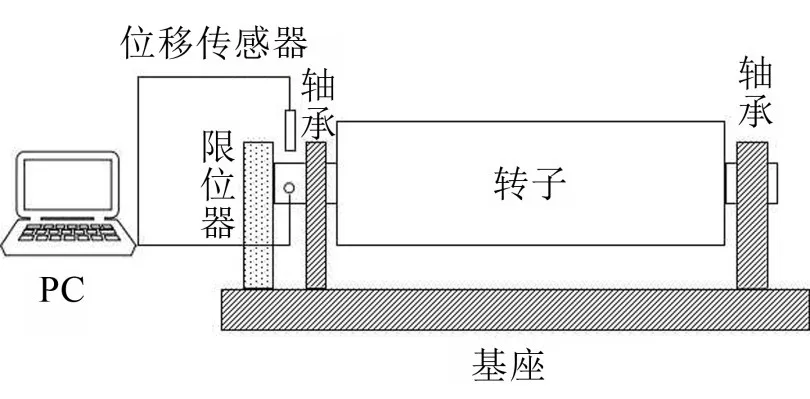
图2 碰摩试验装置

转子放置在左右轴承上旋转，其中左端的轴承刚度较小，转子最左端在限位器的空隙内转动。试验进行时，首先将转子加速到一定的转速下，然后在基座上施加稳定的谐振激励，增大激励强度直到转子最左端和限位器发生碰摩，碰摩发生后停止在基座上施加激励，观察转子和限位器之间的相互作用。试验过程中，用两个正交的电涡流位移传感器检测转子左端的振动信号，并用LMS Test.Lab软件进行数据采集记录和处理。

2 碰摩行为

许斌[7]在研究转速接近第一临界转速时转子的碰摩行为时，提出碰摩后的运动演变有3种可能：一是发生碰摩后又脱离碰摩；二是转子定子之间持续碰摩，且转子以自转角速度贴着定子内壁打滑回旋，称为“同步全周碰摩”；三是呈现出“花瓣形”的运动轨迹，这是Hopf分岔。对于图1中所示的转子支承限位器系统，随着碰摩参数不同，同样存在不同形式的碰摩演变。值得注意的是，本文为了尽可能得到所有的碰摩行为，在数值计算中并没有限制碰摩摩擦系数的取值范围，因此在小碰摩刚度时，会出现摩擦系数过大，不符合实际的情况。在此主要研究不同碰摩参数下的不同碰摩行为，摩擦系数数值大小的实际意义不明显。

碰摩刚度1×103N/m时的轴心轨迹如图3中(ac)所示，包括0.5、0.6、0.8三个摩擦系数，分别是转子支承限位器系统的在不同碰摩参数下的演变行为。在摩擦系数为0.5时，转子运行轨迹最终趋于中心处，且不发生碰摩，这个是无碰摩的稳定解。在摩擦系数为0.6时，转子在冲出间隙后稳定运行在约5倍的间隙处，以非常缓慢的速度发散，这属于全周碰摩解。在摩擦系数为0.8时，转子冲出间隙后直接以“螺旋形”发散，这属于失稳解。碰摩刚度1×106N/m时的轴心轨迹如图3(d)－图3(e)所示，共有0.1，0.2两个摩擦系数的计算结果，分别是无碰摩的稳定解和失稳解。和碰摩刚度1×103N/m时相比，并没有全周碰摩，说明随着碰摩刚度增大全周碰摩解会消失。

在试验中观察到了无碰摩的稳定解，如图4中（a）所示，同样观察到了“全周碰摩”的轴心轨迹，如图4中（b）所示。在试验中，由于限位器存在，转子振幅不可能无穷大，因此计算的失稳解在实际中的轴心轨迹近似“全周碰摩”时的情况，如图4中（b）所示。

3 碰摩发展过程

将不同碰摩刚度和摩擦系数下转子支承限位器系统受简谐激励时的碰摩演变过程中振动信号的频域信息提取出来，如表1所示。

将此碰摩演变过程按时间分为：“稳定”，“冲击”，“全周碰摩”和“恢复”4个阶段，分析不同时间阶段的主频，并与试验结果对比。

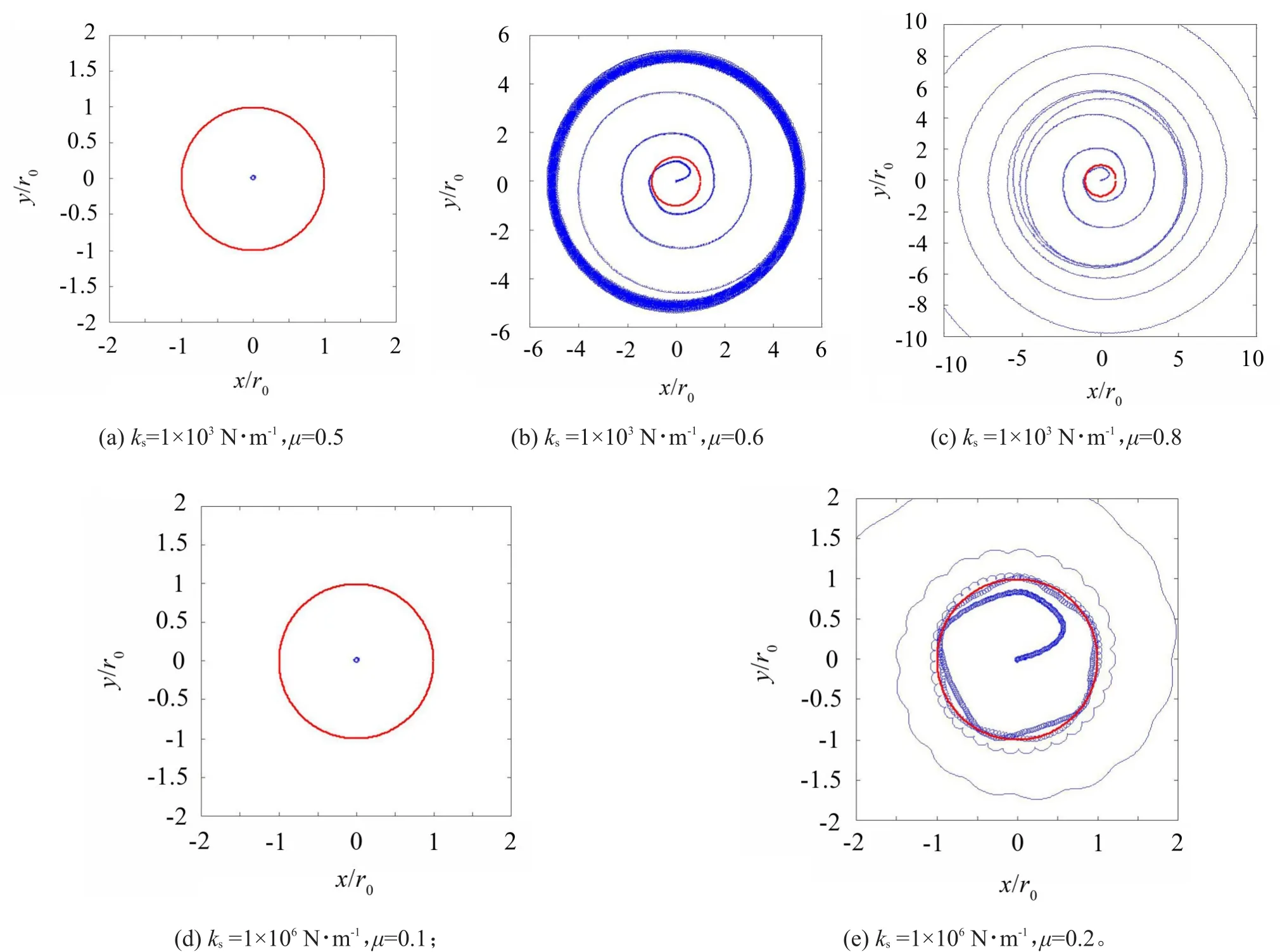
图3 不同碰摩参数下转子支承限位器系统的轴心轨迹

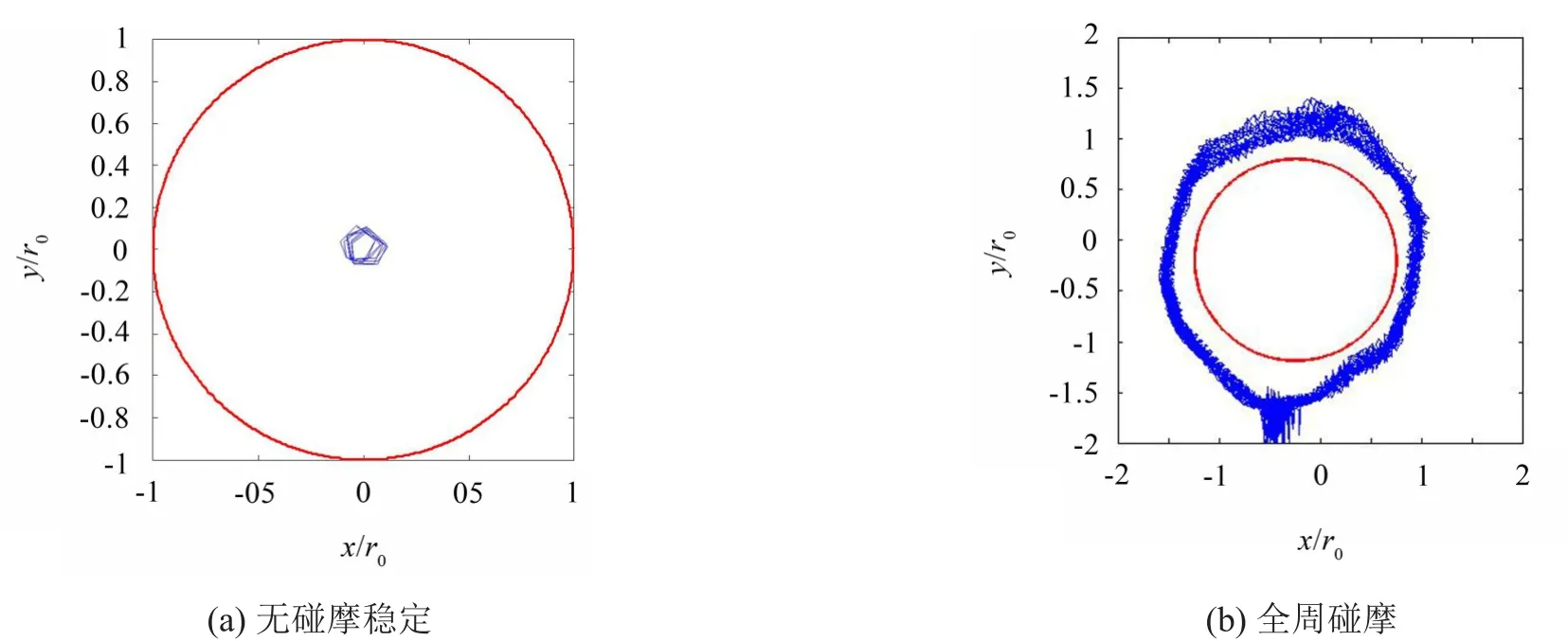
图4 试验中转子支承限位器系统的轴心轨迹

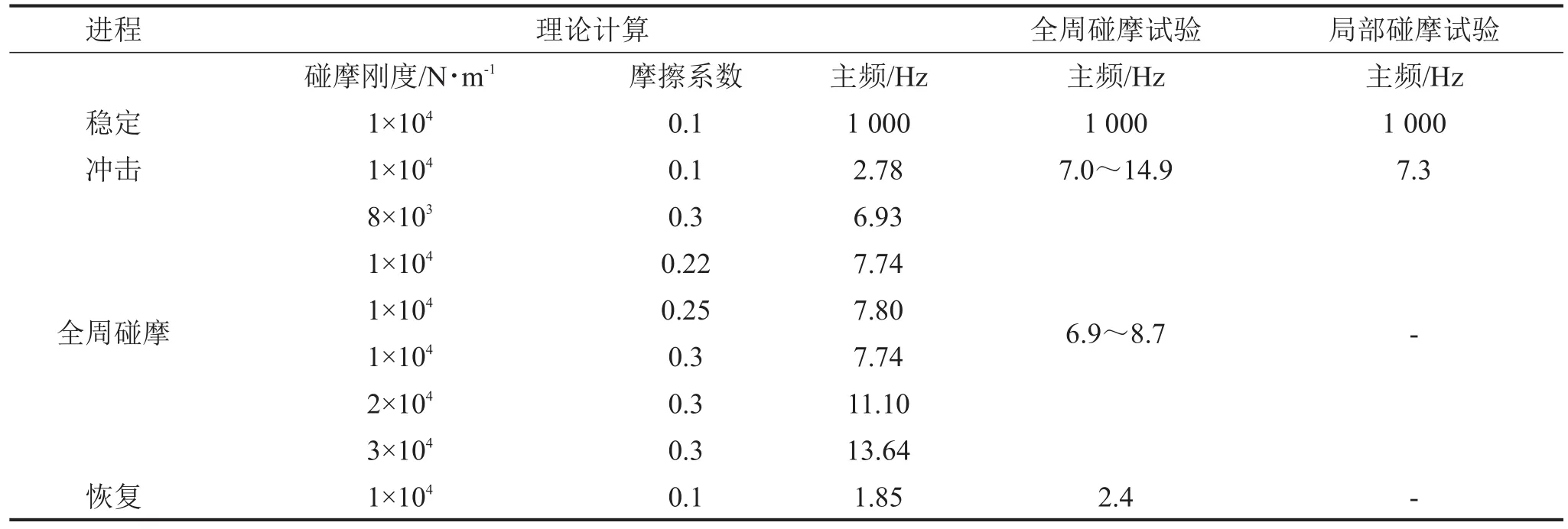
表1 碰摩过程中的频域信息

在“稳定”阶段时，表中碰摩刚度和摩擦系数下的主频为1 000 Hz，与试验中稳定运行时的主频相同，这是因为在没有外部干扰时的系统主频必然是转速频率。在“冲击”阶段，计算的主频为2.78 Hz，全周碰摩试验中的主频分布在7.0 Hz～14.9 Hz，局部碰摩中为7.3 Hz。一般而言，在冲击时引起的进动信号应该更接近系统的1阶频率即2.78 Hz，但试验中的主频分布却和全周碰摩时的接近，说明碰摩时转子和限位器接触时的摩擦对转子振动信号产生了很大影响，假设碰摩时只有碰撞没有摩擦，则冲击时的主频必然在系统1阶频率附近，引入摩擦后系统1阶主频发生变化。在“全周碰摩”阶段，计算了一系列碰摩刚度和摩擦系数下的主频，大小从6.93 Hz～13.64 Hz。试验中“全周碰摩”时的频谱如图5所示。其主频在6.9 Hz～8.7 Hz，说明转子和限位器之间的碰摩刚度约为1×104N/m。试验中“冲击”时的频谱如图6所示。其最大主频约为14.9 Hz，和碰摩刚度为3×104N/m时计算的主频接近，说明“冲击”时的实际碰摩刚度约为3×104N/m。从计算结果来看，全周碰摩时的主频主要和碰摩刚度有关。

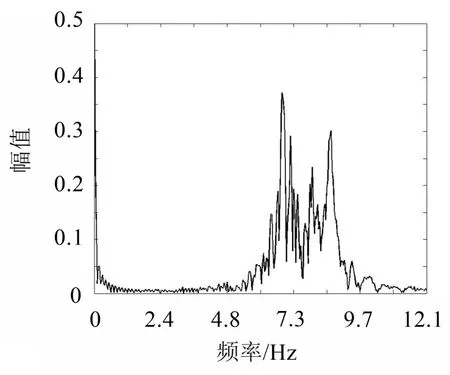
图5 全周碰摩时转子振动频谱图

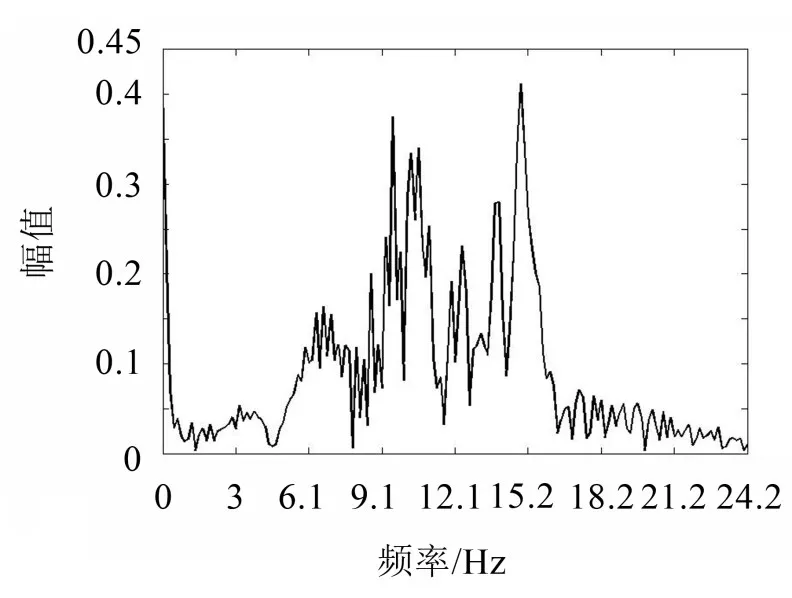
图6 冲击时的转子振动频谱图

4 结语

（1）包含限位器的高速旋转柔性支承转子系统在不同碰摩参数下有三种可能的碰摩行为：无碰摩稳定、全周碰摩和失稳。

（2）外来激励下系统响应的频域信息表明，在碰摩冲击和发生全周碰摩时的主要频率和碰摩刚度有关系。

（3）根据不失稳时的碰摩参数可以设计出保证系统不发生动力学失稳的限位器。