基于凝聚度和紧密度的网络节点重要性排序

张惠玲

（西安航空学院理学院 西安 710077）

1 引言

随着信息技术的迅猛发展，人类进入了网络时代，各种网络在结构、节点等方面具有一定的复杂性，在现实生活中受到各种因素的影响，因此它们也被称为复杂网络。作为复杂网络的一个研究热点，重要节点的排序引起了人们的极大关注。所谓重要节点指的是相对于网络中的其他节点，能够在更大程度上影响网络的结构与功能的一些特殊节点［1］。

人们一般从网络的局部属性、全局属性、网络位置以及随机游走等四个角度出发来分析网络节点的重要性，从而给出了一系列的评价指标［2］。基于局部属性的节点重要性排序指标主要考虑节点的自身信息和其相邻节点的信息，如节点的度。在文献［3］中，王建伟等认为节点的度及其相邻节点的度与节点的重要性呈正相关。在文献［4］，任卓明等考虑了相邻节点的个数以及相邻节点之间的紧密程度，给出了一种新的评价方法。在文献［5］中，定义最重要的节点是该节点在失效的情况下，相应地生成树数目最小的节点记为最重要节点。在文献［6］中，通过最短路径结束的方法确定网络中的重要性节点。文献［7］利用节点收缩的方法，通过删除待分析节点的邻接点来判断节点的重要度，该方法简化了计算的复杂度，但没有考虑节点删除后会导致网络结构变化，从而引起节点重要性的变化。文献［8］提出了基于网络性能梯度的节点重要性评价方法。在文献［9］中，将节点的度平均分配到各个相邻节点后，又结合介数构造了重要度评价矩阵，由此给出了节点重要度评价方法。针对文献［9］中节点度平均分配的不足，文献［10］对其进行了改进，构造了一种新的评价矩阵，优化了评价方法。文献［11］～［13］分别从不同的角度构建了网络节点的重要性评价指标评价，然后使用SIR模型做了验证，并且验证了方法的有效性。

基于全局属性的指标主要考虑全局的信息，这些指标一般准确性较高，如在文献［11］中，在万有引力公式的启发下，考虑节点的度和距离构建了节点重要度评价指标。在文献［12］中，提出一种基于距离的染色方法来判断网络节点的重要性。文献［13］中，考虑边权重，对K-shell指标做了改进，构建了一种新的指标确定节点的重要性。文献［14］中，通过定义限制度效率和等级度效率，构建节点的重要性评价矩阵，从而判断通信网中节点的重要性。文献［15］中，从网络的备选路由数、网络被分割的程度和网络性能三方面考虑了节点的重要性。

紧密度考虑了节点与其它节点之间的最短距离的平均值，发现距离越大，该节点对其他节点的影响力越低，于是将紧密度定义为平均距离的倒数，表明节点的紧密度越大，该节点越重要。在本文中，我们首先定义了网络节点的凝聚度，是一种新的刻画网络局部属性的节点重要性排序指标，而网络节点的紧密度是一种基于网络全局属性的节点重要性排序指标，然后将两个指标结合起来定义了网络节点的重要度指标，给出了相应的算法及其复杂性，最后通过实验分析验证了该方法的有效性。

2 评估模型

设图G=(V,E)由n个节点m条边组成的无向网络，di表示节点vi的度，N(vi)表示与节点vi相邻的点的集合，dij表示节点vi为起点，vj为终点的最短路径。G的邻接矩阵 M=(mij)n×m，其中

定义1［2］节点紧密度定义如下：

用来衡量网络中节点vi对其他节点的影响力，根据定义1，节点的紧密度C(i)越大，表明该节点越居于网络的中心，该节点在全局网络中越重要。

对该指标归一化，有：

定义2节点凝聚度

由于与节点距离为1的相邻节点提供的信息最多，因此提出了节点vi的凝聚度，即节点vi及其相邻节点所有节点对之间最短路径的平均值。定义如下：i

定义3节点的重要度

称

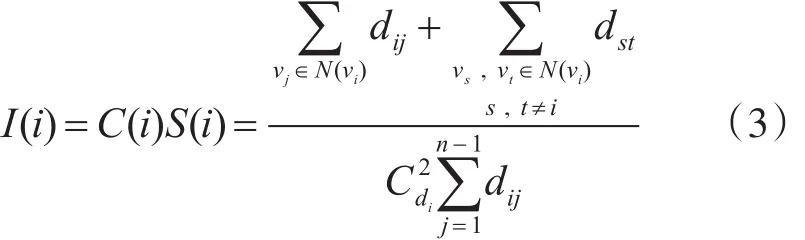
为节点vi的重要度。

3 算法及其复杂性

下面给出节点重要性评估算法步骤：

输入：邻接矩阵 M=(mij)n×m。

输出：节点vi的重要度。

步骤1根据Dijkstra算法计算所有节点对之间的最短距离；

步骤2根据式（2）计算所有节点的凝聚度；

步骤3根据式（3）计算所有节点的重要度。

该算法的复杂性取决于所有节点对之间的最短距离的计算，而Dijkstra算法的复杂性为o(n2)，故该算法的复杂性为 o(n2)。

4 实例分析

下面利用图1 ARPA网络拓扑的节点重要性评价算法进行分析。它由21个节点和23条边组成，大部分节点的度为2。

图1 ARPA网络拓扑

如果采用文献［7］中的节点删除法，删除节点v3,v4,v7,v8后，生成树的数目为0，于是相应的节点重要度是1。但从直观上判断，v3,v8与 v4,v7的重要度是有区别的。采用本文提出的方法计算，由表1的计算结果知v4,v7的重要度要高于v3,v8。

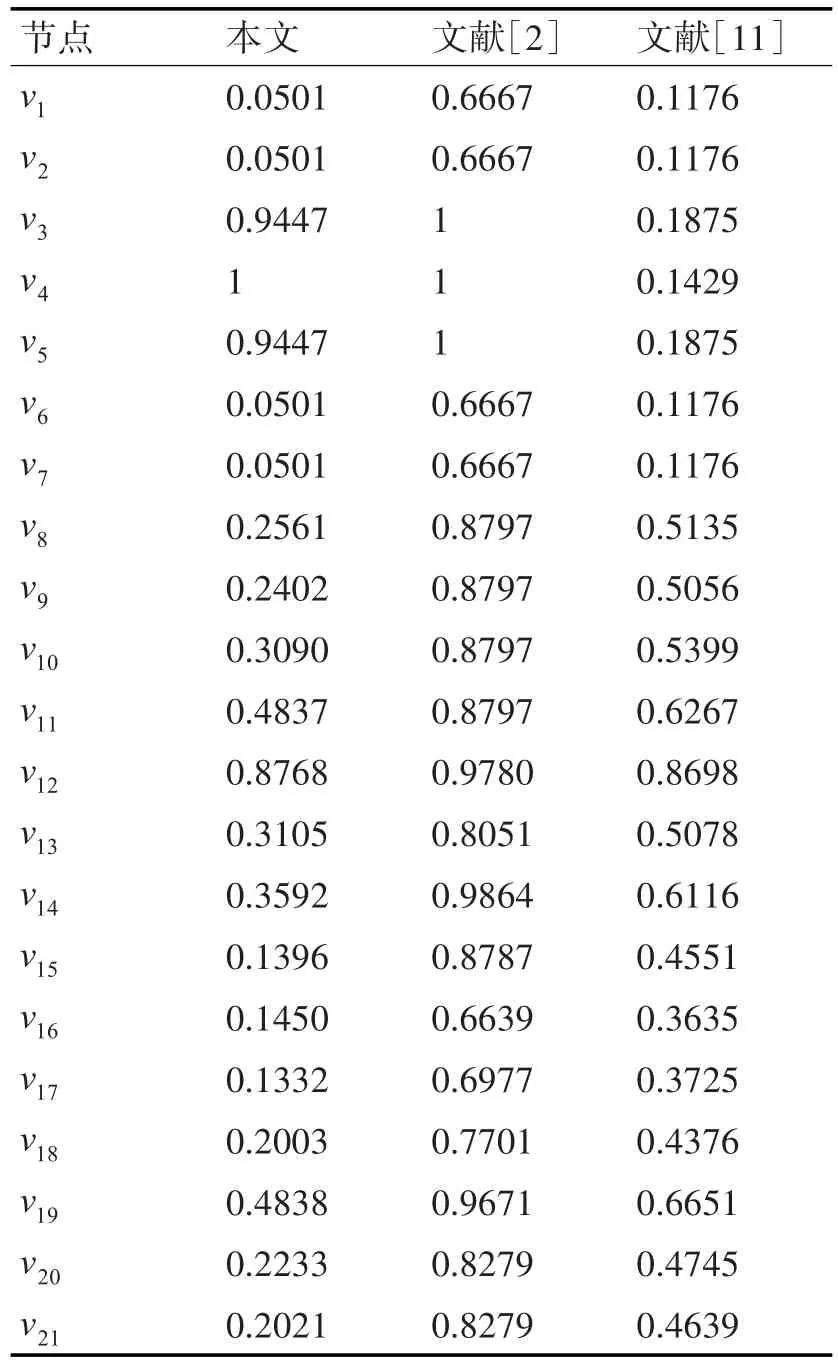
表1 节点重要性排序

5 结语

评估网络节点的重要性一直是复杂网络中的一个热点，本文首先定义了节点的凝聚度，然后将节点的紧密度归一化，定义了节点的重要度指标，该指标既考虑了节点的全局属性，又考虑了局部属性，有效地克服了单一指标判断节点重要性的弊端，对于有效评价网络节点的可靠性和重要性，有着十分广泛的实际意义。