电气化铁路动态弓网接触电阻研究
刘方林
(国家知识产权局专利局专利审查协作四川中心,成都 610200)
电气化铁路具有资源节约、环境友好、运量大等特点,在世界范围内具有广泛的应用。电力机车的电能来自于架设在铁路沿线的牵引网系统,通过安装在列车顶部的受电弓实现电能的传输。然而,与传统电力系统不同,接触网和受电弓之间属于滑动接触,容易造成电能传输的不稳定[1]。一方面,表现在弓网系统的动力学性能,弓网之间的剧烈振动会引起接触质量的下降[2],严重的还会导致离线的发生,危害运行安全[3];另一方面则表现在弓网之间的电接触特性,弓网之间的滑动接触电阻受诸多因素决定,影响着弓网间的电能传输质量[4]。以下分别对二者以往的研究进行综述。
在弓网动力学性能研究方面,文献[5]基于有限元方法构建了电气化铁路接触网静态模型,可进一步用于动力学特性的研究。文献[6]同时建立了多种受电弓模型,研究了受电弓划过接触网时的动力学特性。文献[7]通过引入受电弓模型,分析了强风对弓网动态特性的影响。文献[8]提出了受电弓控制策略,用于改善弓网间的电能传输质量。
在弓网电接触方面,众多学者开始关注受电弓与接触网之间的接触电阻。文献[9]考虑触头的静态接触电阻特性,提出了膜触头的接触电阻数值计算模型。文献[10]研究了收缩电阻的动态特性,对收缩电阻的有效区域范围进行了进一步的划分,分析了电镀层等因素对收缩电阻的影响,并提出了考虑镀层影响的导体间接触电阻的数值模型。针对弓网这一特定系统的接触电阻,文献[11]采用曲线拟合的方法得出了弓网接触电阻与电流、车速和接触力的对应关系。文献[12]针对滑动接触特性,采用弓网电接触试验台分析了接触电阻对接触力、电流、车速的关联。
然而,在以往的研究中,弓网的动力学研究和电接触研究是分开进行的。但实际上,动力学仿真计算中的接触力是影响弓网接触电阻的直接因素,在稳定运行中,弓网间的接触状态受接触电阻的影响。因此,本文针对以往研究的不足,研究接触电阻的动态特性。首先,根据以往的研究结果,分析弓网接触电阻的影响因素;其次,通过弓网动力学仿真得到弓网间的动态接触压力;最后,建立动力学计算和电接触计算的关联性,分析接触电阻随弓网接触力的波动特性。
1 弓网接触电阻模型
以往研究认为弓网接触电阻的影响因素主要有电流和接触力,文献[11]提出弓网静态电接触时接触电阻的计算式为

式中,cR为接触电阻,f为接触力。b、n、d分别为与电流有关的参数。通过最小二乘法优化理论计算与试验的误差,可以得到的接触电阻的解析表达式为

式中,I为受电弓滑板和接触线接触点的电流的有效值。然而,式(2)并未考虑弓网滑动接触效应,通过引入车速,滑动接触电阻的计算公式可修正为[12]
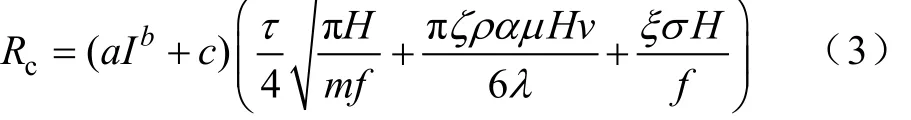
式中,a、b、c为经验拟合参数;τ为弓头滑板和接触线的电阻率之和;H为滑板的材料硬度;m为导电斑数;σ为材料的电阻率;ζ和ξ分别为电阻相关的修正系数;λ为材料热导率。与以往不同的是车速v也被引入到接触电阻计算中。本文采用该模型分析接触电阻的特性。
2 静态接触电阻分析
本小节分析不同车速、电流和接触力下弓网静态接触电阻的变化规律。图1给出了v=350km/h时接触电阻随电流和接触力的变化图。可以看出,接触电阻随着接触力和电流的减小而增大,接触电阻对电流的变化更加敏感,当电流为0时,接触电阻上升明显。图2给出了I=200A时,接触电阻随车速和接触力变化图,可以看出,车速的增加和接触力的减小都会导致接触电阻的增大。图3给出了当f =100N时,接触电阻对车速和电流的变化图,可以看出,车速的增大和电流的减小都会导致接触电阻的增加,电流较小时,接触电阻对电流变化十分敏感。
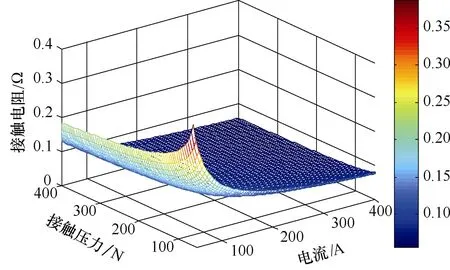
图1 车速350km/h时不同接触力和电流下接触电阻

图2 电流200A时不同车速和接触力下接触电阻

图3 接触力100N时不同车速和电流下接触电阻
3 动态接触电阻分析
以上研究主要分析了接触电阻的影响因素,但是所计算出的接触电阻是在接触力一定的前提下。弓网实际运行时,弓网间接触力的波动是十分剧烈的,接触电阻也是一段时变的时间历程。因此,本节首先建立弓网的动力学仿真模型,得到弓网间的接触力,然后分析不同车速下的动态接触电阻。
接触网结构如图4所示,采用张力梁单元描述接触线和承力索的垂向运动,其运动微分方程为

式中,(,)yxt为接触线或承力索的垂向位移;Aρ为线密度;EI为未分段抗弯刚度;(,)fxt为接触力;T为接触线或承力索的张力;C为线索阻尼。采用分离变量法,式(4)可展开为以下形式:
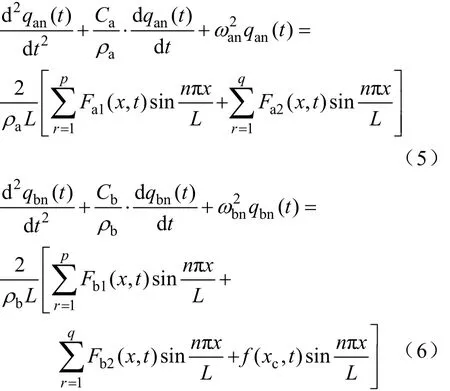
式中,qan(t)和qbn(t) 分别为承力索和接触线广义位移;xc为弓头为接触线上的接触点位置;Fa1(x,t)和Fa2(x,t)分别为吊弦和支撑杆对承力索的贡献,Fb1(x,t)和Fb2(x,t)分别为吊弦和定位器对接触线的贡献,p为吊弦的个数,q支撑杆和定位器的个数,n为模态阶数,L为锚段长度,ωan和ωbn分别为承力索和接触线的自振角频率。
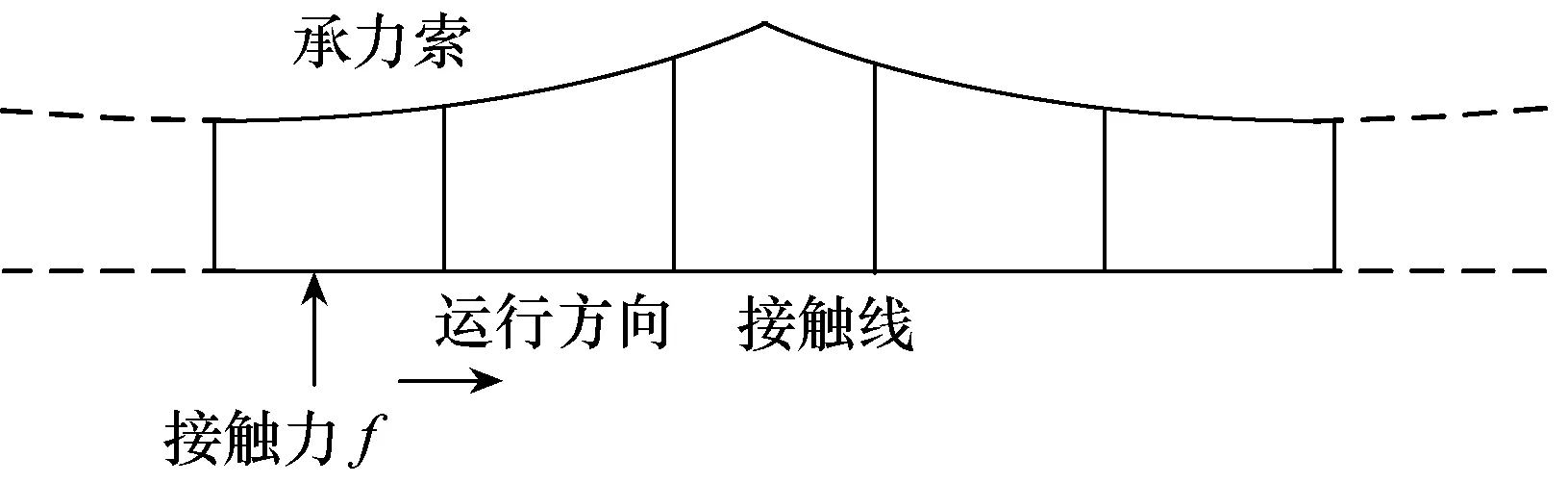
图4 接触网模型示意图
受电弓采用三元归算质量模型,弓网相互作用可采用罚函数来表示,具体参见下式:

式中,Ks为接触刚度;y1为弓头位移;yb为接触线位移。结合式(5)和受电弓归算质量模型,可建立弓网动态交互模型,实现实际工况下弓网的动态仿真。
结合我国高速铁路实际弓网参数,仿真工况设为:v=250km/h和v=350km/h。在3个速度等级下的弓网接触力如图5所示。可以看出,弓网接触力是一段波动较为剧烈的时间历程,随着车速的提升,接触力的波动也相应提升。

图5 不同速度下的弓网接触力

图6 v=250km/h时不同电流下的弓网动态接触电阻
将图5得到的接触力时程引入弓网接触电阻模型,可以计算得到不同工况下的弓网接触电阻变化时程。当弓网间电流为70A和110A时,且v= 250km/h时的弓网动态接触电阻的变化图如图6所示。可以看出,相同速度时,弓网接触电阻随时间变化的波形是一致的,但是其极值和均值会受到电流有效值的影响。表1给出了不同电流和车速下的接触电阻统计量,可以看出,当车速一定时,接触电阻的统计量都随电流的增加而减小,当电流大小一定时,接触电阻的统计量都随车速的增加而增大。车速的增加不但能够增加弓网系统的机械振动,同时也会增大弓网间的接触电阻。因此,弓网受流质量会随车速的增大而增大,无论从电气还是动力学角度,都可以解释该结论。

表1 不同车速和电流下弓网接触电阻统计量
4 结论
本文基于高速铁路受电弓和接触网相互接触时的滑动接触电阻模型,分析了接触电阻大小的影响因素。为了弓网滑动引起的动态效应,采用动力学理论构建了弓网动力学模型,得到弓网高速滑动时的动态接触压力,将其带入弓网接触电阻模型,得到动态接触电阻的变化趋势。通过分析不同车速、电流下的弓网接触电阻随时间的动态变化曲线和统计值,其结论表明,接触电阻随车速的增加而增大。车速的增加不但能够增加弓网系统的机械振动,同时还会增大弓网间的接触电阻。弓网受流质量的恶化机理无论从电气还是动力学角度都得到了合理的解释。
本文所得到的动态接触电阻可用于进一步分析弓网的电能传输效率。在弓网结构优化中,也可将传统的接触力优化目标细化为具体的车网电气参数。

