基于表观压缩实验与有限元分析相结合的骨微观力学性能参数预测方法的研究*

范若寻，刘杰，甘树坤，张敏

(1.吉林化工学院汽车工程学院，吉林 132102；2. 吉林大学机械科学与工程学院，长春 130025)

1 引 言

随着医疗技术的发展，骨性能测试变得简单可行，其中骨表观力学参数常被用来评判人体骨质量及预测骨折风险[1-2]。但由于骨结构分层水平特性，其表观力学性能往往由不同水平骨材料性能所决定[3-5]。因此，骨微观力学性能对表观性能，甚至是骨质量与骨折风险均有影响，尤其是骨在微观水平的失效参数，对骨在不同水平力学性能有直接影响：在表观水平，骨微观失效应变在一定程度上决定了骨结构强度极限；在组织水平，骨微观失效应变则影响着松质骨小梁的损伤与重建过程[2,6-9]。因此，为深入了解骨疾病的发病机理，以及预测人体骨质量与骨折风险，除了掌握表观力学性能，更需对骨的微观力学性能参数进行预测与研究。

有限元分析被认为是解决生物医学工程，特别是骨力学问题的一种有效方法[2-3,9]。然而，有限元模型材料参数的选取却是一个影响分析精度的重要问题[6,10-11]。一些仿真参数，如弹性模量，随着纳米压痕等实验技术的发展，已能准确测得[2,8]。而当对骨结构进行断裂模拟时，需输入骨在微观水平的材料参数，例如骨组织屈服与断裂应变等，由于这类参数难以通过实验测得，所以针对骨结构的断裂仿真模拟，一般是依据文献或经验公式赋予微观水平材料参数，这在一定程度上降低了有限元模型的生物逼真度与分析准确性[3-4,9]。

既然骨在微观水平的力学性能参数对临床医学及有限元分析均有重要意义，如何测得该水平上的力学参数即成为一个重要问题。因此，本研究的目的为开发一种骨微观力学性能参数预测方法，以大鼠股骨皮质骨为研究对象，以表观压缩实验数据为研究依据，通过结合实验与有限元仿真技术，预测骨的一种微观力学性能参数——微观失效应变。

2 材料与方法

2.1 表观压缩实验

选取四只7月龄雄性大鼠，获取其右侧股骨，在股骨中部截取5 mm长皮质骨，作为实验样本，置于试验机中进行压缩实验，压头压缩速度以位移量控制。将皮质骨上表面与压头下表面的接触面积作为计算表观强度极限的横截面积，四个样本的横截面积范围处在26～29 mm2，依据样本的力-位移曲线计算其表观应力-应变曲线。

2.2 皮质骨有限元模型建立

基于大鼠皮质骨微观影像，利用逆向建模软件重构皮质骨外表面，通过有限元软件应用三维四面体单元建立皮质骨有限元模型，最后在皮质骨模型上、下方分别加入刚性压板，其中下压板作为固定端，约束所有自由度，同时将0.5 mm的压缩位移施加在上压板，以模拟实验条件，见图1。由于网格的疏密程度对有限元仿真结果有较大影响，所以针对同一样本分别建立了网格尺寸为5、10、15、20、25、30、35、40 μm的有限元模型，进行网格敏感性分析，以确定网格尺寸。大鼠股骨皮质骨的弹性模量由课题组前期所做纳米压痕实验测得，7月龄大鼠股骨皮质骨的弹性模量平均值为34 000 MPa，泊松比为0.3[2]。

图1 大鼠股骨皮质骨有限元模型示意图

Fig1Schematicdrawingoftheratfemoralcorticalbonefiniteelementmodel

2.3 骨微观力学性能参数预测方法

大鼠股骨皮质骨有限元模型的断裂由内部等效应变控制[6-7]。这里采用单元删除技术：当单元达到失效条件时，即等效应变超过皮质骨材料的微观失效应变时，该单元即视为被删除，将被删除单元的弹性模量设定为1 MPa[2,4]。随着压缩载荷持续增加，越来越多的单元被删除，当被删除单元达到一定数量时，有限元模型即会发生表观断裂失效。

为模拟上述过程，本研究在有限元软件中编写了子程序USDFLD，将上述分析思路与单元失效判定条件写入子程序。由于其它仿真输入参数均为已知，仅有微观失效应变这一未知输入参数。因此，只需在子程序中尝试赋予微观失效应变数值即可模拟出皮质骨在压缩载荷作用下的断裂。将仿真得到的表观应力-应变曲线与样本压缩实验测得的应力-应变曲线相对比，观测二者拟合情况，如拟合不成功，则需调节预设微观失效应变，直至曲线拟合成功(拟合成功的标准为仿真与实验测出的表观断裂应变差值小于5%)，即认定此时预设的微观失效应变为拟获取的大鼠股骨皮质骨微观失效应变，具体仿真流程见图2。

3 结果

图3显示了同一样本采用不同网格所建立的有限元模型在压缩载荷作用下得到的表观断裂应变。可以看出，最大与最小网格尺寸模型所得到的数值差异达到了25.977%，同时表观断裂应变随着网格尺寸增大显著减小，但当网格尺寸小于20 μm 时，不同有限元模型得到的表观断裂应变数值差异却都小于5%。因此，考虑到仿真准确性与计算成本，大鼠股骨皮质骨有限元模型的网格尺寸均选取为20 μm。

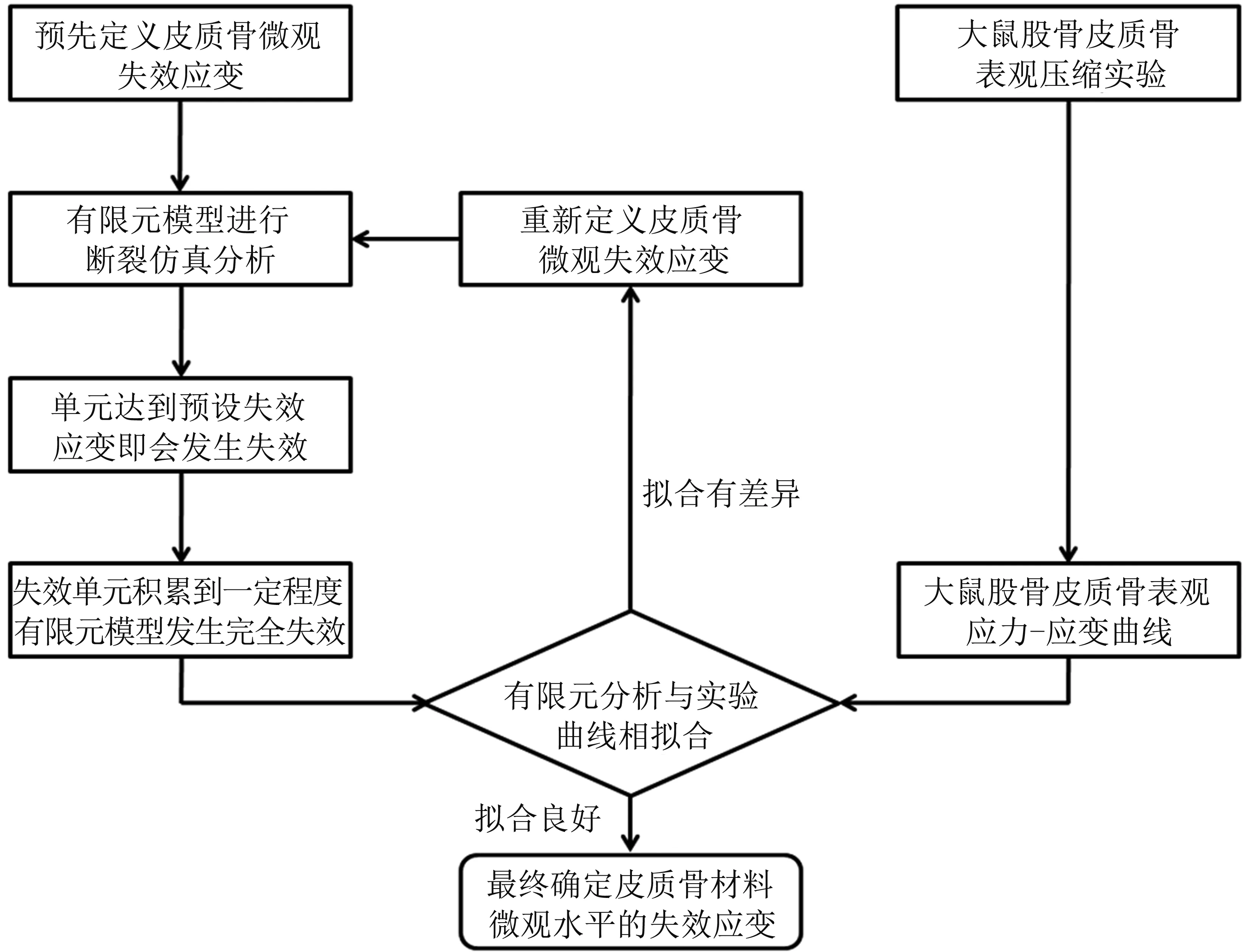
图2大鼠股骨皮质骨微观失效应变预测流程

Fig2Simulatedprocessonthemicro-levelfailurestrainofratfemoralcorticalbone

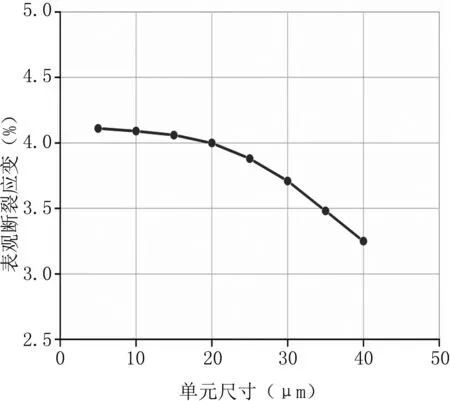
图3 单元尺寸对表观断裂应变的敏感性分析

Fig3Meshsensitivityanalysisfortheeffectofelementsizesontheapparentfailurestrain

通过与表观压缩实验数据进行反演分析，反复调节预设微观失效应变，四个皮质骨模型均成功拟合出实验测得的表观应力-应变曲线，其中预测出的微观失效应变以及模型发生表观断裂时失效单元数量所占百分比见表1。可以看出，同一月龄的大鼠股骨皮质骨的微观失效应变数值差异较小，而且当失效单元数量占所有单元比例达到6%～7%时，皮质骨有限元模型即可能发生表观断裂失效。

表1大鼠股骨皮质骨的微观失效应变数值与失效单元百分比

Table1Thepredictedmicro-levelfailurestrainsforratfemoralcorticalbonesandthefailedelementpercentage

样本微观失效应变(%)失效单元百分比(%)样本14.626.35样本24.536.21样本34.656.43样本44.757.22

图4显示了四个大鼠股骨皮质骨样本通过有限元分析与表观压缩实验获得的表观应力-应变曲线对比。可以看出仿真所得的曲线形状与实验较为吻合，同时仿真预测出的表观强度极限和断裂应变数值也与实验结果相差无几，差异均保持在5%以内。

4 讨论

本研究通过采用一种将表观压缩实验与有限元仿真相结合的方法，预测出大鼠股骨皮质骨的一种微观力学性能参数。长期以来，骨裂与骨折等骨科疾病一直困扰着人们，特别是老年人，一旦发生骨折将导致一系列严重后果[5,11]。然而研究表明，骨折的发生除了外力作用，并非仅与骨密度的降低或骨结构的退变等表观因素相关，在很大程度上也取决于微观力学性能的退变[3,12]。因此，研究骨微观力学性能参数的预测方法，对骨疾病的诊断与预防都将起到重要作用。

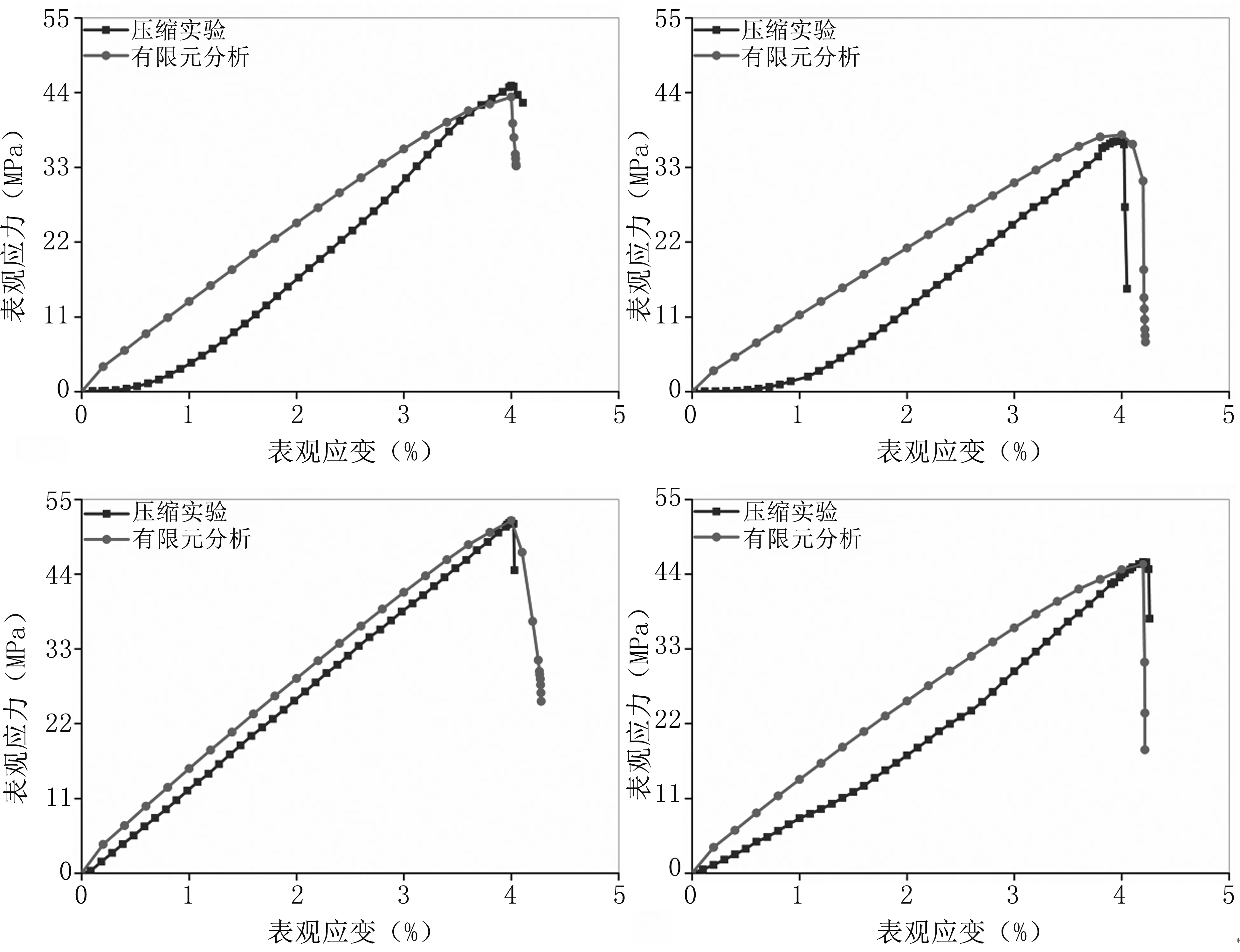
图4四个皮质骨样本有限元分析与压缩实验获得的表观应力-应变曲线对比

Fig4Comparisonoftheapparentstress-straincurvesbetweenfiniteelementanalysisandcompressiveexperimentforfourcorticalbonesamples

骨微观力学性能参数的测试一般需借助不同水平的实验手段完成[1]。相比表观实验，微观实验不但操作复杂，而且对样本精度也有较高要求，所以，针对微观力学性能参数的测试长期以来都是一个难点[6,13]。基于此，本研究通过结合表观压缩实验与有限元仿真技术，开发了一种骨微观力学性能参数预测方法。该方法不但避免了难度较大的微观实验，而且通过与实验应力-应变曲线对比发现仿真得出的皮质骨表观断裂应变数值与实验数值差异均小于5%，同时通过观察发现皮质骨样本与皮质骨有限元模型在压缩载荷作用下的断裂模式也较为相似，这些均说明了本研究所开发预测方法的可行性以及获取皮质骨微观失效应变参数的准确性。因此，本预测过程为骨微观力学性能参数的获取提供一定帮助。同时，该方法不仅可以预测微观失效应变，也可结合相关表观实验预测其它微观力学性能参数，例如骨材料的弹性模量或松质骨的微观屈服应变等微观力学性能参数。

断裂模拟过程中，为保证仿真分析精度，首先要设置足够小的载荷增量步，以保证当预设微观失效应变有微小调整时，仿真得出的应力-应变曲线会有相应变化；同时在与实验曲线进行反演分析时发现，当对预设微观失效应变进行调节时，相比表观断裂应变，仿真得出的表观强度极限的变化幅度更大，即当对预设值进行微小调整时，表观断裂应变的预测值不会有太大波动，但表观强度极限的变化却较大。结合该特点，在模拟过程中，首先确保表观强度极限的预测值与实验结果相符，以大致确定预设微观失效应变的范围，然后在此范围内小幅度调整，以找到与实验所测数值最为吻合的预设失效应变。

本研究在断裂模拟过程中应用了单元删除技术，该技术能够模拟出单元从开始变形至最后失效的力学性能变化过程，但无法表达出单元的屈服过程，因此，该技术目前更适用于模拟材料的脆性断裂。依据实验结果显示，大鼠皮质骨呈现出脆性断裂特征，所以应用单元删除技术能够准确模拟出皮质骨模型的断裂过程。而人体松质骨会表现出韧性断裂特征，因此为了预测松质骨的微观力学参数，日后准备基于ABAQUS平台，通过开发UMAT子程序，应用连续损伤技术，以模拟松质骨单元的屈服与断裂过程，从而对松质骨与皮质骨结构进行全面的断裂模拟。

5 结论

本研究提出了一种骨微观力学性能参数预测方法，以表观压缩实验为研究依据，通过模仿实验条件，应用USDFLD子程序模拟出大鼠股骨皮质骨有限元模型在压缩载荷作用下的断裂过程，并通过与实验所测数据进行对比、反演，预测出大鼠股骨皮质骨的微观失效应变。结果表明四只7月龄大鼠，其股骨皮质骨的微观失效应变数值处于4.53%～4.75%之间。经实验对比验证显示，该方法能够准确预测出骨结构在微观水平的力学性能参数。