基于局部联合熵梯度的双向多分辨率Demons算法*

王昌，任琼琼，秦鑫，刘艳，张文超，于毅

(新乡医学院 生物医学工程学院, 河南 新乡 453003)

1 引 言

近年来，医学图像配准已广泛应用到病变组织的分割、信息融合和病变检出。Hellier等对常用的配准算法进行分析比较，证明demons算法优于其他配准算法[1]。许多学者针对异体配准中由个体差异及占位性病变所导致的大形变问题进行了改进。2005年，Wang等人将浮动图像的梯度信息也引入驱动力计算公式中，提出了active demons算法[2]。2006年，Roglj提出了使用对称梯度形变力的symmetric demons算法[3]。2008年，林相波分析了两个分力的影响程度，提出扩展的active demons算法[4]。2007年，Vercauteren等人提出了additive demons算法，最终可根据实际配准的情况自动确定迭代次数[5]。2009年，为了保证变形场的拓扑保持性，提出了diffeomorphic demons配准算法[6]。2010年，徐峰等人引入正则项，创建新的能量函数，用以保证形变场的平滑性和可逆性[7]。

为解决大形变的配准问题，利用配准过程中图像的局部联合熵增加的规律，本研究引入了两幅图像局部联合熵参数，将图像局部联合熵的梯度作为附加的demons驱动力，实现了基于局部联合熵梯度的双向多分辨率demons算法。利用均方误差、归一化互信息系数、结构相似度来评价配准结果,与active demons, diffeomorphic demons 进行对比分析，评测本算法的高效性。本算法可应用于大形变场医学图像的配准，具有一定的临床应用价值。

2 方法

2.1 Active demons算法

传统demons算法将配准过程看作是浮动图像向参考图像扩散的过程。设S和M为待配准图像，其中S是参考图像，M是浮动图像。S(x,y)为参考图像在(x，y)处的梯度，计算位移公式如下：

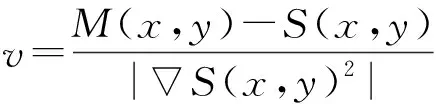
(1)

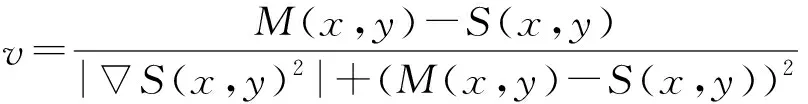
(2)

(3)

active demons算法根据作用力与反作用力的原理假设扩散是双向的，则驱动力修改为：

(4)

active demons容易受参数设置的影响，不能有效解决大形变场的配准问题。

2.2 基于联合局部熵的附加驱动力

对于大形变图像配准，仅依靠图像间的灰度差和灰度梯度完成形变配准是不准确的。当两幅图像的梯度特别小甚至趋于零时，图像形变的方向不能确定，无法保证形变场的拓扑保持性。本研究利用在配准过程中，图像的互信息不断增大，局部联合熵增加的规律[8]，引入了两幅图像局部联合熵参数，将图像局部联合熵的梯度作为附加的active demons驱动力，来保证形变场的拓扑性。确保在局部联合熵增大的方向上进行浮动图像与参考图像的配准，当局部联合熵达到最大时，两幅图像完成配准。

本研究将两幅图像局部联合熵的梯度作为附加力添加到active demons中，改进的驱动力如下式所示：

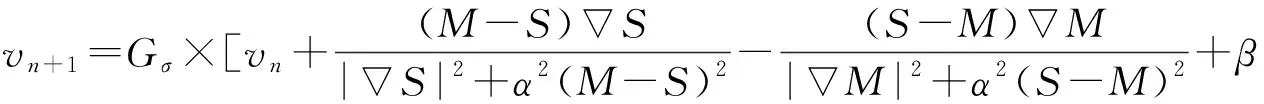
(5)

其中α、β为权重系数，MI是两幅图像局部联合熵的梯度。

图像A、B的局部联合熵定义为：

(6)

图像局部联合熵需要计算每个像素点的局部联合熵，像素局部联合熵的计算公式如下：

总之,胸、腹腔镜联合治疗食管癌患者术后并发症发生率较高,尤其以肺部感染发生率较高,加强外科基础护理并给予综合护理,能有效预防术后并发症的发生,提升患者术后生活质量。

(7)

利用公式(7)计算两幅图像局部联合熵，其实质是联合概率密度，在计算每个像素点的局部联合熵过程中，选择矩形区域大小为5×5。

2.3 算法实现

2.3.1算法流程 步骤1：对输入的参考图像和浮动图像进行降采样，形成多分辨率金字塔。初始化水平、垂直方向的偏移量。

步骤2：在低分辨率下，利用公式(5)计算其驱动力, 实现本研究提出的基于局部联合熵梯度的双向多分辨率demons算法。

步骤3：利用迭代的方法计算出粗略的偏移场。(低分辨率，迭代次数大；高分辨率，迭代次数小)

步骤4：对上一分辨率的偏移量进行重采样，作为下个分辨率下偏移量的初始值，返回步骤2。

在所有分辨率下完成配准，获得精确形变场。在此，利用形变场叠加原理更新形变场。

2.3.2配准的评价标准 用两幅图像的均方误差(mean square error, MSE)、归一互相关系数(normalized cross correlation, NCC)和结构相似性(SSIM)来评价配准算法。

均方误差的公式如下：

(8)

归一化互相关系数公式如下：

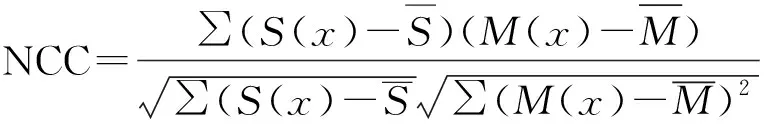
(9)

其中：S为参考图像，M为配准后的图像。

结构相似度，结构信息不受照明和图像对比度的影响，具体计算可参考文献[9]。

3 结果

将本研究提出的算法和多分辨率active demons, diffeomorphic demons进行实验对比，从而验证算法的有效性。本研究的参数主要有Gσ、α、β三个参数，Gσ为高斯滤波器，其中σ为高斯滤波器的参数，α、β为系数权重。在本实验中，参数选择如下：σ=2,α=1.0,β=1.0。

3.1 自然图像的对比分析

本研究算法和active demons, diffeomorphic demons对大形变的自然图像进行配准，其中图1(a)为参考图像，图1(b)为浮动图像，图1(c)为初始差值图像。

图1输入自然图像。(a)参考图像;(b)浮动图像;(c)初始差值

Fig1Inputnaturalimage. (a)fixedimage;(b)movingimage; (c)initialdifferencebetweenfixedandmovingimage

将本研究算法和active demons, diffeomorphic demons进行对比分析，图2是不同算法的配准结果，图3是不同算法得到的最终形变场，图4是配准结果与参考图像的差值图像，从图2～图4可以看出本研究算法的配准效果最好。

定量分析结果见表1，本研究的归一化互相关系数和结构相似度最高，均方误差最小。

图2自然图像配准结果对比。(a)本研究算法;(b)activedemons; (c)diffeomorphicdemons

Fig2Comparisonofregistrationresultfornaturalimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

图3自然图像形变场对比。(a)本研究算法;(b)activedemons; (c)diffeomorphicdemons

Fig3Comparisonofdeformationfieldfornaturalimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

图4配准结果与参考图像的差值图像对比。(a)本研究算法; (b)ActiveDemons；(c)diffeomorphicdemons

Fig4Comparisonofdifferencebetweenregistrationresultandfixedimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

表1配准算法的评价(自然图像)

Table1Evaluationofregistrationalgorithms(naturalimage)

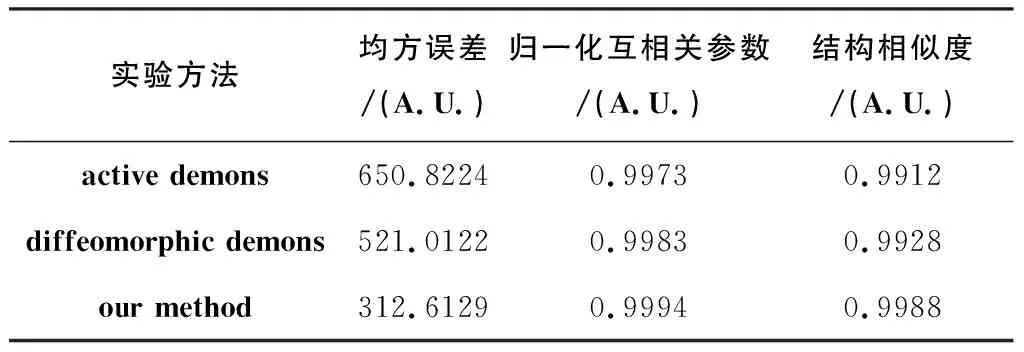
实验方法均方误差/(A.U.)归一化互相关参数/(A.U.)结构相似度/(A.U.)active demons650.82240.99730.9912diffeomorphic demons521.01220.99830.9928our method312.61290.99940.9988

3.2 MRI图像对比分析

选取磁共振T1图像(具有较大形变)进行配准，将相关算法进行对比，其中，图5(a)为参考图像，图5(b)为浮动图像图5(c)为初始的差值图像。

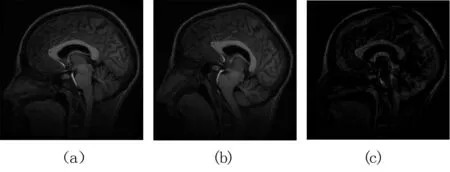
图5输入MRI图像。(a)参考图像;(b)浮动图像;(c)初始差值

Fig5InputMRIimage. (a)fixedimage;(b)movingimage; (c)initialdifferencebetweenfixedandmovingimage

将本研究算法和active demons, diffeomorphic demons进行对比分析，从图6～图7可以看出本研究算法的配准效果最好。定量分析结果见表2, 本研究的归一化互相关系数和结构相似度最高，均方误差最小。

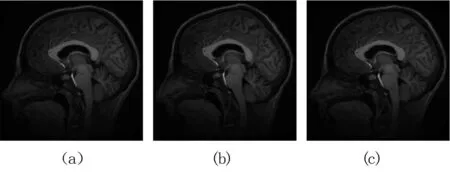
图6MRI图像配准结果对比。(a)本研究算法;(b)activedemons; (c)diffeomorphicdemons

Fig6ComparisonofregistrationresultforMRIimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

图7MRI图像形变场对比。(a)本研究算法;(b)activedemons; (c)diffeomorphicdemons

Fig7ComparisonofdeformationfieldforMRIimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

表2配准算法的评价(MRI图像)

Table2Evaluationofregistrationalgorithms(MRIimage)

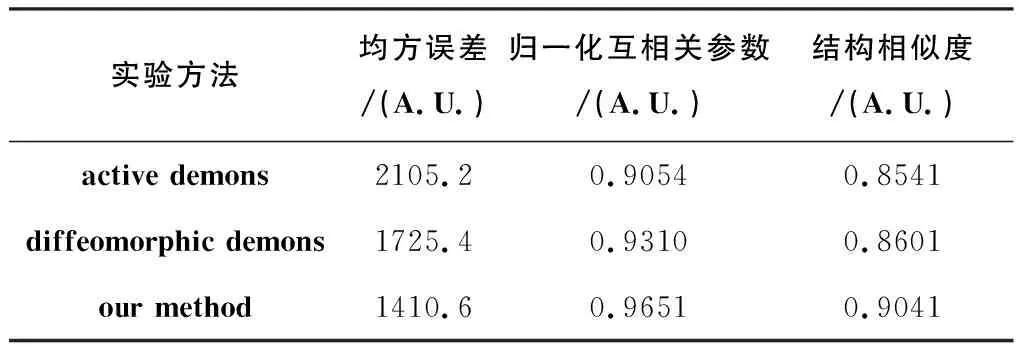
实验方法均方误差/(A.U.)归一化互相关参数/(A.U.)结构相似度/(A.U.)active demons2105.20.90540.8541diffeomorphic demons1725.40.93100.8601our method1410.60.96510.9041

3.3 CT图像的对比分析

将本算法应用于具有大形变的CT图像，选择医学图像为不同个体的同一层片，大小为512×512的高分辨率颅脑CT图像。配准对象是软组织区域，利用阈值法与形态学相结合的方法提取软组织区域。经过预处理后输入图像见图8,图8(a)为参考图像，图8(b)为浮动图像，图8(c)为初始的差值图像。两个图像之间存在大形变场。

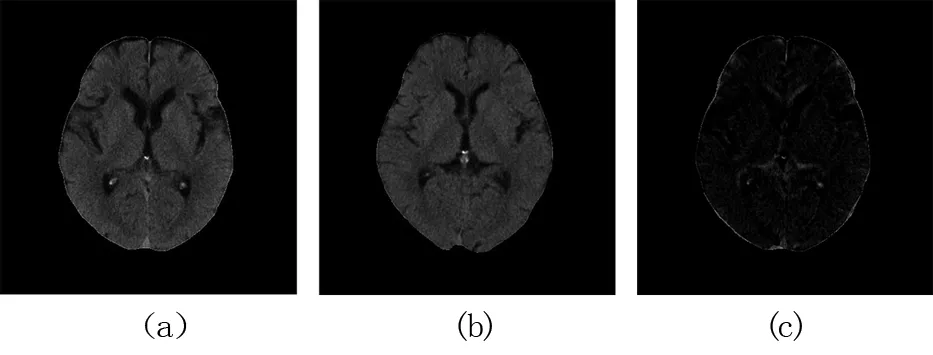
图8输入CT图像。(a)参考图像; (b)浮动图像;(c)初始差值

Fig8InputCTimage. (a)fixedimage; (b)movingimage; (c)initialdifferencebetweenfixedandmovingimage

将本研究算法和active demons, diffeomorphic demons进行对比分析，从图9～图10可以看出，本研究算法的配准效果最好。其统计结果见表3, 本研究的归一化互相关系数和结构相似度最高，均方误差最小。

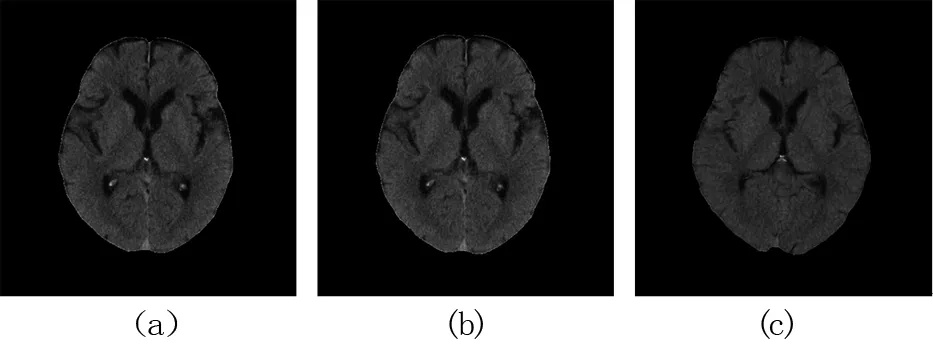
图9CT图像配准结果对比。(a)本研究算法;(b)activedemons; (c)diffeomorphicdemons

Fig9ComparisonofregistrationresultforCTimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

图10CT图像形变场对比。(a)本研究算法;(b)activedemons; (c)diffeomorphicdemons

Fig1ComparisonofdeformationfieldforCTimage. (a)ourmethod; (b)activedemons; (c)diffeomorphicdemons

表3配准算法的评价(CT图像)

Table3Evaluationofregistrationalgorithms(CTimage)

实验方法均方误差/(A.U.)归一化互信息参数/(A.U.)结构相似度/(A.U.)active demons1238.60.99810.9960diffeomorphic demons971.30.99020.9858our method819.30.99840.9978

3.4 参数对算法的影响

分析本研究算法中权重系数α、β对配准结果的影响,α=1.0。重点讨论β对实验结果的影响，处理的大形变图像是自然图像，通过改变权重系数β的大小来定量分析相关的配准指标。

从表4可以看出，β取1时配准的效果最好，获得的配准评价指标最佳。因此，在本研究中均采用α=1.0，β=1.0的参数设置进行配准。

表4权重系数β对配准结果的影响

Table4Influenceofweightcoefficientβonregistrationresults

权重系数(β)均方误差/(A.U.)归一化互相关参数/(A.U.)结构相似度/(A.U.)0.2508.43090.99840.99490.5397.94760.99900.99741.0312.61290.99940.99881.5316.30290.99940.9987

4 结论

利用具有大形变的自然图像、MRI图像、CT图像进行测试，与active demons, diffeomorphic demons算法进行对比分析，利用相关指标来定量评价配准的效果，结果表明，本研究提出的基于局部联合熵梯度的双向多分辨率demons算法的归一化互相关系数、结构相似度最高，均方误差最小，得到的配准效果最佳。该方法能有效的解决大形变场图像配准的问题，具有一定的临床应用价值。