基于盒维数序列变异系数的轴承外圈失效特征

王华中，魏 晖，高志刚

（1.江西科技学院 汽车工程学院，江西 南昌 330098；2.江西科技学院 协同创新中心，江西 南昌 330098）

1 引言

滚动轴承构造由内圈、外圈、滚动体和保持架四种元件组成，是旋转机械的支撑部件，其运行状态会对整机的运行产生重要影响。据统计，旋转机械的故障有30%是由轴承故障引起的[1]，因此对其进行监测与诊断的研究具有重要意义。

轴承失效的基本形式包括磨损失效、疲劳失效、腐蚀失效、断裂失效、压痕失效以及胶合失效等，失效部位主要有内圈、外圈和滚动体等，而诊断方法主要有油液分析技术、噪声监测技术、红外测温技术、振动监测技术、声发射技术以及无损检测技术等。由于滚动轴承运行状态好坏往往直接体现在振动信号中，且振动信号便于在线测定运行工况，工程上一般采用振动监测技术监测和诊断滚动轴承状态。如何从非平稳的状态信号中提取故障信息特征形成待检模式，进而进行模式识别或分类，则成了轴承故障诊断的关键。

可用于轴承状态监测和故障诊断的特征指标有许多，且各个特征指标对轴承健康状态的规律性、敏感性和聚类性不尽相同，包括二十余个时域与频域特征指标[2]。由于外载荷、摩擦力以及随机干扰力的存在，轴承振动呈现出非线性、非平稳的特点，基于时域特征或频域特征的诊断方法存在着原理性的不足。为此国内外学者发展了诸多非线性的方法，如Morlet小波降噪、EEMD、VMD以及分形方法[3-6]。其中，分形特征由于其模式描述和区分能力强、特征参数少而广泛应用于旋转机械的故障诊断[7-9]。

文献[5]采用形态学操作计算分形维数的方法，对实际的滚动轴承正常、滚动体故障、内圈故障和外圈故障信号进行了分析与对比，得出外圈故障的分形维数最低，但未对分形计算后的特征值进行分析；文献[7-9]利用关联维数或广义维数判别滚动轴承故障，但相关分形维数的无标度区间确定及计算开销限制了其应用。此外，目前的研究多采用分形维数作为特征参数静态的刻画轴承失效过程，而轴承振动状态从早期异常到功能失效是一个逐渐劣化的过程，其在轴承全寿命周期内并非平稳的。

2 分形及分数维

2.1 分形的概念

分形定义为“其组成部分和整体以某种方式相似的形”（Benoit Mandelbrot，1986）。1967年 Mandelbrot提出分形的概念，并应用于海岸线的度量，分形理论已广泛应用于计算机图形学、机械工程、物理、化学、生物医学、材料科学、水文地质乃至气象、经济管理等学科领域。分形理论作为一种数学工具，可从时间序列数据中研究复杂系统的分形特征，对于人们理解复杂系统的动力学行为机制提供了分析手段。分形理论的基本内容包括分形集的自相似性与无标度性。这种自相似性表现为在一定标度范围内其形态、功能或信息的自相似；而具有分形特征的物体没有特征尺寸，其形态、内在的复杂程度、不规则性等各种特性在每个层次上均保持一致。这种自相似性可以是严格的，也可以是统计意义上的相似，相应分别称为“有规分形”与“无规分形”。自然界中的大多数分形是无规分形。

2.2 分数维

无规分形广泛存在于各类复杂系统的振动。分数维（分形维数）是分形理论中的主要参数，它定量描述分形集的复杂度与不规则程度。Mandelbort首先提出用分数维来描述分形现象，而非一般拓扑集的整数维。

由于可采用不同的尺度度量分形集，而分数维则表示为度量结果与度量尺度的某种比值，因此分数维有多种定义形式。其中建立在相对比较容易处理的测度概念的基础上的Hausdorff维数（Hausdorff Dimension）是分形理论中一种最基本的分数维，其数学概念清晰，但多数情况下难以计算或估计。工程上多采用盒维数（Box Dimension）、关联维数（Correlation Dimension）以及信息维数（Information Dimension）等，其中盒维数反映了分形集的几何尺度情况，信息维数能够反映出分形集在分布上的信息，而关联维主要描述的是系统在相空间的轨迹的复杂性。由于盒维数计算较为简单，多用于低维时间序列的分析。

3 盒维数的计算及其变异性特征

3.1 盒维数定义及计算

盒维数是根据测度关系求分形集维数的。对于一般点集Ω⊂Rn，如果它可以由Nδ（Ω）个边长为δ的n维超立方体覆盖，定义[10]：

并称其为点集Ω的盒维数。其中，标度δ下的总盒数Nδ（Ω）的计盒方法见式。

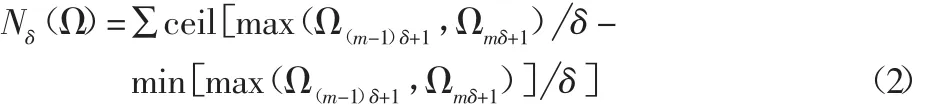
式中：ceil（·）—按+∞方向取整函数，max（·）与min（·）—求序列极大值、极小值函数；cellmax—方格最大边长如图1，δ=10，Nδ=31。

图1 标度δ下的总盒数NδFig.1 Box Number in Scaleδ

因此，盒维数的计算流程，如图2所示。

图 2盒维数计算流程Fig.2 Flow Chart of Box Dimension

3.2 无标度区间的确定

就无规分形而言，自相似性总是存在于一定的尺度范围，即分形无标度区，从lnδ～lnNδ图中确定无标度区是盒维数计算的关键确定无标度区是盒维数计算的关键。目前无标度区的确定方法有相关系数检验法、三折线段拟合法和遗传优化选择算法。相关系数检验法是将数据点进行相关系数检验，若检验能通过，就将该段数据作为无标度区。采用最小二乘拟合+稳健估计选择无标度区间，如图3所示。

图3 无标度区间的确定Fig.3 Identity of Scale-Invariant Region

3.3 平稳性检验与变异性评价

以往的研究多以轴承振动信号的盒维数、信息维、关联维数、广义维数作为故障特征[5-7-10]，静态的分类轴承的故障模式。然而随着故障的发展，其分形维数应为变化的。将分形维数作为一个随机过程，分析序列的平稳性，或能更深刻的描述轴承失效故障的发展。如序列是平稳的，我们可采用一阶矩或二阶矩表征序列的统计特征；如非平稳，则可考虑采用序列的变异性作为失效特征。

平稳性反映了时间序列的内部逻辑性，关于序列平稳性可采用单位根检验判别，如ADF检验（Augmented Dickey-Fuller Test）。ADF是检验序列中是否存在单位根，如不存在则接受序列平稳的假设，如存在则拒绝假设。

当从统计意义上均拒绝了分形维数序列的平稳性假设，那么考察序列的变异性将是合理的。引入变异系数（Coefficientof Variation，C.V），通过二阶矩与一阶矩的关系来刻画这种变异性：

式中：S.D—序列的标准差；

xav—序列的均值。

4 计算结果与比较

为验证分形维数在轴承外圈故障诊断中的有效性，采用美国辛辛那提大学IMS中心的全寿命轴承失效实验[3]的第2组数据作为分析样本，分析盒维数作为特征参数，对Rexnord ZA-2115双列滚子轴承的外圈工作状态进行了仿真。

4.1 分析样本及实验条件

实验时间为2004年2月12日至2004年2月19日，其中，轴承1外圈在2004年2月19日0：02-6：22前后失效[3]。实验条件，如表1所示。实验台及传感器布置，如图4所示。部分数据样本，如图5所示。

表 1实验条件Tab.1 Test Condition

图4 轴承试验台及传感器布置Fig.4 Bearing Test Rig and Sensor Placement

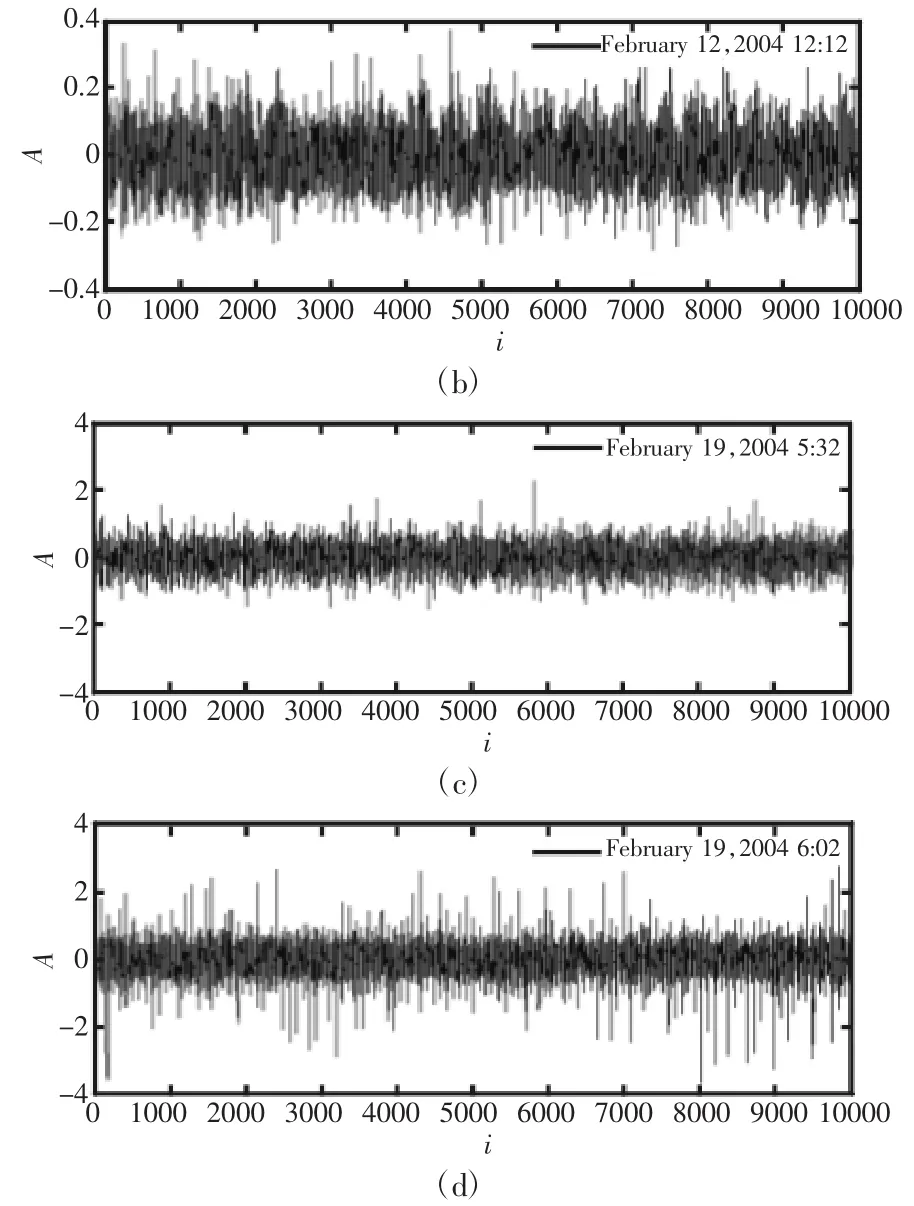
图5 轴承外圈振动样本（局部）Fig.5 Vibration Sample of Outer Race（Partial）

4.2 仿真结果及分析

采用式计算盒维数，主要计算参数选择如下：

式中：cellmax—样本分析的长度。

计算轴承1外圈失效的盒维数，如图6所示。

可得，IMS全寿命轴承失效实验数据的轴承1外圈正常工况与失效工况下振动波形盒维数的均值、标准差、偏度、峰度以及极大值、极小值及变异系数，如表2所示。此外，对图6数据采用ADF进行平稳性的检验，从统计意义上均拒绝了外圈正常状态与失效状态下振动波形盒维数的平稳性假设。但由表2可知，两种状态下的标准差与峰度还是有着较大的差异。如式，引入变异系数来刻画盒维数的特征，可知：外圈正常状态下振动波形盒维数的变异系数约为0.47978%，而失效状态下振动波形盒维数的变异系数为3.18239%，如表2所示。

图6 轴承1的盒维数Fig.6 Box Dimension of Bearing 1

表2 盒维数数据统计Tab.2 Statistical Index of Box Dimensions

5 结论

在轴承失效的判别中引入分形理论，然后选择盒维数作为轴承故障特征，并以IMS的轴承全寿命失效实验数据为样本，对盒维数的轴承外圈失效进行了验证。（1）轴承振动具有分形特征，外圈正常工况与失效工况的盒维数分布在（1.61～1.79）区间，其均值差异不大；（2）外圈正常工况下，盒维数标准差＜0.01；当外圈失效时，盒维数标准差＞0.05；（3）盒维数的时间序列在正常及失效两种状态下均非平稳，但其变异系数差异较大。分析轴承振动盒维数的变异性，或许可以作为轴承外圈失效的判断依据。