系统极化码与非系统极化码的研究现状与发展趋势
王秀敏,吴卓铤,李 君,洪 波,汪晓锋
(中国计量大学 信息工程学院,浙江 杭州 310018)
极化码[1]是由Arikan提出的一种基于信道极化的信道纠错码,其在理论上被证明可达到香浓极限.极化码相比目前被广泛应用的LDPC和Turbo码有着更好的性能以及更低的复杂度,这使得极化码成为当前的一个研究热点.极化码分为非系统极化码与系统极化码.非系统极化码[1]首先被Arikan提出并作为标准的极化码.非系统极化码以一串包含着信息位和冻结位的信息比特作为输入信息输入到编码结构中,编码后的码字不存在原始的信息位.非系统极化码编码之后的码字中,信息位与校验位相互交替,这使得非系统极化码在译码后还需要另外找出相应的信息[2].为了提高极化码的性能,解决非系统极化码的缺陷,Arikan提出了系统极化码[3].系统极化码与非系统极化码主要不同之处在于,系统极化码具备两个输入信号,这两个信号分别从编码结构的两端输入.系统极化码的输出码字中包含了原始的信息位.Arikan在文献[3]中认为系统极化码在SC译码中的误码率比非系统极化码低,且其编码的硬件复杂度理论上与非系统极化码相同.
本文首先介绍了非系统极化码与系统极化码的编码方法.其次介绍现有的基于流水线方法的部分并行非系统极化码编码器的硬件实现方法.接着主要从递归与非递归、并行设计的角度介绍系统极化码的硬件实现方案,并对不同方案进行对比与总结.在介绍完硬件实现方案后,本文通过Matlab仿真验证系统极化码与非系统极化码在SC译码、SCL译码以及BP译码条件下的性能差异.最后,通过总结前面分析的内容,探讨了系统极化码与非系统极化码各自的重要性并提出了一种基于生成矩阵简化的研究方向.
1 极化码编码算法
1.1 非系统极化码
根据文献[1]中对非系统极化码的定义,令极化码码长为N,核矩阵F=[1,0;1,1],极化码的生成矩阵GN可由核矩阵F通过n(n=log2N)阶克罗内克积(Kronecker Product)运算得到,该运算用符号⊗表示,即
GN=F⊗n.
(1)
令U为未编码的信息序列,X为编码后的信息序列.对于非系统极化码,序列U中包含了全部的信息位与冻结位.图1为N=8的非系统极化码编码结构图[1],图中黑色圆点为冻结位.u1~u7作为极化码结构的输入信息,其中u1、u3、u5、u6、u7为信息位,u0、u2、u4为冻结位.经过编码运算得出编码后的序列x0~x7,即有
X=U·G.
(2)
非系统极化码的编码过程与传统的线性分组码类似,编码序列X由未编码序列U与生成矩阵G进行模二累加和获得.所不同的是,非系统极化码编码后的序列不包含原始信息比特.

图1 8位非系统极化码结构图Figure 1 Eight-bit non-system polar encoder structure
1.2 系统极化码
系统极化码与非系统极化码在编码阶段与译码阶段都存在着差异.编码阶段,系统极化码同时由编码结构的两端输入X与U.如图2所示,根据文献[3]中定义,设信息位下标为A={1,3,5,6,7},冻结位下标为B={0,2,4}.则编码结构左边的输入U被分为两部分U={uA,uB},相对应的,X被分为X={xA,xB}.文献[3]中的编码过程可表示为式(3)和式(4):
xA=uA·GAA+uAc·GAcA,
(3)
xB=uA·GAB+uB·GBB.
(4)
其中:GN=[GAA,GAB;GBA,GBB];GAA、GAB、GBA以及GBB分别为GN的一个子矩阵.这些子矩阵分别以A和B作为行列索引从矩阵GN中所得到.例如GAB是由矩阵GN以A作为行索引B作为列索引组成的,即GAB={Gmn:m∈A,n∈B}.式(3)、(4)中,uB存放冻结位信息,xA存放信息位信息,uA与xB为方程中的未知量,系统极化码的编码算法即求出其中的未知量xB.文献[4]中指出,根据矩阵运算法则,只要GAA可逆,xB可表示为式(5).由于GN是一个上三角形矩阵,上述求解xB的过程可通过高斯消去法进行求解.高斯消去法所消耗的计算单元为3log2N,其计算单元消耗远远高于Arikan所提到的理论值Nlog2N[3].

(5)

图2 8位系统极化码结构图Figure 2 Eight-bit system polar encoder structure
在译码阶段,非系统极化码译码时直接输出译码最后的判决结果.而系统极化码在译码得到译码判决结果后,还要将判决结果进行一次非系统极化码的编码运算,其作用可理解为一种极化码编码判决[5].
系统极化码在文献[3]中被证明其误码纠错性能优于非系统极化码,但系统极化码的双向编码结构增加了其硬件实现的复杂度.另一方面,系统极化码译码输出判决阶段还要进行一次非系统极化码编码,这使得系统极化码的输出延迟比非系统极化码高.
2 极化码编码硬件实现方案的研究现状
2.1 非系统极化码硬件实现方案
Arikan在文献[1]中给出了一种完全并行的非系统极化码的编码结构.如图1,当编码信息码长为N时,该编码结构被分为n层(n=log2N).一次编码同时输入N比特信息进行一次性编码并输出N比特编码后码字.其计算复杂度为θ(N·log2N),系统延迟约为n个模二运算的总和.可以看出,随着码长的增加,该编码器的计算复杂度和系统延迟增大趋势明显,这不利于长码长编码.而文献[1]中又指出,极化码码长越长其纠错性能越好.这表明要在实际应用中获得更好的极化码纠错性能,如何从硬件上降低极化码编码器在长码长下的硬件复杂度和系统延迟将是一个关键的问题.
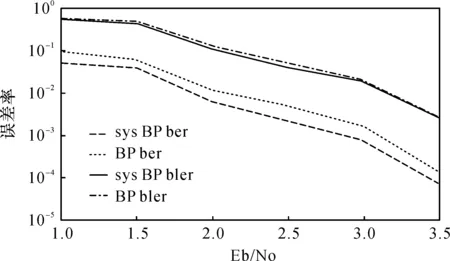
针对长码长非系统极化码编码,文献[6]提出了一种部分并行的极化码编码方案.该方案充分利用了编码结构同一层数据的计算不相互依赖的特性,利用流水线方法将原本的全并行输入结构改为部分并行输入.对于全并行输入,假设输入数据所需的时间为t1,系统编码过程所需时间为t2,则系统的总延迟为(t1+t2).文献[6]中假设每个分段数据输入的时间为t3(t3 目前,非系统极化码已经具备相对成熟的硬件实现基础,由于非系统极化码的编码结构与快速傅里叶变换的结构非常类似,文献[7]借鉴FFT算法设计出了等价于核矩阵F运算结构的PE2,以及并行度为4的PE4.该编码器巧妙地运用先进先出结构(FIFO)来实现极化码结构中不同部分的输入顺序转换.如表1所示为上述方法与文献[1]在码长分别为1 024、4 096以及163 884时的资源消耗情况.图3给出了部分并行编码器[7]在码长为8 192与基于PE2设计的编码器[6]在码长为16 384时的吞吐率以及单位并行度吞吐率(NT)柱形对比图. 表1 计算单元消耗对比图 图3 吞吐率与NT对比图Figure 3 Throughput rate and NT 从表1与图3中可看出,文献[6]与文献[7]中设计的编码器相对于Arikan在文献[1]中设计的编码器在计算单元消耗方面有着显著改进.令文献[7]设计的编码器为Encoder 1,文献[6]中设计的编码器为编码器Encoder 2.则由于Encoder 1中对PE2或PE4有着极高的重复利用率,使得其计算单元消耗小于Encoder 2.另一方面,虽然Encoder 2中的编码整体吞吐率比Encoder 1高,但其单位并行度吞吐率(NT)相对较低.这说明了在相同并行度的条件下Encoder 1的吞吐率性能优于Encoder 2.随后基于PE2的16路并行编码器在文献[8]中被提出,该编码器在码长为8 192时吞吐率可达160 Gb/s.表明了16路并行下的PE2的吞吐率性能远远高于Encoder 2的性能.从以上几种非系统极化码的编码方案中可以看出,非系统极化码的编码技术改进主要是通过分割编码结构,将原本一步完成的工作分成几步完成,虽然这减少编码过程中每一步的运算时间,提高了工作频率的上限,但这将使得编码器在运行初期的数十个周期内输出无意义的信号,以致降低了系统工作的整体稳定性. 系统极化码在编码过程中需要进行双向来回运算,这使得上述非系统极化码编码方案无法直接适用于系统极化码.另外,双向运算大大增加了系统极化码的硬件复杂度.降低系统极化码硬件实现的复杂度,提高系统极化码的编码效率将是系统极化码的主要优化方向.在复杂度方面,目前主要的优化方法有递归编码与非递归编码[4].而在编码效率方面,主要采用部分并行流水线方法. 2.2.1 递归编码与非递归编码 递归编码结构首先由Arikan在文献[3]中提出,文献[4]中提出了递归编码结构的硬件实现方法.系统极化码递归编码将u与x进行L(L=log2N)次的分裂.文献[4]将分裂后的信息表示为式(6)和式(7): (6) (7) rl,2i-1=rl-1,i (8) (9) u′=x′+r. (10) 其中:u′和x′分别为u和x中的一个元素.已知系统极化码中u与x中相同下标的两个元素有且仅有一个已知值,故上述等式只要求得r值,便可根据u′求x′或者根据x′求u′. 该算法中,仅需要计算并存储二叉树图中每一级的rli值便可通过(10)得到编码码字.故该方法仅需2N-1个存储单元分别存储二叉树中的每一个节点.除了顶部节点以外,其他节点均被访问并计算3次, 故其计算单元的消耗为N·(1+log2N).从图4可以看出,该编码的编码结构基于图中单元的运算与分裂.可参考文献[8]中的编码方案,将该单元作为一个基础运算单元,类似于PE2,通过流水线技术进行单步运算,以提高整体的吞吐率. 图4 8位递归结构二叉树图Figure 4 Binary tree diagram of Eight-bit 非递归编码直接通过系统极化码的编码结构进行编码计算.系统极化码编码时行与行之间并不是相互独立的,上面的行在编码的时候依赖于下面行的中间信息.如图2,当编码器计算节点x4时,编码器同时需要节点a和b的信息,其中a由u4与节点b通过模二运算得来,而节点b来源于x6与x7.该过程中,计算x4所需要的信息需要来自下方的x6与x7.文献[4]提出的Encoder A符合了系统极化码的运算特点.其通过由下至上、由已知端到未知端进行横向的逐行编码.每一行除了存储最后的编码结果之外,还需要进行中间结果的储存,如图2中a与b的值,其存储单元消耗为N(1+log2N).相比文献[1]中提出的非系统极化码编码方案,Encoder A消耗了更多的存储单元,但其所需的计算单元与非系统极化码的一致,即Arikan提出的理论值.为了降低存储单元的消耗.文献[9]中在Encoder A的基础上提出了一种减小存储单元消耗的非递归编码器.该编码器采用与Encoder A相同的计算流程,所不同的是,该方法将极化码编码结构分为λ(λ=0,1,2,…,n-1)层,并将每一层的节点按相对独立性划分为2(n-1)-λ块.比如当n=3时,编码结构被划分为3层,第0层的节点分为4块,第1层划分为2块,第2层划分为1块.如图2所示,该算法运行第0层的运行步骤为: 1)将x7传入编码结构右下角的c,d,e中; 2)将x6传入c中并与d进行异或运算,将得到的值赋给b; 3)复用c,将x5的值存入c中并进行后续操作. 该算法采用复用存储单元的方法,每一层的计算仅需要一个块的存储单元.其最终消耗的存储单元为N,相比于Encoder A有了明显的改进. 虽然这些方法有效的降低了式(3)和(4)进行高斯消去法求解的复杂度θ(3log2N).但三种算法的计算单元消耗仍然无法低于θ(N·log2N).这不利于长码长情况下的系统极化码编码器设计.系统极化码的递归与非递归算法中,虽然节省了大量的存储单元,但其设计过程中并未考虑其编码的吞吐率,利用这两种算法与非系统极化码高速编码器的设计思想相结合将是一个重要的研究方向. 2.2.2 系统极化码的部分并行设计 系统极化码的双向运算结构是其进行部分并行设计的难点之一.文献[10]提出了一种基于非系统极化码编码结构的系统极化码单向传播结构.如图5所示,该方法将系统极化码的双向传播改造为与非系统极化码类似的单向传播结构.该编码码步骤如下: 1)将输入u进行一次非系统编码得出码字u′; 2)u′中冻结位所在位置的信息置为0,其他位置的信息保持不变; 3)将u′再次作为输入码字进行非系统极化码编码,最终输出结果即为系统极化码编码码字. 图5 8位单向运算系统极化码编码结构图Figure 5 The polar code structure diagram ofthe 8-bit unidirectional operation system 文献[11]指出,上述单向传播系统极化码编码结构可以看作是两个非系统极化码结构的结合,并以文献[10]作为基础设计出一种单向传播的部分并行系统极化码编码方案.该编码器采用两个非系统极化码编码器串联的方式设计出了多路并行编码器. 表2列出了码长16 384、并行度32的系统与非系统极化码部分并行编码器系统的资源消耗与吞吐率.从表中可以看出,由于文献[11]中的系统极化码编码方案采取了两个非系统极化码编码器,其结构复杂度与运算复杂度都要高于文献[6]中的非极化码编码器.这使得其在各方面的性能都低于文献[6].但相比于文献[3],其资源消耗与吞吐率两方面的性能已经得到了很大的改进. 表2 计算单元消耗对比图 目前,系统极化码的并行设计方案的主要思路是将双向运算转化成单向运算,该方法虽然可行但却大大的增加了系统的复杂度.而系统极化码的递归结构属于单向运算过程,该编码结构将是系统极化码并行设计的基础. 基于以上对系统极化码与非系统极化码硬件实现方案的分析.为了验证两种编码在相同信道条件下的性能差异,本章基于Matlab仿真平台,在其他条件相同的情况下,分别对两种编码在SC译码、SCL译码以及BP译码条件下进行了误码率与误帧率的性能仿真,仿真结果如图6~8,表3给出了具体的仿真方案. 表3 仿真方案详细配置 图6 系统与非系统极化码在BP译码下的性能对比Figure 6 The performance comparison between system and non-system polar code under BP decoding 图7 系统与非系统极化码在SC译码下的性能对比Figure 7 The performance comparison between system and non-system polar code under SC decoding 图8 系统与非系统极化码在SCL译码下的性能比Figure 8 The performance comparison between system and non-system polar code under SCL decoding 从以上的仿真中可以看出,系统极化码性能优于非系统极化码.在未来的极化码应用中,系统极化码终将取代非系统极化码.但由于系统极化码在译码阶段仍然需要进行非系统极化码判决.故对非系统极化码继续研究同样重要.目前,系统极化码的硬件实现方案仍然需要消耗大量硬件资源.系统极化码虽然已经实现了部分并行流水线的结构,但其吞吐率还远比不上非系统极化码.如何提高系统极化码编码吞吐率将是一个研究的热点与难点.极化码属于线性分组码,其编码阶段本质上是生成矩阵G与输入码字的一次模二运算,而极化码的生成矩阵G是由核矩阵F组成,具有一定的规律.如何从矩阵运算的角度找出G矩阵的规律并简化其运算过程将会是接下来研究高速低功耗极化码编码器的另一个突破口. 随着5G时代的到来,当下的通信技术已经越来越无法满足网络流量日益增长的需求.极化码作为5G的控制信道编码方案,其在短码长的性能将更受关注.而极化码的性能与码长成正相关关系,也就是说极化码的码长越短,其性能越差.极化码的级联编码可以有效的提高其短码的性能.文献[12]中,以LDPC短码作为外码,极化码作为内码来提高有限码长的极化码的纠错性能,该级联码在SC译码的条件下相比于传统极化码提高了0.5 dB. 另一方面,深度学习技术已经渗透到了各种传统的工业技术当中,并带来了突破性的成果,极化码的编码结构与深度学习全连接神经网络非常相似,如何建立两者的关系,利用深度学习技术来优化极化码编码技术将是极化码研究的另一个关键问题.

2.2 系统极化码硬件实现方案
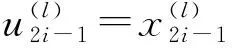
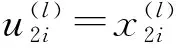
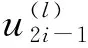





3 系统与非系统极化码性能仿真



4 发展趋势探讨

