圆形煤场煤堆体积快速测量方法
张 森,孔 明,王道档,刘 维,郭天太,赵 军
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
在电厂、粮仓等大型存储基地为了防止煤炭或粮食等受到强光、雨水等的侵蚀而建立圆形的仓库,对其所要的存储的煤炭、粮食等进行保存.其中,圆形煤场因具有储存、缓冲和混煤等多项用途[1],而且相较于其它封闭式仓库,圆形储物仓具有相对用地少,单位面积内存储量大、现代化程度高、对恶劣环境抵抗性强、环境友好等优点,因此圆形储物仓越来越受到燃煤电厂的青睐[2].由于圆形煤场特殊的外形,目前较多圆形煤场储煤量采用估算的方式获取,这与实际情况之间存在较大误差[3].因此,有必要提出一种新的针对圆形煤场煤堆体积计算的测量方案从而快速、准确地获得圆形煤场煤堆的体积和质量,这将有助于国家、企业进行生产计划调整.随着计算机视觉和光学技术的发展,基于机器视觉重建的光学测量系统的研究越来越多——顾超[4]等为了解决传统相位解包时存在的误差传播和测量精度问题,提出一种基于面结构光的双目视觉系统,使用三种频率光栅投射的三频外差相位展开技术,但投射光栅条纹的数目的增多势必会增加测量时间,使系统不能满足实时性的要求.杨德山[5]等提出一种利用手持激光扫描仪来测量堆积物体积的系统,该系统虽然能较快速地计算出堆积物的体积,但由于测量结果很大程度上受外界干扰比较大,因此测量精度较低.熊文涛等[6]通过对误差源的分析,提出一种利用微积分和中心极限定理的方法来实现煤堆体积的自动测量,虽然该方法能在一定程度上实现自动化,但测量过程的耗时较长,且精度较差.陶森柏[7]在三维重构过程中,利用棱锥剖分的方法代替传统的算法,在重构速度上有一定的提升,但过程复杂,实时性较差.
本文提出一种圆形煤场煤堆体积快速测量的方法,即利用多线结构光系统对煤堆进行拍摄采集,利用光条纹中心提取算法,计算出煤堆三维点云数据.而此时的数据不光包括煤堆点云,还有煤场的墙体和屋顶,因此本文提出一种剔除墙体、屋顶点云数据的算法,使得处理后的点云只包括煤堆点.最后又利用Delaunay三角化方法[8-12]对提取出的煤堆点云进行三角可视化操作,并最终计算出煤堆的体积[13-14].
1 测量原理与处理算法
1.1 系统结构
本文提出的圆形煤场煤堆体积快速测量系统如图1,用多线激光器作为系统光源,其发出的25条线激光同时投射在被测物体上,然后通过高精度移动导轨使摄像系统和激光投影系统在同一平面内做无相对运动的移动,在多个位置对被测物进行投射并采集图像,然后将经待测物体调制之后的光条纹的图像进行滤波等预处理,利用条纹中心提取算法和煤堆提取算法即可获取煤堆的三维坐标点云,之后再利用Delaunay三角化方法对提取出的煤堆点云进行三维重构和体积计算.
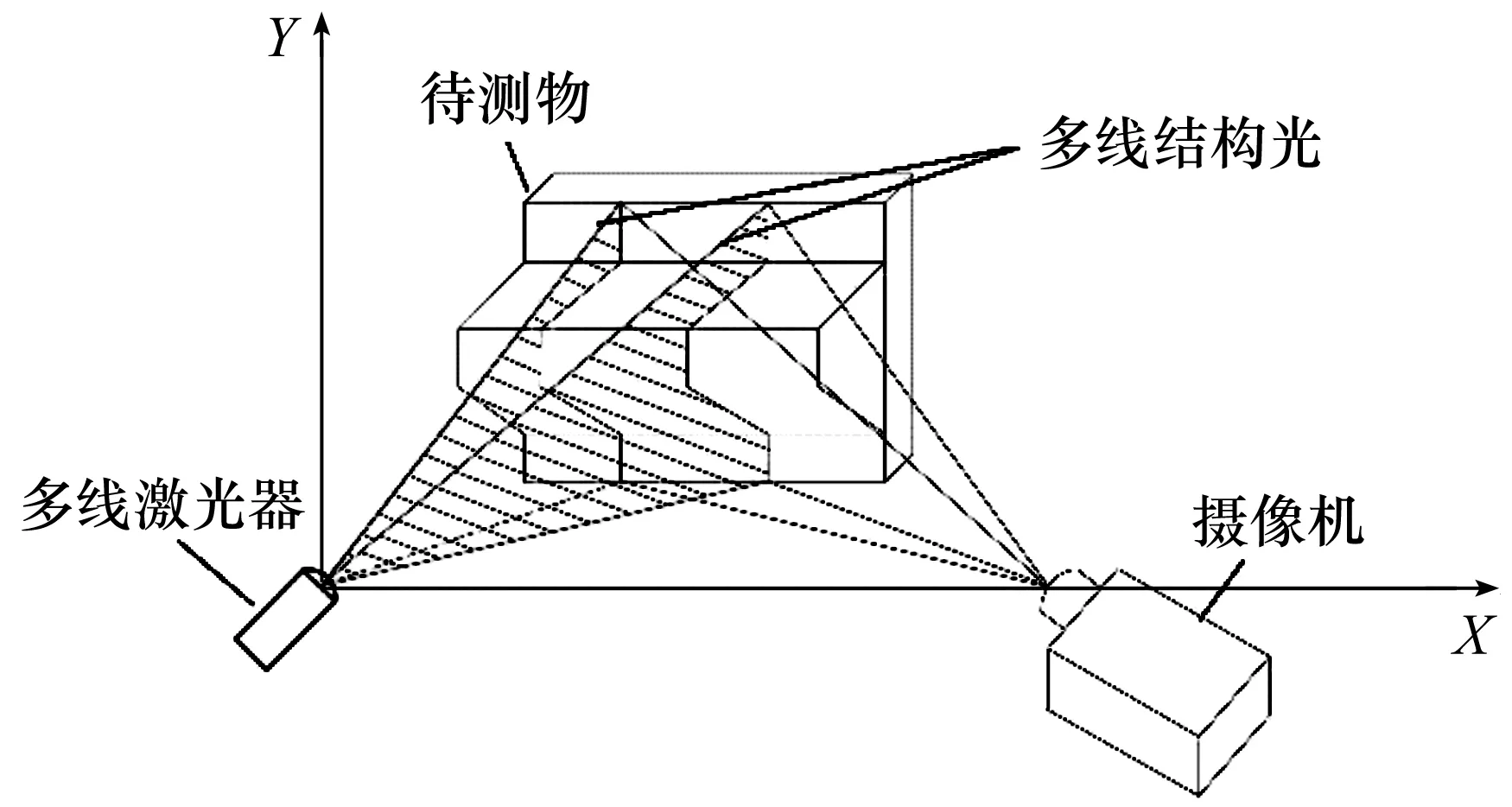
图1 多线激光测量系统Figure 1 Multi-line laser measurement system

图2 系统原理图Figure 2 System schematic diagram
利用激光三角法原理得到待测物体的三维坐标,原理如图2.其中,被测物体位于坐标系XWYWZW内,多线激光器的焦点和相机镜头焦点都位于x轴上,z轴为待测物体高度方向.坐标系xyz是由相机像平面和相机光轴所形成的坐标系,其中相机光轴在z轴上.通过图像像素坐标系→图像物理坐标系→相机坐标系→世界坐标系的转换,可以从采集的图像提取出待测物体的三维坐标值.假设(r,c)和(u,v)分别为图像物理坐标系和像素坐标系中的对应点,根据式(1)建立两者之间的关系为
(1)
式(1)中:(u0,v0)为图像物理坐标系中的原点在像素坐标系中的位置,dx、dy分别为单位像素在图像物理坐标系横、纵轴上的真实大小.
(2)
式(2)中f是相机的焦距,(xc,yc,zc)是相机坐标系中与(r,c)所对应的点.所以图像像素坐标和相机坐标的对应关系为

(3)
式(3)中:s是比例系数,并且有几何关系知像点、物点和原点三点共线,所以可得

(4)
式(4)中:(xc,yc,zc)是处于面阵检测器所形成的坐标系中的任意一点,fx为相机横轴上的焦距,fy为相机纵轴上的焦距.然后通过标定确定线条纹的平面方程如式(5),并与式(4)联立,即可获取待测物体的三维坐标.
axc+byc+czc+d=0.
(5)
1.2 煤堆提取算法
用多线激光测量系统在煤场内部对煤堆进行扫描取点时,不可避免地会采集到煤场的墙体和部分屋顶.在进行煤堆体积计算时,必须把采集到的墙体等多余的点云数据去除,否则将影响点云重构速度,还会对煤堆体积计算带来误差.为了提取煤堆点云,首先需从煤场点云中区分出煤堆和墙体.在本文中将对煤堆的堆积特性分析可知,其在自然堆积状态下总会与地面形成一定的坡度,由此利用墙体和煤堆法向量的差异将其分别提取出来.由于煤场和仓库的形状都是规则的圆形,因此将其投影到X-Y平面上,根据点到圆心的距离来判定某点是否需要保留.算法流程如图3.

图3 体积测量流程图Figure 3 Flow chart of volume measurement
1)根据煤堆、墙体以及地面法向量的差异区分三者——煤堆外表面法向量“倾斜”,墙体法向量是水平方向或者“倾斜”,地面法向量“竖直向上”.若墙体法向量为水平方向,可直接根据法向量来区分煤堆和墙体;若墙体法向量也为“倾斜”,则找到墙体和煤堆所有的法向量,距离煤场中心来说,最外侧的“倾斜”法向量即为墙体.
2)将采集到的煤堆点云(包括墙体)透射到X-Y平面.煤场在X-Y平面上的投影为圆形,可以确定该圆的圆心即煤场的中心.结合前一步骤通过法向量特征提取出的墙体,可得出其到煤场中心的距离R.图中黑色散点区域即为待测煤堆,外侧圆形边框即为待去除墙体.
3)利用平面上点与点之间的距离计算公式来确定该点是否为墙体上一点.

(6)
式(6)中:(x0,y0)为X-Y投影平面的圆心坐标即煤场中心,(x,y)为空间任一点投影到X-Y平面的投影坐标.当且仅当d=R时,该点视为墙体上一点,应该除去;否则,视为煤场内一点,应该保留.
4)对滤除了墙体的煤堆点云数据再进行地面点云去除.之后再进行滤波,该滤波方法结合了直通滤波和统计滤波[11]的优点,能够快速过滤距离目标点较远的离群点,且有效地过滤掉离目标点较近的稀疏点群.
为了验证煤堆提取算法的有效性,利用标准函数生成煤场模拟点云如图4(a)所示,图中柱体模拟煤堆,四周环绕模拟地面和墙体.结合法向量和距离两个条件来进行煤堆提取.对该模拟点云分别进行法向量提取、投影、点云去除等步骤后(图4(b)为中间过程),可提取出模拟煤堆如图4(c).

图4 函数模拟提取过程Figure 4 Function simulation extraction process
1.3 Delaunay三角剖分
在进行煤堆体积计算之前,需要先进行煤堆的三维形貌重构.由于煤堆不存在空间分层遮挡的问题,因此利用投影的方式将点云数据映射到二维平面上.并由区域生长和拓扑关系来得到三角网格,如图5.Delaunay三角剖分[4-8]得到的三角网格具有良好的几何特性——空间中的任意四点不共圆,并且最小角最大,这保证了所得到的三角网格的唯一性和稳定性.并且当某些局部点发生变化时,也只影响其周围所形成的三角形.
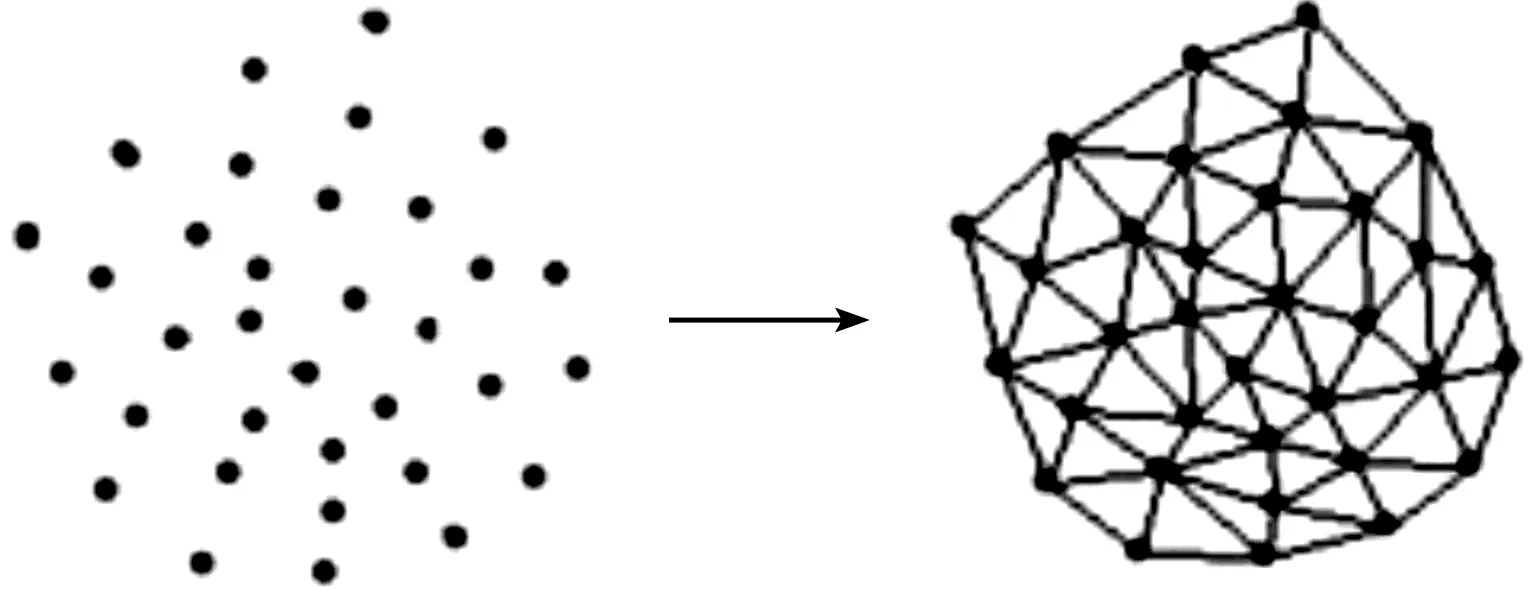
图5 三角剖分原理图Figure 5 Triangulation schematic diagram
在实现煤堆点云数据的三维可视化后,可以利用前述得到的三角化的信息进行煤堆体积计算.将投影在二维平面上的三角形和与之唯一对应的空间三角形对应点相连接,即可得到一个三棱柱,如图6.对所有的三棱柱累加求和,即可得到煤堆的体积.

图6 三棱柱计算模型Figure 6 Three prism calculation model
其中,每一个三棱柱的体积都可被分解为一个正三棱柱和两个四面体体积之和:
(7)
1.4 误差分析
由点云坐标计算公式可知,对点云坐标产生影响的误差主要有:1)测量误差;2)系统安装误差.而作为静态常量的系统安装误差可以通过系统标定来进行消除[15].可利用相对误差E来反映系统测量的准确性.

(8)
式(8)中,xm是测量值,xr是真实值.
为了验证系统的测量可靠性,我们通过多次测量以此得到系统的重复测量误差,并以此来衡量系统的重复性.首先通过贝塞尔公式得到实验的标准差s,然后利用此标准差s除以测量均值,利用此计算结果表征系统的重复性误差er[17-18].

(9)

(10)
2 实验验证
2.1 实验系统介绍
利用上述测量原理设计了基于多线结构光的堆积物体积快速测量系统,系统采用了安福德25条平行线激光器作为激光光源,大恒MER-132-30GC相机,其分辨率1 292(H)×964(V).将激光器和相机安装在同一个移动导轨上,以使相机光心和激光器的透射中心始终在同一平面之上.安装完成之后,对系统进行标定,以确定相机内参并消除安装误差.
2.2 沙堆模拟实验
根据煤堆的自然堆积特性[16],搭建了沙堆模型,如图7,模型上底面直径为31 cm,下底面直径为20 cm,高12 cm.标准沙堆体积为1 000 cm3,堆高5 cm.

图7 沙堆模型实物图Figure 7 Sandpile model physical map

图8 沙堆模型点云Figure 8 Sandpile model point cloud
利用本文搭建的多线结构光测量系统对模型进行扫描测量,生成的沙堆模型点云如图8.先对其进行距离统计滤波[15].之后再对滤波后的沙堆点云进行煤堆提取算法,可得沙堆点云如图9.之后再对提取出来的煤堆点云进行点云三角化处理,并对其体积进行计算.

图9 提取出的沙堆点云Figure 9 A point cloud extracted from a pile of sand
表1为沙堆模型体积计算结果,由式(8)和式(10)可得平均相对误差和重复性误差分别为0.17%与0.17%.结果表明本文提出的基于多线结构光的圆形煤场煤堆体积快速测量系统具有较好的测量精度.并且,该测量系统能够在500 ms内对被测对象进行三维重构和体积计算,在保证精度的同时,大大地缩短了测量时间,提高了测量的效率.

表1 沙堆体积测量结果

图10 沙堆模型体积测量相对误差Figure 10 Relative error of volume measurement of sand pile model
3 结语
本文提出了一种圆形煤场煤堆体积快速测量方法,解决了圆形煤场煤堆体积的准确实时测量问题.即:利用光条中心提取算法将多线结构光测量系统拍摄的煤场图片转换为煤场点云数据;利用煤堆提取算法,能够准确地去除墙体等环境点云的影响,从而提取出煤堆点云,并通过Delaunay三角剖分实现煤堆点云的三维重构可视化及煤堆体积计算.圆形容器沙堆实验结果表明该测量系统的平均相对误差和重复测量误差仅为0.17%和0.17%,测量时间为500 ms,能够实现快速、准确地测量.结果表明,利用本文提出的多线结构光测量系统能够完成圆形煤场煤堆体积准确、快速测量.

