基于CATIA的车辆相对于路边石通过性的参数化分析

王志平，孙喜冬

（长城汽车股份有限公司技术中心，河北 保定 071000）

前言

随着制造业的快速发展，车辆保有量逐年增加，社区及停车场的停车位也逐渐紧张，非机动车道停车位及人行道临时停车位便应运而生，以减少拥堵，缓解停车压力。

其中，非机动车道车位因无台阶且停放、取用方便而供不应求，其他车辆只能停靠人行道临时车位，但此种车位通常位于落差较高的路边石之上，如图1所示，故车辆需具有较好的通过性参数才能方便的进入此类车位，本文提到的参数化模型就可以帮助驾车司机快速判断所驾车辆能否无损的进入临时车位。

图1 位于路边石上方的停车位

1 路边石高度测量及统计

通过对哈弗技术中心周边 4个路段路边石进行抽样测量，其中每个路段各随机测量18处，统计可知：厂区内平均高度为161.1mm；厂区外平均高度分别为农研所路203.1mm，朝阳南大街186.4mm和南二环149.1mm，其中，农研所路路段最高，而南二环（保沧线）路段最低。

并且，下水口附近路边石高度较高，而路口附近相对较低，若要车辆无损的驶上各路段人行道进入临时停车位，则其前后悬高度、纵向通过角、最小离地间隙、轴下离地间隙等均需满足特定要求。

2 路边石通过性初步分析

由于路边石呈阶梯状，故接近角、离去角不会对车辆的通过性产生影响。

影响较大的因素主要有前后悬高度、纵向通过角、最小离地间隙、轴下离地间隙等，故以下分别对车辆的这几项参数进行初步判断分析。

2.1 前、后悬高度

车辆若想无损的进入临时车位，前、后悬高度为其重要影响因素，需要两者中至少一项高度不低于各个路段的最高平均高度，根据前文统计结果（平均最高高度 203.1mm），其前悬或后悬的高度至少有一项不低于203.1mm。

2.2 纵向通过角

在车辆驶上或驶离路边石的过程中，其与车辆底盘的间隙为线性减小或增加的状态，且其边缘多为直角（90°），远大于普通车辆的纵向通过角（通常为25°左右），如图2所示，故在车辆轴间离地间隙满足要求的前提下，纵向通过角对车辆的通过性将不会有影响。

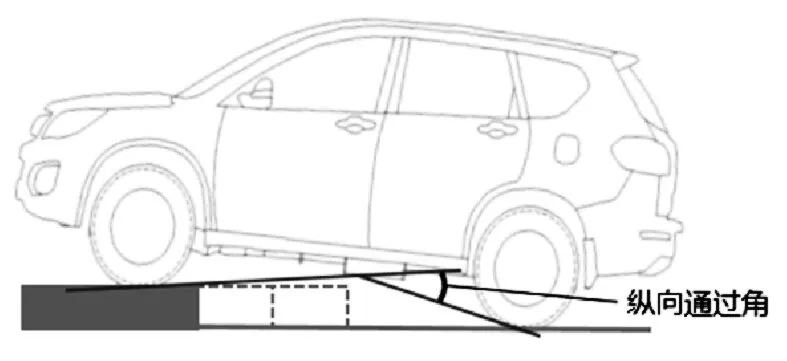
图2 车辆纵向通过角示意图

2.3 最小离地间隙

因路边石的阶梯状结构，在正向（或倒车）驶上路边石的过程中，由于其与车辆底盘的间隙为线性减小，当后轮（或前轮）刚接触其直角边沿时，路边石与底盘距离最近，如图3所示，故可通过校核此状态下的最小离地间隙大小，以判断车辆是否满足间隙要求。

图3 车辆正向驶上路边石状态示意图

2.4 轴下离地间隙

另外，车辆单侧车轮位于路边石上时与正向（或倒车）驶上路边石类似，当路边石接近另一侧车轮内侧时与底盘距离最近，而通常轴下离地间隙不低于最小离地间隙，故仅校核车辆最小离地间隙即可。

2.5 初步分析总结

通过分析可知，接近角、离去角、纵向通过角、轴下离地间隙等不会对车辆的通过性产生直接影响，判断某辆车是否可以无损驶上路边石进入临时车位，只需要校核其前悬高度、后悬高度、最小离地间隙即可。

车辆的前、后悬高度及最小离地间隙等可通过官方宣传资料获得，但由于每辆车的轴距和轮胎型号各不相同，其通过路边石所需的离地间隙也将有较大差异，故其最小离地间隙不一定能满足驶上路边石的要求。

若要判断其最小离地间隙能否满足通过要求，车辆正向（或倒车）驶上路边石时，测量后轮（或前轮）内侧刚与路边石接触时的路边石外沿与虚拟地面（左右两侧前、后轮静负荷半径公切线所确定的平面）之间的距离即可，现利用CATIA软件制作此状态下的简易参数化模型，仅需简便的操作即可快速得知某辆车能够无损通过路边石所需的最小离地间隙数值。

3 CATIA中相关参数化测量模型绘制

首先，打开 CATIA软件，进入“创成式外形设计”（Generative Shape Design）模块，点击“公式”按钮，弹出“公式”对话框，新建4个长度类型参数，分别命名为“石上车轮静负荷半径”“轴距”“石下车轮静负荷半径”“最小离地间隙”，并分别赋值 300mm、2700mm、300mm以及0mm，点击“确定”后可看到左侧产品树中出现刚创建的参数，如图4所示。

图4 产品树中新建参数

其次，以yz平面为基准面，进入“草图”，绘制如图5所示图形，然后对图形进行尺寸及几何约束，石上车轮静负荷半径圆F与石下车轮静负荷半径圆G均为300mm，轴距FG长度为 2700mm，路边石台阶 AB与 CD长度均为3000mm，台阶高为203.1mm，地面DE长度为1000mm，其中圆F与AB相切，圆G与DE相切，圆G与B点相合，且虚拟地面线PQ分别与圆F以及圆G相切于P、Q点。

图5 添加约束后图形

再次，将创建的参数与草图进行参数化结合，双击圆 F的尺寸标注“半径300”，弹出“约束定义”对话框，在半径输入框中右击鼠标，选择“编辑公式”选项，弹出“公式编辑器”对话框，找到“长度”项目下的“石上车轮静负荷半径”并双击，输入框中将出现“`石上车轮静负荷半径`”字样，如图6所示，点击“确定”关闭“公式编辑器”对话框，再点击“确定”关闭“约束定义”对话框，“半径300”尺寸约束末尾出现f（x）标识表示参数化公式编辑成功，同理对圆G以及轴距FG进行参数化公式编辑，令其分别与‘石下车轮静负荷半径’‘轴距’进行参数化关联，尺寸全部参数化编辑后，最终草图如图7所示。

图6 公式编辑器对话框

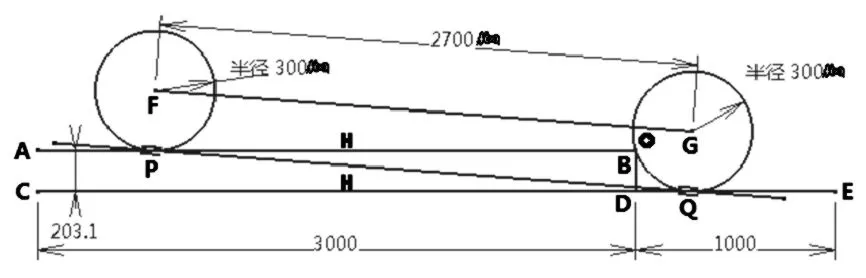
图7 参数化公式编辑后的草图

图8 为最小离地间隙添加公式

最后，完成各项参数化编辑之后的软件界面如图9所示，将参数化编辑完成后的CATIA文件进行重命名后保存备用。

4 标杆车通过性校核及模型验证

为验证此参数模型的可行性，现对某品牌车型进行校核分析，此车为中大型 SUV，其轴距为 2790mm，轮距为1585mm，前后轮胎型号均为 265/65 R17，最小离地间隙为215mm(满载)，根据国标《GB/T 2978-2014轿车轮胎规格、尺寸、气压与负荷》，可知其轮胎静负荷半径为350mm。

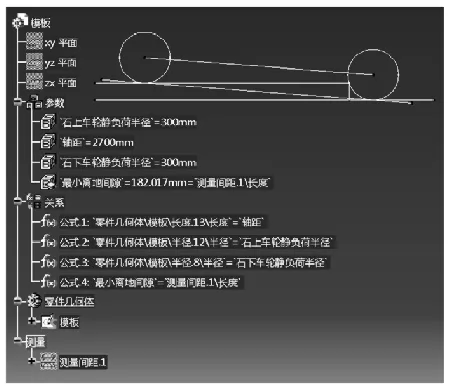
图9 完成参数化编辑后的模型界面

根据之前的分析结论，仅需分析前悬高度、后悬高度以及最小离地间隙等是否满足此种轴距和轮胎型号下的通过性即可。

4.1 前、后悬高度校核

经测量，此标杆车前悬高度约为266mm，后悬高度约为221mm，均高于之前统计的路边石最高平均高度203.1mm，故前、后悬高度均满足要求，即正向或倒车驶向路边石均可满足不碰撞前悬和后悬的要求。

4.2 最小离地间隙校核

打开之前完成的参数化模型，双击“参数”中的“石上车轮静负荷半径”“轴距”和“石下车轮静负荷半径”，将其分别改为“350mm”“2790mm”“350mm”，然后在“测量”中的“测量间距.1”上右击鼠标，单击弹出菜单中的“本地更新”，最后，参数中的“最小离地间隙”值即为此标杆车通过路边石所需的最小离地间隙值180.364mm，如图10所示，小于车辆的实际最小离地间隙215mm，故满足通过性要求。

图10 参数修改及最终测量结果

4.3 标杆车通过性分析总结

通过计算分析，可知此款车型前、后悬高度均高于路边石高度，且实车最小离地间隙大于通过路边石所需的最小离地间隙，故其能够满足各类路边石的通过性要求。

5 结论

本文中介绍的基于 CATIA的简易模型仅利用简单的车型参数（轴距和车轮型号）就能够快速判断车辆是否可以顺利并且无损的通过各类路边石，为驾车司机寻找临时停车位提供便利。

并且，此简易CATIA模型可为底盘开发人员规划新品车型的通过性几何参数时提供参考，以增强车辆的复杂路况通过性，也可一定程度上提高车型的竞争力。