滑动摩擦力疑难问题解析

牛成新

摘要：滑动摩擦力是高中力学的重要组成，是解决动力学问题的重要一环，同时也是学生学习的难点，尤其是方向的判断。本文通过三个疑难问题，剖析了滑动摩擦力大小与方向的分析方法。

关键词：滑动摩擦力；产生条件；相对速度；正压力

中图分类号：P315.2

文献标识码：A

文章编号：1672 -1578（ 2018） 02 - 0217 - 01

摩擦力是高中力学的重点和难点内容之一，也是解决牛顿运动定律、动量、能量等知识的基础，在教学中，许多老师对摩擦力的讲解非常重视，即利用实验进行演示，还借助生活中的现象进行说明，希望学生能够深入理解，但是学生在处理与摩擦力相关的问题时，仍然会出现很多错误，特别对一些疑难问题更是错漏百出，笔者将通过实际教学中遇到的问题，就滑动摩擦力的方向和大小进行探讨。

1.滑动摩擦力有关的基本概念

（1）定义：两个直接接触的物体，当它们之间发生相对运动时，在接触面上就会产生一种阻碍相对运动的力，该力叫滑动摩擦力。

（2）产生条件：①直接接触的物体，接触面粗糙，即有摩擦因数μ，光滑时没有摩擦力；②有正压力F_N；③有相对运动。以上三个条件中，缺少任何一个就不能产生摩擦力，这也是判断摩擦力是否产生的依据。

（3）大小和方向：滑动摩擦力的大小f=μF_N，一定不能理解为f=μmg，因为在很多问题中F_N不等于mg；滑动摩擦力的方向与物体相对运动的方向相反。

2.物体多个面上受滑动摩擦力问题

滑动摩擦力大小由f=μF_N计算，看似简单，但在有些问题中，物体空间受力，使物体不同的接触面有挤压，产生两个以上的摩擦力，学生在处理这种问题时，受力分析不清楚，容易导致错误。突破这一难点的关键是进行图形转换，将立体图转化成一副或多副平面图，在平面图上，把外力沿垂直于接触面和平行于接触面方向分解，利用平衡条件或牛顿第二定律可求得F_N，进而求f。

例1建筑工人为了方便将陶瓷水管由高处送到低处，设计了如图1所示的简易滑轨，两根钢管互相平行斜靠在墙壁上，把陶瓷水管放在上面滑下，实际操作时发现陶瓷水管滑到底端时速度过大，有可能摔坏，为了防止陶瓷水管摔坏，下列措施可行的是

（ ）

A.在陶瓷水管内放一块砖。

B.减少两钢管间的距离。

C.增加两钢管间的距离。

D.用更长的钢管，减小钢管与地面的倾角。

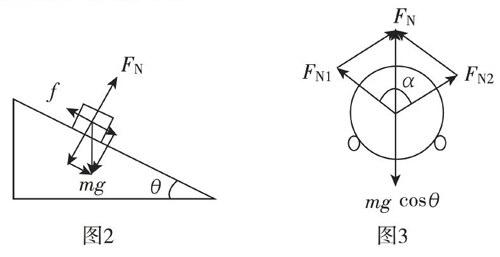
分析：本题的难点在于陶瓷管空间受力，沿斜面方向受两个摩擦力，所以，理清受力是解决此问题的关键，将陶瓷管等效成斜面上的物体，受力如图2，再画出垂直斜面的截面图如图3。

解答：答案C、D。A、在陶瓷水管内放置砖块，增大了整体的质量，重力沿钢管的分力与摩擦力同比增大，加速度不变，陶瓷水管滑到低端时速度不变，故A项措施不可行。BC、适当增加两钢管间的距离，陶瓷水管受到两根钢管支持力的夹角α增大，F_N不变，F_N1、F_N2都增大，而摩擦力f=μF_N1+μF_N2增大，即适当增加两钢管间的距离可以在不改变重力分量的情况下增加摩擦力，陶瓷水管滑到底端的的速度减小。反之，适当减小两钢管间的距离，钢管滑到底端的速度就会增加，故B项措施不可行，C项措施可行。D、用两根更长的钢管，以减少钢管与水平面的夹角θ，陶瓷水管受到的钢管的支持力F_N增大，即F_N1，、F_N2都增大，而摩擦力f=μF_N1+μF_N2增大，与mgsinθ更接近，加速度更小，由运动学知识可得水管滑到底端时速度减小，故D项措施可行。

3.滑动摩擦力方向问题

判断滑动摩擦力方向的方法①选研究对象（受摩擦力作用的物体）；②选与研究对象接触的物体为参考系；③找出研究对象相对参考系的速度方向；④滑动摩擦力与速度的方向相反。在教学中，我们做了这样细致的分解，但学生还是容易出错，究其原因，在于不能准确找出“研究对象相对参考系的速度方向”。

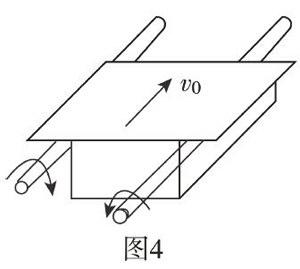
例2一个质量的钢件，架在两根完全相同的、平行的长直圆柱上，如图4所示，钢件的中心与两柱等距，两柱的轴线在同一水平面内，圆柱的半径r=0.025m，钢件与圆柱间的滑动摩擦系数μ=0.20，两圆柱各绕自己的轴线做转向相反的转动，角速度ω=40rad/s，若沿平行于柱轴方向施加力推着钢件做速度为vo=0.05m/s的匀速运动，设钢件左右受光滑槽限制（图中未画出），不发生横向运动g取lO m/s2.求推力是多大？

分析：圆柱对钢件的摩擦力方向不沿轴线方向，因为以圆柱接触点为参考系，钢件与圆柱接触的部分，一方面有沿圆柱轴线的速度，另一方面有垂直于圆柱轴线方向的速度，求出合速度的方向，即可以知道摩擦力的方向，两个摩擦力大小和方向关于轴线对称，所以F=2fcosa（α为圆柱与钢件接触部分的相对速度与轴线方向的夹角）。

解答：每根圆柱所受的压力均等于mg，所以每根圆柱对钢件的滑动摩擦力f=μ·（

）= 20N。对刚件左侧与圆柱的接触点，相对左圆柱运动情况如图5，f的方向与相对于圆柱的速度v方向相反，所以圆柱与钢件接触部分的速度与轴线方向的夹角α满足cotα=（

）=0.05，因为v₀≤ω·r，所以cosα≈cotα=0.05而f与轴线之v₀。间的夹角也为α，在水平面内，根据力的平衡条件可得F=2flcosα=2 x20 x0.05 =2.ON。

例3如图6所示，生产车间有两个相互垂直且等高的水平传送带甲和乙，甲传送带的速度为vo，乙传送带的速度为√3v₀，小工件离开甲前与甲的速度相同，并平稳地传到乙上，工件与乙之间的动摩擦因数为μ，乙的宽度足够大，重力加速度为g。下列关于工件在乙上运动的说法正确的是

（

）

A.在地面上看，工件的运动轨迹是曲线

B.工件在乙上滑过的时间为（ ）

C.工件在乙上侧向滑过的距离（ ）

D.工件在乙上相对运动过程中，摩擦力对工件做功为0

分析：本题的难点在于深刻理解摩擦力的方向一定是与摩擦力的施力物体相对运动的方向相反。

解答：答案A、C。A、如图7所示，滑块相对传送带乙的速度是v₀与

的合速度v，摩擦力的方向与v反向，在地面参考系中，物體的速度为vo，则摩擦力和工件初速度不共线，

综上所述，只有把握滑动摩擦力产生的条件，并能准确进行受力分析和相对速度的判断，滑动摩擦力大小和方向问题必然迎刃而解。

参考文献：

[1] 贺德宏，摩擦力求解中的两个问题[J].新乡教育学院学报.2007，20（4）152 -153.