分离流动诱发的失速颤振和锁频现象研究
李国俊,白俊强,唐长红,李宇飞,刘 南
(1.西北工业大学 航空学院,西安 710072;2.中航工业空气动力研究院,沈阳 110034)
失速颤振及其伴随的分离流动等复杂流动现象对飞行器的飞行性能和飞行安全有一定程度的影响,但是研究人员对失速颤振的发生机理仍然缺乏系统的认识和深入的研究。通常在失速颤振问题研究中,与失速颤振相关的动态失速气动力现象是风洞实验和数值模拟的关注重点。虽然近些年来针对失速颤振本身的研究逐渐增多,但是相比于广泛存在的各种各样的失速颤振现象,这些研究还是远远不够的[1]。
早在第一次世界大战之前,飞机机翼和尾翼的失速颤振现象就已经引起研究人员的注意[2]。从20世纪40年代开始,国内外研究工作者开展了一系列关于失速颤振以及与之密切相关的动态失速现象的研究[3-7],获得了许多有价值的结论。通过研究发现,失速颤振是一种由动态失速和机翼自身的弹性力、惯性力耦合产生的有限振幅的自激振荡现象。在机翼振动过程中,伴随着升力面上的大面积动态流动分离以及再附现象,此时升力面处于失速攻角附近,气动力的非线性很强,是一种严重的气动弹性不稳定现象。与经典颤振相比,能量从气流中传输到振动机翼上的机理,既不依赖于两阶模态的弹性耦合或空气动力学耦合,也不依赖于位移与其气动力响应之间的相位滞后,而是与动态失速和分离流动密切相关。
早期针对失速颤振进行数值模拟大多偏向于计算精度验证,随着研究的深入,研究工作者的研究重点逐渐偏向于失速颤振现象及其诱发机理的研究。近些年来,Dimitriadis等[8-11]开展了一系列关于失速颤振的风洞实验,并采用fsiFoam进行了数值模拟,深入分析了NACA0012翼型的失速颤振现象以及分岔特性。而国内早在2002年,金琰等采用非定常RANS方程结合低雷诺数两方程q-ω湍流模型对NACA0015翼型的失速颤振现象进行了研究。目前在失速颤振现象研究方面,大量的研究结果表明基于非定常RANS方程的气弹求解器足以捕捉与失速颤振相关的关键流动特性和物理现象。
在特定的流动情况下,当分离漩涡的脱落频率接近结构自然频率时,会发生频率锁定(frequency lock-in)现象[12]。在频率锁定范围内,结构响应的幅值会显著增加从而引起结构疲劳甚至失效。目前大多数针对锁频现象的研究主要集中在圆柱绕流中,只有少数研究涉及机翼在涡致振动时出现的锁频现象。Tang等[13]开展了一系列NACA0012翼型在大攻角和高雷诺数下有关锁频现象的风洞实验,研究结果表明NACA0012翼型在给定的强迫运动幅值和频率下呈现出“V”形锁频区。Zhu等[14]采用数值模拟方法研究了一个薄翼型的锁频现象。Young等[15-17]针对NACA0012翼型在浮沉运动中发生的锁频现象进行了研究,目的在于实现翼型推进效率的最大化。上述工作大多是针对强迫运动中的锁频现象进行研究,鲜有涉及自由振动中的锁频现象。
本文基于非定常RANS方程和结构运动方程,建立时域气动弹性分析方法。首先验证了本文采用的非定常气动力求解器模拟动态失速和预测锁频区域的可靠性。其次,使用该方法对翼型剖面为NACA23012翼型的刚性矩形机翼的颤振边界进行验证。在此基础上,改变初始攻角和自由来流速度,对该矩形机翼的失速颤振问题进行数值模拟,分析失速颤振的流动特性和诱发机制,并对失速颤振中出现的分岔和锁频现象进行了研究。
1 流场求解
1.1 非定常气动力求解
本文采用课题组自研的CFD代码-TeAM求解非定常气动力,其控制方程是三维可压缩非定常积分形式的N-S方程,其直角坐标系的守恒形式积分方程为
(1)
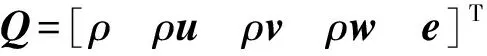
1.2 动态失速气动力响应预测
准确预测动态失速的气动力响应是研究失速颤振现象的前提。本文拟采用非定常RANS方程对NACA0012翼型的动态失速气动力响应进行数值模拟,并与实验结果[18]进行对比,以验证其预测动态失速现象的精度。
实验给定翼型弦长为61 cm,马赫数Ma=0.293,雷诺数Re=3 758 528。翼型强迫振动的攻角随时间的变化方程为α(t)=α0+αmsin(ωt),k=ωb/V∞,其中α0为翼型初始攻角,αm为翼型强迫振动振幅,ω为翼型强迫振动角频率,参考长度b为翼型的半弦长,k为减缩频率。翼型绕自身的1/4弦线做正弦运动,选定翼型的运动规律为:α0=15°,αm=5°,k=0.202 4。计算所用网格如图1所示。

图1 NACA0012翼型网格示意图Fig.1 Mesh for NACA0012 airfoil
图2、图3分别为NACA0012翼型的非定常升力系数和力矩系数随攻角变化曲线,图中实线是本文结果,三角形为风洞实验结果。从图中结果可知,本文求解得到的结果和风洞实验结果基本吻合,表明本文采用的非定常气动力求解器可以捕捉动态失速的主要物理特征,适用于模拟失速颤振中的非定常气动力。

图2 NACA0012翼型升力系数随攻角变化曲线Fig.2 Lift Coefficient versus AOA of NACA0012 airfoil

图3 NACA0012翼型力矩系数随攻角变化曲线Fig.3 Moment Coefficient versus AOA of NACA0012 airfoil
1.3 锁频区域预测
为了确保本文采用的求解器可以应用于失速颤振中的锁频现象研究,对在不同强迫运动规律下NACA0012翼型的锁频区域进行预测,并与文献结果进行对比。NACA0012翼型的弦长为0.255 3 m,展长为0.52 m,翼型绕自身的1/4弦线做正弦运动。测定锁频区域的计算状态为:雷诺数Re=200 000,初始攻角α=40°。计算所用网格采用和1.2节中相同的网格分布,锁频区域对比结果如图4所示。

图4 NACA0012翼型锁频区域Fig.4 The lock-in region of NACA0012 airfoil
图4中的虚线代表Besem等采用谐波平衡求解器得到的锁频区域,圆点表示本文在给定强迫运动规律下发生锁频的结果,三角形点表示不发生锁频的结果。图中的横轴表示无量纲频率fenforce/fshed,即强迫运动频率与固定状态下NACA0012翼型的漩涡脱落频率之比,其中fshed=11.617 1 Hz;纵轴表示强迫运动的幅值。从图中可以看出,本文预测得到的锁频区域与文献结果一致,可以应用于失速颤振中的锁频现象研究。
2 结构运动方程
本文以具有浮沉h和俯仰α两个自由度的典型的二元翼段作为颤振的研究对象,其无量纲形式的结构运动方程为
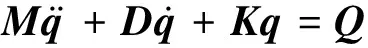
(2)
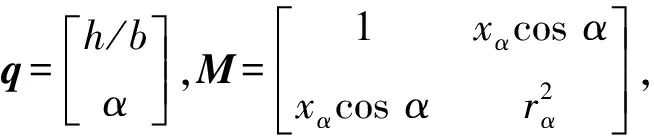

(3)
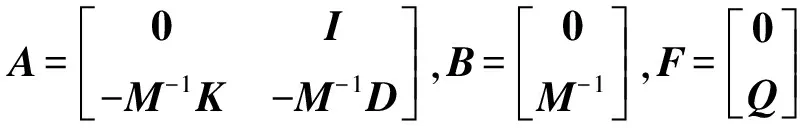
本文采用基于预估-校正技术的四阶隐式Adams线性多步法[19]对式(3)进行时域推进求解
(4)
该方法既保证了方程的求解效率,又具有较好的鲁棒性。
3 算例与分析
3.1 颤振边界预测
Bollay等[21]在哈佛大学的低速风洞中对剖面翼型为NACA23012的矩形机翼的失速颤振特性进行了研究。该机翼模型材料为红木,机翼展长为1 m,弦长为0.171 45 m,实验所用结构参数为:xα=0.228,ωh=80.3 rad/s,ωα=87.2 rad/s,μ=161.2,其中rα按照文献给定为0.5[22],弹性轴即旋转中心位于弦长的35.5%处。
采用本文建立的时域气动弹性分析方法对具有浮沉和俯仰两自由度的NACA23012翼型的颤振边界进行预测,以验证本文建立的颤振数值模拟方法的可靠性。计算所用网格如图5所示。
图6和图7分别展示了NACA23012翼型在给定计算状态下的颤振速度边界和频率边界。其中实线为本文预测得到的颤振边界,虚线为实验结果。数值模拟结果表明,本文预测得到的颤振速度边界和实验结果吻合较好。从图7可知,当α<15°时,颤振频率随着初始攻角的增大而增大;当15°<α<17°时,颤振频率突然下降,其结果接近翼型的结构固有频率;当α>17°时,颤振频率又突然增大。
3.2 失速颤振的流动特性和诱发机制研究
为了探究失速颤振的触发机制,选取初始攻角α=15°、自由来流速度v=17 m/s时的响应作为分析对象。首先对该状态下的结构运动响应和流动特性进行分析,确认机翼此时发生失速颤振,翼型的浮沉运动响应和俯仰运动响应分别如图8和图9所示。从图中可以看出,浮沉位移很小,振幅不超过10 mm,而俯仰位移较大,振幅在10°左右。结合图10中翼型的静态升力曲线可以得知,此时翼型的有效攻角在其静态失速攻角附近上下变化。

图5 NACA23012翼型网格示意图Fig.5 Mesh for NACA23012 airfoil

图6 NACA23012翼型颤振速度边界Fig.6 Flutter speed boundary of NACA23012 airfoil

图7 NACA23012翼型颤振频率边界Fig.7 Flutter frequency boundary of NACA23012 airfoil
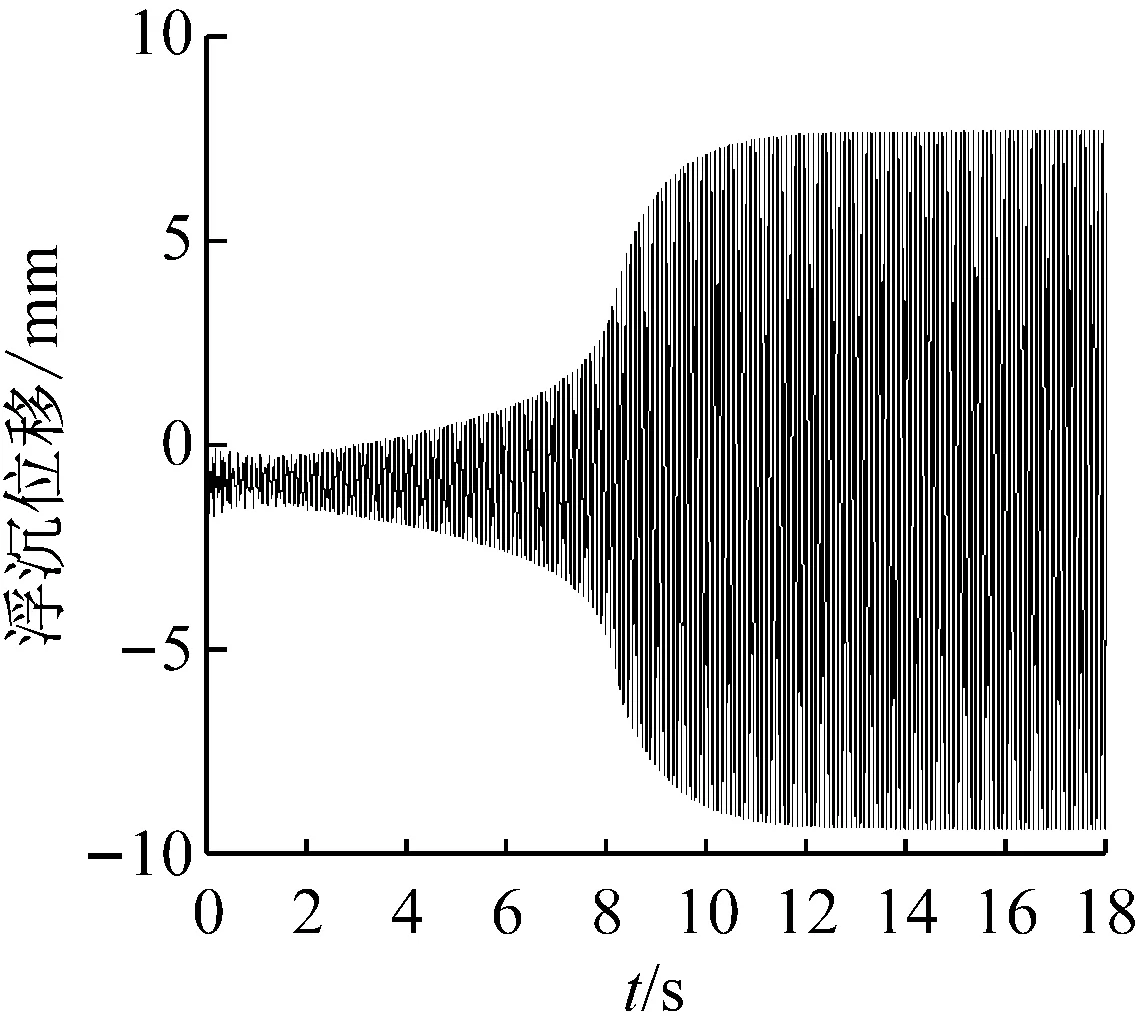
图8 初始攻角α=15°、自由来流速度v=17 m/s时浮沉运动响应
Fig.8 Plunging response atα=15° andv=17 m/s
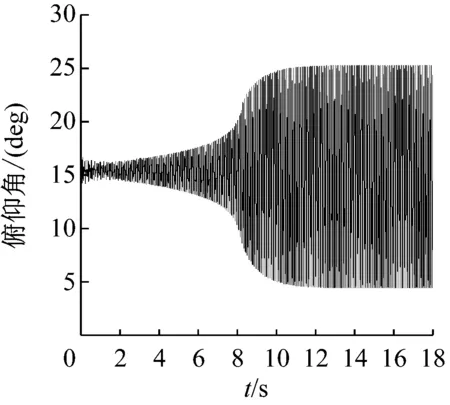
图9 初始攻角α=15°、自由来流速度v=17 m/s时俯仰运动响应
Fig.9 Pitching response atα=15° andv=17 m/s
图10 NACA23012翼型静态升力系数随攻角变化曲线
Fig.10 Static lift coefficient versus AOA of NACA23012 airfoil
图11和图12展示了气动力系数随瞬时攻角变化曲线,结果表明,升力系数并未在静态失速攻角处出现陡降,而是随着俯仰位移的增大而增大,直至在正向最大攻角处(26°)出现跳跃,力矩系数则表现出类似的变化。因为翼型在浮沉自由度上的位移很小,对翼型整体做功贡献很小,因此忽略浮沉自由度的做功,仅对一个周期内的俯仰运动和力矩进行积分得到力矩做功为0.010 58 N·m,此时机翼的非线性气动力和自身的弹性力、惯性力耦合,从气流中吸收能量从而产生有限振幅的自激振荡现象,即失速颤振。

图11 升力系数随瞬时攻角变化曲线Fig.11 Lift coefficient versus instantaneous AOA

图12 升力系数随瞬时攻角变化曲线Fig.12 Moment coefficient versus instantaneous AOA
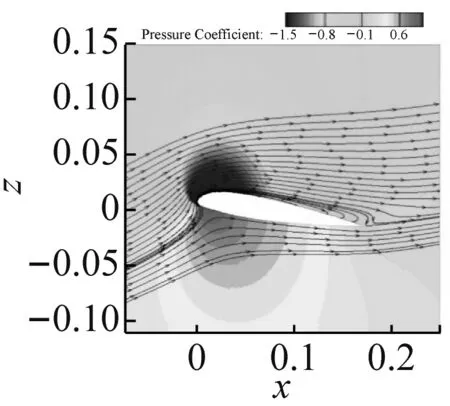
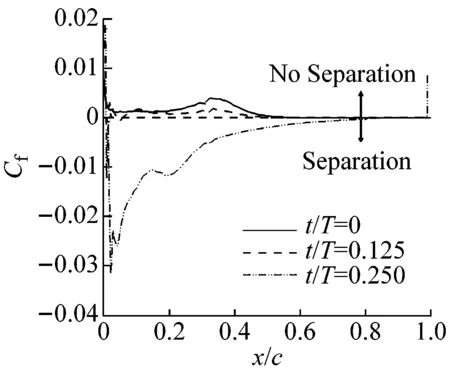
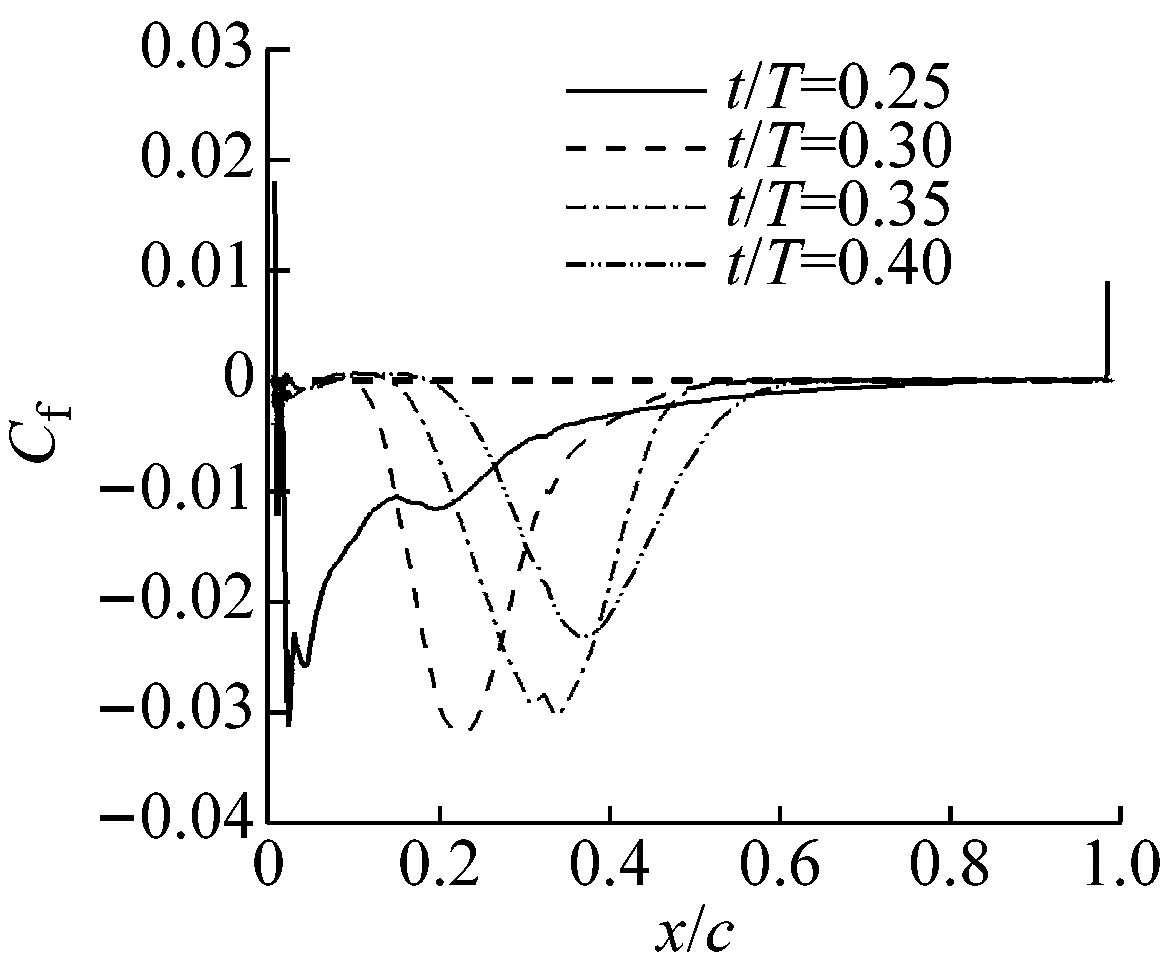
图13为一个周期内不同时刻的瞬态流场,其中背景云图为压力系数云图,t/T代表一个周期内的无量纲时刻。图14为不同时刻的上表面摩阻系数分布。结合图13和图14对不同时刻的流场和气动力变化进行分析,可以将一个周期内的流场现象分为三个大的阶段:
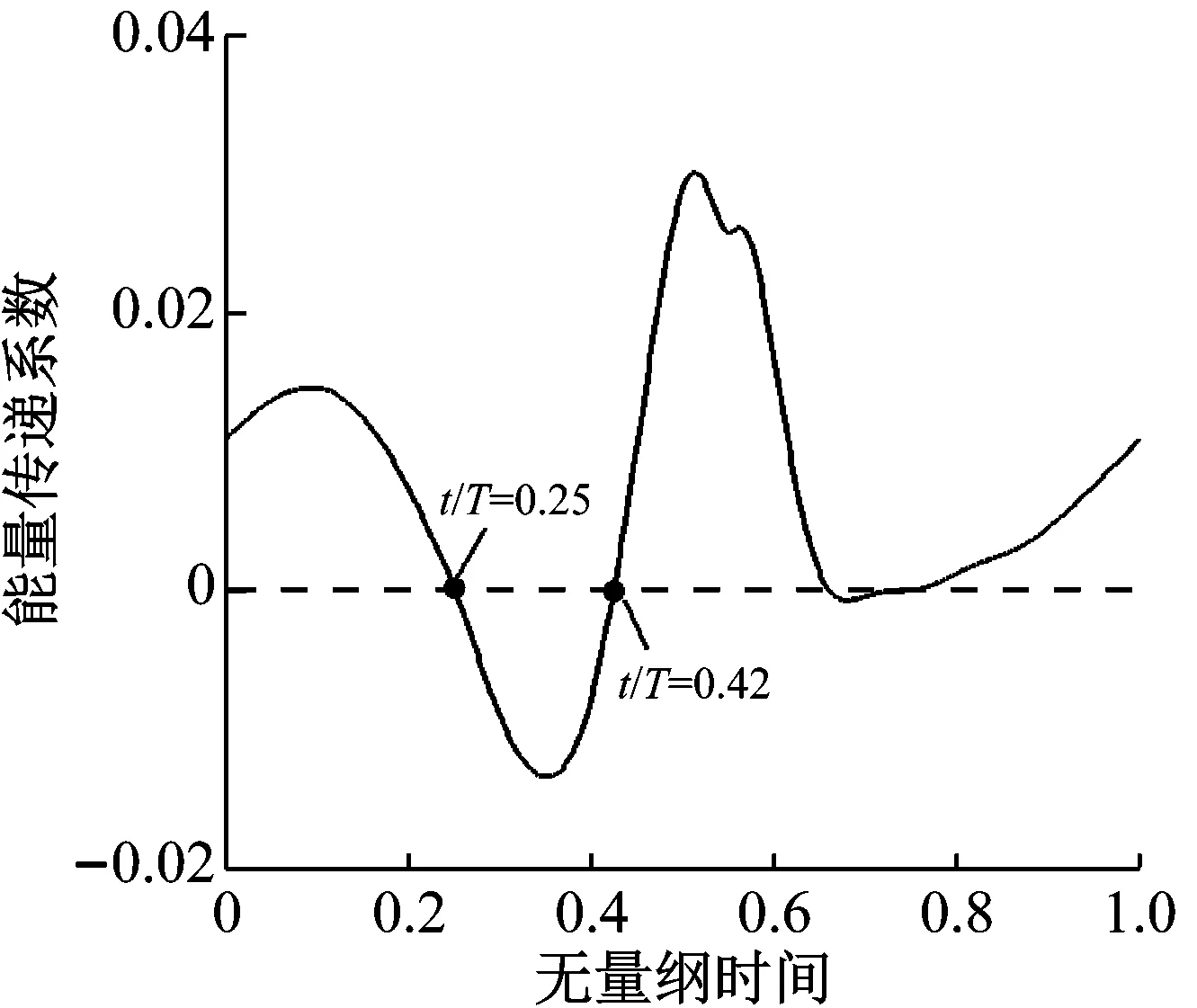
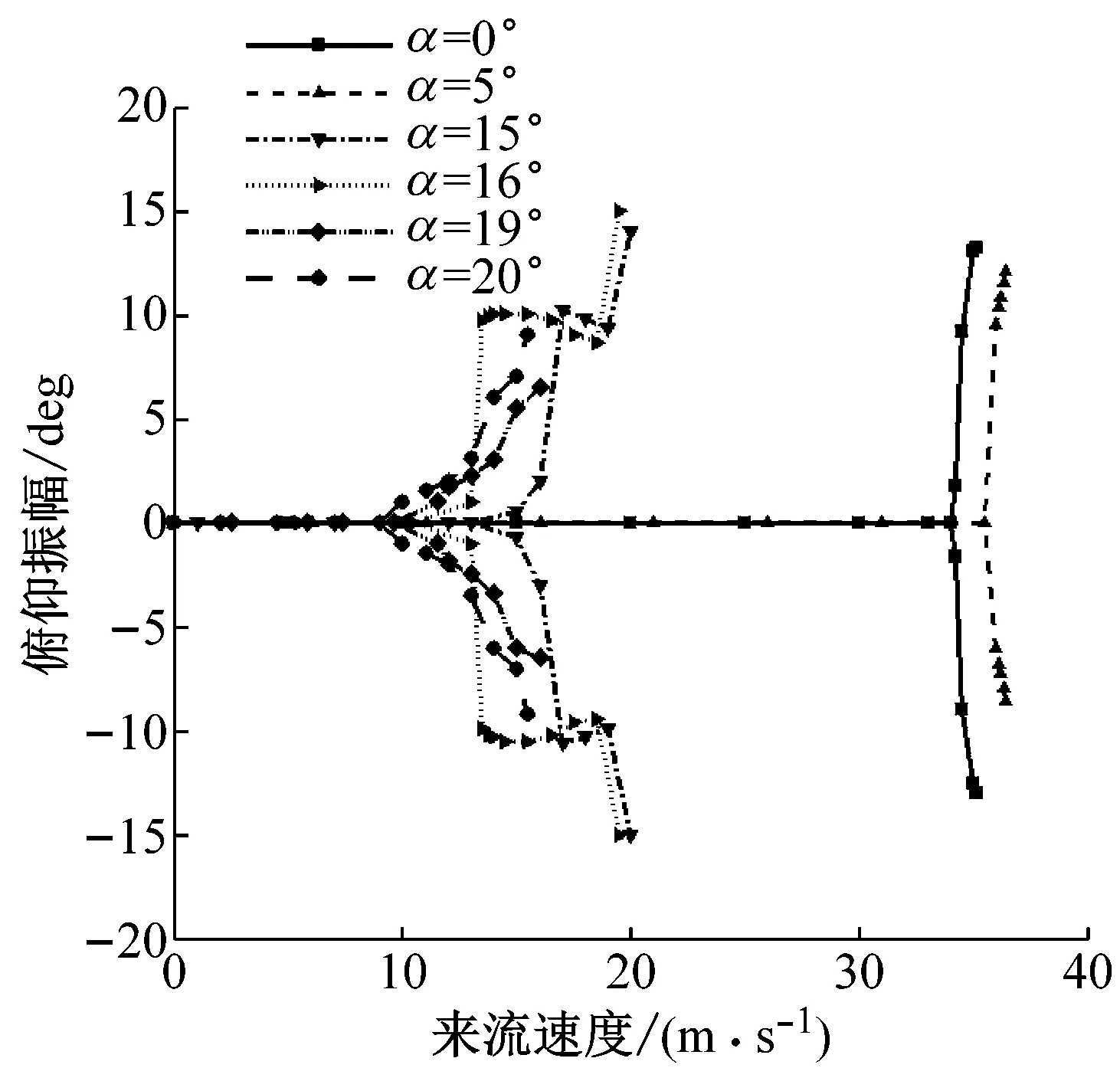
(1)前缘漩涡产生阶段(0 当翼型正向(上仰)转动时,即图13(a)~(c),翼型前缘处开始产生漩涡并逐渐扩大。从图14(a)中可知,翼型上表面的摩阻系数分布在t/T=0和0.125时几乎没有小于零的区域,意味着此时翼型上表面几乎不存在分离流动;当t/T=0.25时,翼型前缘处的摩阻系数分布小于零,即出现分离流动,此时翼型前缘处的负压增大。 (a)t/T=0 (b)t/T=0.125 (c)t/T=0.25 (d)t/T=0.375 (e)t/T=0.5 (f)t/T=0.625 (g)t/T=0.75 (h)t/T=0.875 (a)前缘漩涡产生阶段 (b)漩涡向后移动阶段 (c)漩涡逐渐脱落阶段 (2)漩涡向后移动阶段(0.25 当翼型到达正向最大位移处开始负向(下俯)转动时,即图13(c)和(d),结合图14(b)可知,翼型上表面的摩阻系数分布在t/T=0.25、0.3、0.35和0.4四个不同时刻均出现小于零的区域,并且该区域向后缘移动,这意味着翼型上表面的漩涡开始向后缘移动。 (3)漩涡逐渐脱落阶段(0.4 当翼型接近初始平衡位置并继续转动时,即图13(e)~(h),结合图14(c)可知,翼型上表面的摩阻系数分布随着翼型的不断运动,其小于零的区域逐渐减小,这意味着位于翼型上表面的漩涡开始逐渐脱离翼型表面。 图15展示了一个周期内翼型的俯仰力矩系数和压力中心位置变化情况,其中Xcp为压力中心沿翼型弦向的坐标,横向虚线为旋转轴位置。 图15 一个周期内俯仰力矩系数和压力中心变化曲线Fig.15 Moment coefficient and pressure center curve in a whole motion period 图16 一个周期内的瞬时能量传递系数Fig.16 The instantaneous energy transfer coefficient in a whole motion period 失速颤振除了伴随着分离流动外,由于其流动的特殊性和复杂性,同时还可能具有其他一些复杂现象。本小节将对该翼型在失速颤振中出现的锁频及分岔现象进行分析研究。 该翼型的分岔图如图17所示,分别展示了初始攻角为0°、5°、15°、16°、19°、20°时在不同自由来流速度下的位移幅值。其中振幅为0的点为收敛状态,横轴为自由来流速度,纵轴为某自由度下的位移幅值。从图中可以得知,当初始攻角为0°、5°时,浮沉和俯仰振幅在来流速度超过颤振临界速度后急剧增大,出现超临界Hopf分岔;当初始攻角为15°、16°时,浮沉和俯仰振幅在来流速度超过颤振临界速度后先发生跳跃,随后出现小幅下降,接着又发生跳跃;而当初始攻角为19°、20°时,浮沉和俯仰振幅在来流速度超过颤振临界速度后持续缓慢增长。 在3.2节对翼型的颤振边界进行了验证和分析,从图17可以得知,颤振频率在初始攻角增大至15°时突然减小,随后在17°时陡增。这种特殊现象与流场和结构的耦合机制有关。图18展示了不同初始攻角和自由来流速度下的颤振频率,在自由来流速度超过颤振临界速度后,当初始攻角为0°和5°时,颤振频率随来流速度的增加而增大;当初始攻角为15°和16°时,颤振频率维持在11.3 Hz左右,接近结构的固有频率,与来流速度大小基本无关;当初始攻角为19°和20°时,颤振频率随来流速度的增加而略有减小。为了进一步分析发生锁频时结构振动频率的变化,对初始攻角为15°时的俯仰力矩系数进行快速傅立叶变换得到功率谱密度(PSD)示意图,如图19所示。图中结果表明,结构振动频率的主峰值不跟随自由来流速度的变化而变化,而是锁定在结构固有频率附近,即发生锁频。结合以上分析结果,翼型在初始攻角为15°、16°和17°时发生锁频,导致颤振频率减小。 综上所述,失速颤振中出现的分岔及锁频现象对其颤振特性有显著影响,明显有别于经典颤振,因此在失速颤振计算研究中需要特别关注。 (a)浮沉位移幅值 (b)俯仰位移幅值 图18 不同初始攻角和自由来流速度下的颤振频率对比Fig.18 Comparison of flutter frequency at different initial AOAs and freestream velocities 图19 功率谱密度(PSD)示意图(α=15°)Fig.19 Power spectrum density(PSD) (α=15°) 本文基于非定常RANS方程和结构运动方程,建立时域气动弹性分析方法,对由分离流动诱发的失速颤振和锁频现象进行了研究。结果表明: (1)本文采用的非定常RANS求解器可以准确模拟动态失速气动力响应和锁频区域。 (2)采用本文建立的时域气动弹性数值模拟方法对NACA23012翼型的颤振边界进行预测,结果表明本文预测得到的颤振速度边界和实验结果吻合较好。 (3)通过对初始攻角α=15°、自由来流速度v=17 m/s时下的结构运动响应和流动特性进行分析,发现在失速颤振中前缘漩涡的产生和尾涡脱落是一种能量转换和注入机制,用以维持翼型的等幅振荡。 (4)不同的初始攻角和来流速度导致翼型的振动特性发生分岔,而翼型在初始攻角为15°、16°和17°时发生锁频现象导致其颤振频率突然减小。







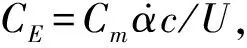

3.3 失速颤振中的锁频及分岔现象研究



4 结 论

