基于MD-CUSUM和TD-SVR的滚动轴承健康状态预测
夏均忠,吕麒鹏,陈成法,刘鲲鹏,郑建波
(陆军军事交通学院 军用车辆实验实习中心,天津 300161)
滚动轴承技术状态描述的关键是其故障特征提取,然而常用方法提取到的故障特征存在着特征空间过大,不能单调性描述轴承健康状态等问题。为了解决这些不足,需要对特征向量进行降维处理。最常用的线性降维方法有主成分分析和线性判别法[1]。由于其特征空间压缩过程具有不可控性和随机性,效果不稳定,并且对具有非线性关系的数据处理能力较差。而非线性降维方法具有更好的表现。局部线性切空间法[2]利用局部空间考虑全局因素,不可避免会损失特征性质。多维尺度法(Multidimensional Scaling,MDS)[3]利用一维空间中的目标距离反映数据之间的相似性,但其“目标距离”的计算效果一般。由此等距映射法(Isometric Feature Mapping,ISOMAP)[4]利用测地距离取代欧式距离,然后进行MDS取得了更好的效果,但是准确度不佳。累积马氏距离(Cumulative Sum and Mahalanobis Distance,MD-CUSUM)[5]与其他方法存在着本质上的区别,它充分发挥马氏距离在特征相似度检验上的优点,对特征值进行累积和(Cumulative Sum,CUSUM)检验,获得能够准确反映轴承健康状态的低维特征,并增强了其单调性。
支持向量回归(Support Vector Regression,SVR)是一种基于结构风险最小化原理,具有出色的小样本学习能力的预测模型,其常用于轴承健康状态预测[6]。当前许多学者主要对SVR参数的选择进行优化[7-9],而对于其输入与输出的相互关系没有太多考虑。本文结合轴承健康状态的时间属性,定义输入与输出之间的时间滞后(Time Delay)关系,构建时滞性支持向量回归(Time Delay Support Vector Regression,TD-SVR)模型,实现由当前状态预测未来状态的目的。
首先应用累积马氏距离(MD-CUSUM)获取反应轴承健康状态的健康指标(Health Indicator,HI),其次构建时滞性支持向量回归模型对滚动轴承健康指标进行预测,最后通过试验对比分析了MD-CUSUM方法和ISOMAP方法的优劣,论证MD-CUSUM和TD-SVR相结合的方法在轴承健康状态描述和预测方面的优越性。
1 累积马氏距离(MD-CUSUM)
马氏距离(Mahalanobis Distance,MD)是印度统计学家Mahalanobis在欧式距离基础上提出的一种方法,它可以有效地反应两个未知样本的相似度,其优点在于克服了欧氏距离存在的不足,排除变量之间的相关性干扰,具有较好的敏感性[10]。马氏距离算法步骤如下
步骤1 计算均值和标准差
(1)
(2)
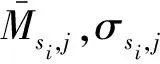
步骤2 计算相关参数
Dp×q=diji=1,2…p,j=1,2…q
(3)
式中:p为检测点数;q为特征数量;dij为第i个检测点的第j个特征值;Dp×q为特征值矩阵。
(4)
(5)
(6)
式中:cij表示距离参数。
步骤3 马氏距离计算公式
(7)
式中:Q为特征向量的协方差矩阵。
尽管马氏距离在反应数据之间的相似度方面有较好的表现,但是当数据样本之间存在着连续微小变化的情况下,很难单纯地从马氏距离上反应各数据样本的状态,因此引入累积和检验对马氏距离进行优化。
累积和(Cumulative Sum,CUSUM)检验是由英国剑桥大学Page基于似然比导出的一种控制图模型[11]。它可以通过不断累积待测值与标准值的差值,从而达到放大数据波动的目的,因此能够更加迅速、敏感地检测到微小的变化情况。其计算公式如下
(8)
(9)
S0=δ0+k
(10)

对滚动轴承振动信号数据样本的MD值进行累积和(CUSUM)检验,通过样本变化累积值表征轴承退化性能,准确反应轴承健康状态的单调性。本文选择CUSUM正向累积值作为目标参数,定义为轴承健康指标(HI)
(11)
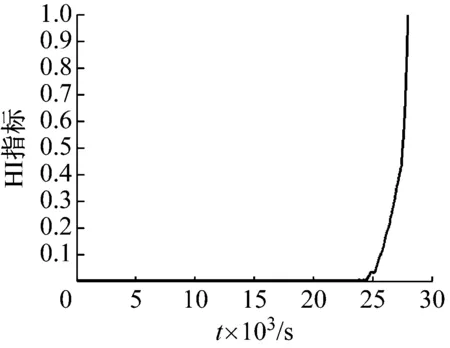
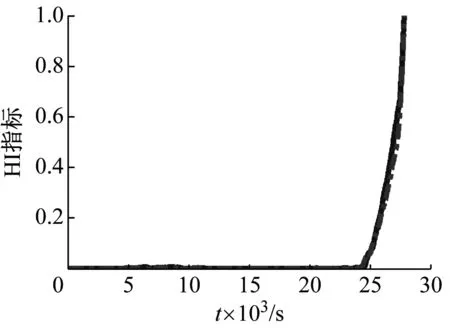
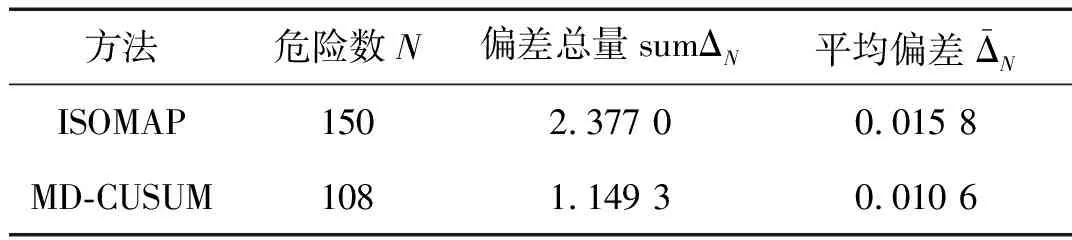
为了便于计算和分析,统一把指标进行归一化处理(式(12)),即0 (12) 式中:reg,reg′分别为需要进行归一化的原始数据和归一化之后的数据。 支持向量回归(SVR)是典型的自回归模型,是支持向量机用于解决回归问题时的推广形式[12]。支持向量回归包括线性回归和非线性回归,由于提取的滚动轴承特征具有非线性,故采用非线性支持向量回归,并对其输入和输出进行改进,得到时滞性支持向量回归。 时滞性支持向量回归(TD-SVR)就是在没有先验知识的前提下,寻找具有时滞性的输入和输出变量之间的联合分布关系,可以由一个函数表示:y=f(x)。X表示一个训练集,X={xi,xi+Δt,i=1,…l},xi是第i个训练样本,xi+Δt是第i个训练样本的目标值(即时滞Δt后的样本值),l是训练样本的容量。训练支持向量回归就是找到一个回归函数 (13) (14) 通过最小化目标函数求得 (15) 因此,时滞性支持向量回归可以简化为 (16) 基于MD-CUSUM和TD-SVR的滚动轴承健康状态预测流程,如图1所示。 图1 健康状态预测流程图Fig.1 Flowchart of predicting health state 离线阶段: (1)输入信号,进行特征提取。 (2)应用MD-CUSUM获取轴承健康指标。 (3)训练时滞性支持向量回归模型。 在线阶段: (1)采集轴承实时信号,进行特征提取。 (2)应用MD-CUSUM获取轴承当前健康指标。 (3)把当前指标输入到训练好的模型,获取轴承全寿命健康指标预测值。 定义 2.3 设{Xt;R+}是L2(Γ;η)中稠定线性算子族,对于∀R+,若存在L2(Γ;η)上稠定线性算子Yt,满足 与其他降维方法相比,MD-CUSUM不仅可以在低维空间上较好地反应轴承健康状态,而且能够识别特征之间更加微小的变化,增强了轴承健康状态在全寿命上的单调性。其次TD-SVR在支持向量回归的基础上增加时滞性,融合时间特征,更加符合轴承全寿命健康状态的预测要求。 试验验证的数据来源于PRONOSTIA实验平台[13]。其主要由驱动电机、联轴器、压力气缸、扭力计、加速度传感器、温度传感器和NI数据采集卡等组成[14]。 试验采集轴承的振动信号,两个加速度传感器(灵敏度为100 mv/g)分别位于竖直(12点钟)和水平(3点钟)方向。试验数据包括轴承的全寿命数据,即从健康状态到轴承完全损坏为止。试验轴承转速为1 800 r/min,负载为4 000 N,采样频率为25.6 kHz,采样间隔为每10 s采集0.1 s的数据即每组数据包含2 560个数据点。历时7小时47分钟,共采集2 803组数据。 小波包分解能够实现频带的均匀划分,克服了小波变换对高频信号检测精度较低的不足,由于轴承健康状态的变化在时间上相对缓慢,单一从低频部分或某一频域上很难准确反映健康状态的发展,因此具有全频域、高精度特点的小波包分解能更好地反应轴承当前技术状态[15]。对数据进行三层小波包分解,得到8个小波包。对每一时刻数据分别进行特征提取,计算每个小波包的绝对值之和,如图2所示。 图2 某一时刻小波包分解结果Fig.2 Features extracted using wavelet packet decomposition as a time point 为了便于比较分析,对各小波包能量进行归一化处理(式(12)),由此可以得到八维的向量空间,能够较为准确反应轴承的健康状态。 上述得到的特征向量维度较高,这对于反应轴承健康状态的全面性很好,但是对于健康状态的描述评价以及之后模型的训练和预测来说十分不便。因此需要对高维特征进行降维处理,得到健康指标(HI)。 为对比分析,应用等距特征映射(ISOMAP)对高维特征进行降维。等距特征映射是麻省理工学院JoshTenenbaum教授于2000年提出的算法[16]。其降维思想是对高维数据使用测地距离来代替欧式距离,得到高维数据测地距离矩阵之后再进行多维尺度(MDS)分析处理,得到高维数据从高维空间到低维空间的映射关系。应用ISOMAP把八维特征映射成一维特征,即健康指标(HI),其结果如图5所示。 图3 特征在时域上的马氏距离(MD)Fig.3 MD of features in time domain 图4 MD-CUSUM处理得到的HI指标Fig.4 HI using MD-CUSUM 图5 ISOMAP处理得到的HI指标Fig.5 HI using ISOMAP 应用时滞性支持向量回归对轴承全寿命健康状态进行预测。选取一定量的训练样本,其输入为时间t时刻的一维特征指标HIt,输出为滞后时间Δt之后的特征指标HIt+Δt,构建所需的时滞性支持向量回归(TD-SVR)模型。 对时滞性支持向量回归(TD-SVR)模型进行训练,而模型训练的准确度与支持向量回归核函数的选择息息相关。核函数的性能可以由其相应的均方根值来反应,均方根值越小表示相应核函数的性能越好,模型预测的准确度越高。通过选择不同的核函数对模型进行构建并计算其均方根值,结果见表1。 表1 不同核函数的性能Tab.1 Performance of Kernel functions 高斯径向基核函数的性能最好,构建的模型也最优。高斯模型的参数设置范围为{10-6,10-5…,1},其中参数为σ=10-5时最优。 选择Δt=20,即时滞为200 s。模型输入选择均匀分布的80个离散样本点,输出为其时滞的HI指标。应用ISOMAP、MD-CUSUM得到的HI指标分别进行TD-SVR预测,其结果如图6所示。 从图6中可以较为明显地看出MD-CUSUM的HI指标TD-SVR预测结果相比于前者的预测结果更优。 为了更加直观地比较两种方法的优劣,首先计算结果的偏差值ΔHIi,如图7所示。 (17) 应用ISOMAP的HI指标TD-SVR预测误差较大;两种方法在轴承的全寿命HI指标预测上都存在不同程度的较大误差。由图4可知,试验轴承在接近25 000 s时,产生了健康状态突变即发生了较为明显的故障,两种方法在故障发生前后对于HI指标的预测都出现较为明显的偏差和波动。 (a)应用ISOMAP的HI指标TD-SVR预测 (b)应用MD-CUSUM的HI指标TD-SVR预测 (18) 式中:l为样本数量。 maxΔ=max|ΔHIi| (19) (a)应用ISOMAP的HI指标TD-SVR预测误差 (b)应用MD-CUSUM的HI指标TD-SVR预测误差 (20) 根据式(18)、(19)、(20)和ΔHIi计算其误差指标,见表2。 表2 误差指标Tab.2 Error indicators 在平均偏差和最大偏差方面,MD-CUSUM均比ISOMAP更优,HI指标的TD-SVR预测结果更接近实际情况。 对于危险数N,当ΔHIi>0时,即预测值小于实际值时,表示轴承预测健康状态好于实际健康状态,这对于轴承运行和维护的安全性是不利的,正确的预测结果应该是保守预测,即预测的健康状态劣于实际健康状态,这样才能保证轴承运行和维护的安全性。在统计的2 783组试验数据中,ISOMAP有150个时刻的预测结果存在危险性,达到了5.390%,MD-CUSUM方法只有108个时刻,3.881%的预测存在危险性。 为了更加直观反应两种方法在预测安全性上的优劣,对危险数N进一步分析。对于存在预测危险的时刻,计算其偏差量,结果见表3。其可以反映其危险发生的概率,偏差量越大表示其发生危险的概率越大。ISOMAP在危险数和危险发生几率上都高于MD-CUSUM,体现了后者在轴承健康状态预测方面具有更高的安全性。 表3 危险数指标Tab.3 Indicators of dangerous 根据上述试验分析对比,MD-CUSUM的健康指标在轴承健康状态描述上能更好地增强其寿命单调性,描述更准确;TD-SVR模型在轴承健康状态预测上拥有更突出地表现,其结果更优。 论文首先系统研究了累积马氏距离(MD-CUSUM)的含义,得到反应轴承健康状态的低维特征健康指标(HI);其次构建时滞性支持向量回归(TD-SVR)对滚动轴承HI指标进行预测;最后通过试验验证,对比分析了ISOMAP和MD-CUSUM在轴承健康状态描述和预测方面的效果,后者具有明显的优势。 (1)MD-CUSUM克服了马氏距离在反应样本微小变化和滚动轴承健康状态单调性存在的不足,应用累积和理论增强马氏距离对变化的敏感性以及健康状态的单调性,能更准确地描述轴承健康状态。 (2)时滞性支持向量回归模型以支持向量回归为基础,建立输入和输出的时滞性关系,更好地契合了滚动轴承全寿命预测,实现由已知当前轴承健康状态预测轴承全寿命健康状态的目的。 (3)基于MD-CUSUM和TD-SVR相结合的方法能更清晰、全面反应轴承健康状态,能敏感识别出轴承健康状态突变点;在健康状态预测上能更准确地对全寿命HI指标进行预测,精度更高,安全性更好。2 时滞性支持向量回归(TD-SVR)
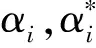
3 健康状态预测流程

4 试验验证
4.1 特征提取


4.2 健康指标获取



4.3 模型构建

4.4 结果分析
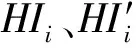




5 结 论

