一种基于DCWPSO算法与FFD模型的心脏CT序列图像配准算法
王 雷,郭 全
(山东理工大学 计算机科学与技术学院, 山东 淄博 255049)
一种基于DCWPSO算法与FFD模型的心脏CT序列图像配准算法
王 雷,郭 全
(山东理工大学 计算机科学与技术学院, 山东 淄博 255049)
为实现心脏CT图像不同序列间的自动配准,提出了综合动态调整惯性因子权重的粒子群算法(DCWPSO)和自由形变 (FFD)模型的非刚体医学图像配准方法.在对比常用的单纯形算法和模拟退火(SA)算法的基础上,采用动态调整惯性因子权重的自适应粒子群算法求解全局配准参数,克服了基于梯度的优化方法耗费时间长的缺点.在全局配准的基础上以FFD模型的形式应用层次B样条进行非刚性局部配准,利用B样条层次加细策略提高了配准的精度.实验结果表明,所提方法能够得到更好的配准结果.
心脏CT序列图像;医学图像配准; DCWPSO算法; FFD模型
当前,多排螺旋CT在扫描速度及图像清晰度等方面有了新的突破,对冠状动脉分支斑块和支架腔内的显示能力明显增强,对心房心室等腔室的形态学观察更加细致.对心脏CT序列图像配准是利用CT图像进行定量分析和手术评估的重要前提,它广泛应用于心血管疾病的计算机辅助诊断以及手术方案的规划及评估等领域[1].因此,研究心脏CT序列图像配准对于提高心脏疾病的诊断效率具有重要的现实意义.然而,心脏是典型的运动器官,其形态随呼吸运动而周期性变化.传统的简单刚体配准无法描述心脏CT图像中复杂而不规则的形变场,而现有的非刚性配准算法存在难以自动选择初始值的缺点.针对上述问题,本文提出一种自动的非刚性配准方法.
1 心脏CT序列图像配准算法过程
图像配准的本质是求解待配准图像的最优空间变换,其表现形式是光滑的形变场[2].不同序列的心脏CT图像的几何畸变分为线性和非线性畸变,前者可以用一个线性模型来描述;而呼吸运动导致的心脏局部畸变需要一个非线性模型来描述[3].令R表示参考图像,F表示浮动图像,为了准确描述序列图像间的不规则形变场,定义如下形式的变换T:
T(x,y)=Tglobal(x,y)+Tlocal(x,y)
式中:Tglobal(x,y)表示全局变换,用来描述心脏CT图像的线性几何畸变;Tlocal(x,y)代表局部形变,用于描述心脏CT图像的非线性几何畸变.本文所提出的配准算法过程如图1所示.

图1 本文所用配准算法流程图Fig.1 The flow chart of the proposed registration algorithm
1.1 基于DCWPSO算法的全局变换模型
1.1.1 全局变换模型
为了描述心脏CT序列图像间的简单刚体变换并降低计算复杂度,选用仿射变换[4]作为全局变换模型,用6个参数描述心脏CT序列图像间的线性形变,即
式中:e11=kcosθ,e12=ksinθ,e13=tx,e21=-ksinθ,e22=kcosθ,e23=ty;k表示缩放比例因子,θ表示旋转角度,tx,ty分别表示x方向和y方向的位移.
1.1.2 基于DCWPSO算法的优化策略
为了求解上述6个变换参数,采用动态调整惯性因子权重的自适应粒子群算法[5-6],相比传统的粒子群算法,它通过进化速度因子h和聚集度因子s动态地调整惯性因子权重以达到更新粒子飞行速度和位置的目的,避免优化过程陷入局部极值,从而得到更加准确的全局最优解.记第i个粒子的位置为xi,i=1,2,…,m;粒子当前已经到过的最好位置记为pbest,整个种群到过的最好位置记为gbest.算法具体过程如图2所示.
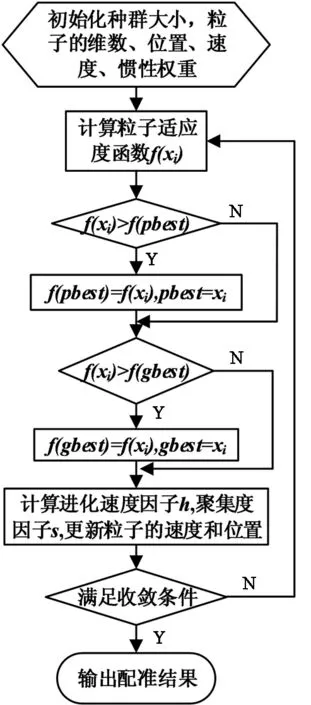
图2 DCWPSO算法流程图Fig.2 The flow chart of the DCWPSO algorithm
1.2 基于层次B样条的FFD局部变换模型
1.2.1 FFD局部层次变换模型
令Ω={(x,y)|0≤x 式中,0≤u<1. 设Φ0,Φ1,Φ2,…,ΦK表示K+1层控制网格,假设从k至k+1层控制顶点依次递增,那么FFD模型就可以写成多层子模型[8]组合的形式 1.2.2 基于标识点的MBA算法 为了在两幅图像上自动选取标识点,本文使用一种基于区域相似性自动寻找标识点的方法,即:对于参考图像R中的每一个标识点pi,构建以pi为中心的m×n的窗口Wr,在浮动图像对应位置u×v搜索窗口Wf,当Wf与Wr在某种目标函数下达到最优值时,窗口Wf的中心qi即为pi对应的标识点. 当获取标识点后,在每一层网格调用B样条近似(B-Spine Approximation, BA)算法,求得控制顶点,得到每一层的形变函数Tklocal(x,y),在所有的层次调用BA算法的过程称为多层次BA算法(MBA),得到最终的形变函数Tlocal(x,y),然后将它作用于浮动图像,重采样就得到配准后的图像,具体过程如图3所示. 图3 MBA算法流程图 Fig.3 The flow chart of the MBA algorithm 本文所用算法平台使用VC++语言编写,其界面如图4所示.为了验证本文所用算法的准确性,选取了不同序列的心脏CT图像作为实验对象,图像的大小为256×256. 图4 本文所用算法平台界面 Fig.4 The platform interface of the proposed algorithm 由于现在还没有一个统一的“金标准”用于图像配准结果的评价,因此本文通过比较配准前后图像的互信息和相关系数来评价配准结果的有效性和准确性[9]. 表1和表2是3种配准方法的量化结果.实验表明,对于DCWPSO算法的进化速度因子和聚集度因子在惯性因子权重中所占的比例,wh取值0.6,ws取值0.1效果较好,惯性因子权重初值为0.9.在本次实验中,通过表1和表2可知,3种方法配准后互信息和相关系数都变大,从综合配准时间和精度来看,粒子群算法要优于其他两种方法. 表1 三种优化方法得到的配准参数 表2 全局变换配准前后结果对比 方法互信息相关系数配准前配准后配准前配准后单纯形0.390.490.320.40SA0.390.480.320.41DCWPSO0.390.510.320.44 本文实验使用8×8的网格,网格层数为3.多层优化方法比单层模型迭代次数更多,时间消耗略有升高.单层和多层模型形变产生的网格如图5所示. (a)单层模型 (b)多层模型图5 局部FFD模型的配准结果及形变网格Fig.5 The registration result of the local FFD model and the deformation grid 表3 局部FFD模型配准前后结果对比 方法互信息相关系数前后前后时间/ms单层FFD0.390.480.320.4114230多层FFD0.390.560.320.4219853梯度方法0.390.600.320.4575416 由表3可知,对于FFD模型使用层次优化策略,配准后的互信息和相关系数明显高于单层的结果,配准精度提高.对比图5 (a)和图5(b)可知,多层模型形变的光滑性比单层模型效果更好,而基于梯度搜索策略求解控制点的配准方法配准的时间相比较而言太长,不能满足实际应用的要求. 本文所提出的配准方法过程分为两步执行,配准时间略有提高是可以预见的.图6是本文所用算法得到的形变网格. 图6 本文算法配准得到的形变网格Fig.6 The deformation grid of the proposed registration algorithm 通过对比表2、表3以及表4中的数据可知,使用本文方法配准后互信息和相关系数比单一使用全局变换或者局部FFD模型后的值更大,这表明配准精度进一步提高,而配准的时间也在可以接受的范围内.从所产生的形变场网格来看,本文方法产生的形变网格光滑性最好.综合考虑上述因素可知,本文所提配准方法取得了更好的效果. 表4 本文算法配准前后结果对比 方法互信息相关系数前后前后时间/ms单纯形+FFD0.390.570.320.4230269SA+FFD0.390.580.320.4633604DCWPSO+FFD0.390.690.320.5529805 针对心脏这种运动器官的CT序列图像配准问题,本文提出了综合DCWPSO算法和FFD模型的非刚性配准方法,并且采用B样条层次优化策略提高了配准精度.下一步将采用多分辨率优化策略,寻找更准确的最优解,进一步提高配准精度,并缩短配准时间,以利于实际的临床诊断. [1]杨素君, 郑园园, 楚坤义,等. 国内冠状动脉心脏CT研究新进展[J].中西医结合心脑血管病杂志,2014,12(11):1 380-1 382. [2] SOTIRAS A, DAVATZIKOS C, PARAGIOS N. Deformable medical image registration: a survey[J]. IEEE Transactions on Medical Imaging, 2013, 32(7): 1 153-1 190. [3]蔡肯. 基于双源CT的全心脏图像配准与自动分割算法研究[D]. 广州: 华南理工大学, 2013. [4] 赵海峰,陆明,卜令斌,等.基于特征点Rényi互信息的医学图像配准[J]. 计算机学报,2015,38(6):1 212-1 221. [5] 张良安, 万俊, 谭玉良. 基于改进混沌粒子群算法的 Ahut-Delta并联机构尺度综合[J]. 农业机械学报,2015,46(8):344-351. [6] 冯林,张名举,贺明峰.用改进的粒子群算法实现多模态刚性医学图像的配准[J].计算机辅助设计与图形学报, 2004,16 (9):1 269-1 274. [7] MATTIAS P H, IVOR J A S, BARTLOMIEJ W P,et al. Deformable image registration by combining uncertainty estimates from supervoxel belief propagation[J].Medical Image Analysis, 2016,27:57-71. [8] 徐丽燕, 陈允杰, 邱军,等. 基于B样条的云图非刚性配准方法[J]. 测绘学报, 2011, 40(3):326-331. [9] SMISTAD E, FALCH T L, BOZORGI M, et al. Medical image segmentation on GPUs-A comprehensive review[J].Medical Image Analysis,2015,20(1):1-18. SequencedcardiacCTimageregistrationbasedonDCWPSOalgorithmandFFDmodel WANG Lei, GUO Quan (School of Computer Science and Technology, Shandong University of Technology, Zibo 255049, China) In order to realize the automatic registration for the sequenced cardiac CT image, a registration method based on the adaptive particle swarm optimization algorithm with dynamically changing inertia weight (DCWPSO) and free-form deformation (FFD) model is proposed. By comparing simplex algorithm and simulated annealing algorithm, the DCWPSO algorithm is employed to calculate the deformation parameters of the global registration, which overcomes the disadvantage of the time loss when using the gradient-based optimization methods. Based on the global registration, the FFD model with the form of B-spline is applied for the local non-rigid registration, and the precision and accuracy improve with the help of the refined scheme for the hierarchical B-spline. Experiments demonstrate that better registration results can be obtained by the proposed method. cardiac sequenced CT image; medical image registration; DCWPSO algorithm; FFD model 2017-03-02 国家自然科学基金青年科学基金项目(61502282);山东省自然科学基金青年科学基金项目(ZR2015FQ005);山东理工大学博士科研启动经费资助项目(414023) 王雷,男,wanglei0511@sdut.edu.cn. 1672-6197(2018)01-0001-04 TP391.41 A (编辑:郝秀清)

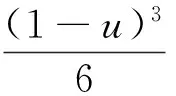

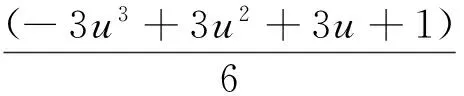
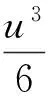

2 实验结果及分析
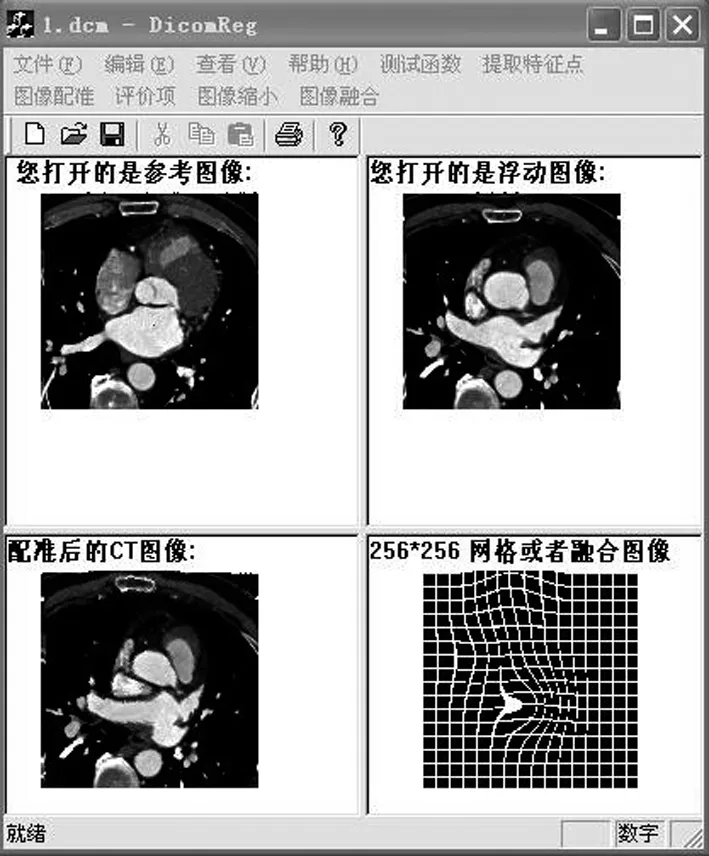
2.1 全局变换配准结果
Tab.1 The registration parameters obtained by the three optimization methods
Tab.2 The comparison before and after registration using the global transformation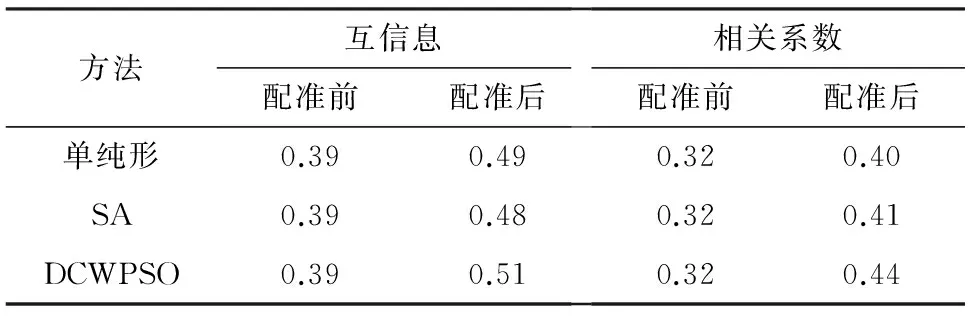
2.2 局部FFD层次模型配准结果

Tab.3 The comparison before and after registration using the local FFD model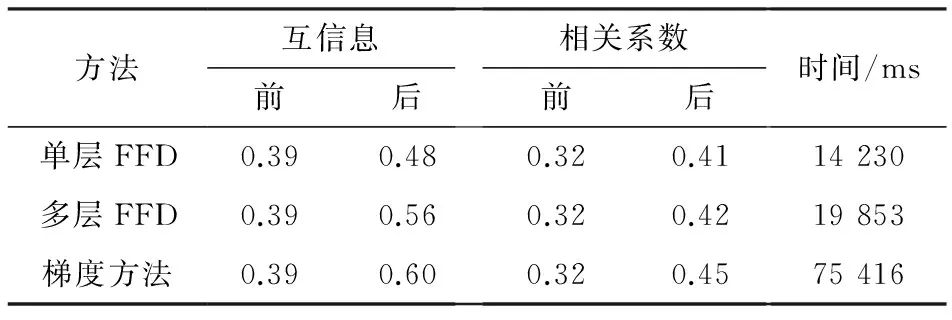
2.3 本文算法的配准结果

Tab.4 The comparison before and after registration using the proposed algorithm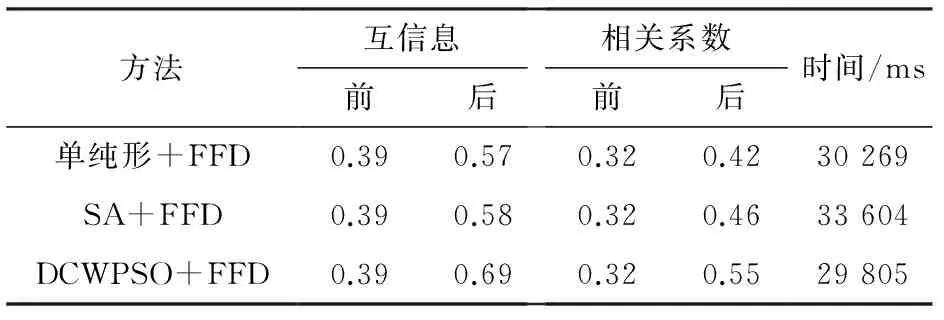
3 结束语

