基于离散元模拟筒仓贮料卸料成拱过程及筒仓壁压力分布

刘克瑾，肖昭然，王世豪



基于离散元模拟筒仓贮料卸料成拱过程及筒仓壁压力分布

刘克瑾，肖昭然，王世豪

（河南工业大学土木建筑学院，郑州 450001）

筒仓卸料时贮料作用在仓壁上的卸料压力出现骤然增大以及震荡分布的现象，该文从贮料的散体颗粒性入手，采用离散元法和模型试验法研究贮料在静止储粮状态和卸料过程中的力学行为，从细观颗粒层次探求卸料时贮料内部土拱效应与宏观仓壁卸料压力增大及产生震荡的本质联系。模型为平底立筒仓，高1.0 m，宽0.5 m，卸料口直径0.1 m，数值模型填充20 400个球形单元，模型试验贮料为大豆。首先，通过分析卸料中仓底压力分布的周期性变化规律，证实了卸料口附近拱效应的存在。然后选取结拱起始、结拱完成及拱塌落3个时间点仓内贮料的力链网络、竖向应力、横向应力、主应力方向和速度场分布，分析了卸料时的拱效应及其对仓壁卸料压力分布的影响。研究发现，卸料中，筒仓底部的卸料口附近有拱形成，其跨度为卸料口直径的4.0倍，高度为卸料口直径的2.5倍。随着物料的流出，卸料口附近的颗粒物质遵循“拱形成-拱塌落”的动态规律，并据此提出了筒仓卸料的动态成拱机制。深高比0.35处，动态压力修正系数最大为2.70。在深高比0.85处，结拱完成时的仓壁压力达到峰值3.57 kPa。分析结果表明，拱的形成是仓壁压力增大的根本原因，动态成拱机制则是宏观仓壁压力产生震荡的根本原因，仓壁压力峰值作用点和最大动态压力修正系数作用点并不一致。动态成拱机制以及由此引发的仓壁卸料压力分布规律，可为构建机理研究的筒仓结构安全设计提供参考。

应力；数值方法；筒仓；仓壁压力；拱；大豆；颗粒物质；细观研究

0 引 言

一定数量的颗粒聚集体具有复杂的力学特性，传统的固体力学理论、流体力学理论和凝聚态物理很难对其做出准确的解释。筒仓作为贮存颗粒物质的主要载体，其受力特性十分复杂。研究表明，筒仓散体物料的卸料过程中，仓壁受到的卸料压力峰值可以达到静态压力的数倍[1-4]，大部分筒仓工程事故都是由这种过大的卸料压力引起的。近年来，学者们对此进行了探索并取得了初步的共识，即卸料过程中出现在卸料口附近的拱效应是仓壁压力增大的主要原因[5-7]。对于拱效应的研究，由于传统测量方法的局限性，室内试验仅能得到筒仓侧壁及底部的边界受力，对筒仓内部散体颗粒体的受力特性不能进行很好的观测分析，因此也就无法直观的观察并量测到拱效应。而近年来发展的先进试验方法如静态光弹试验（孙其诚等[8]）通过量测静态堆积状态下的颗粒间接触力分布，发现了静态堆积颗粒底部存在应力凹陷现象，证明了拱效应的存在。因卸料时颗粒物质体系处于运动状态，属于大变形问题，由于等倾线的获得需要进行多次重复试验，动态光弹应力的定量分析及卸料的可重复性及精确性还有待提高[9]，不能对整个卸料过程进行精确分析。传统的室内试验无法解决的问题，从数值方法进行探索是一条新思路。

当前，数值方法中的有限元法和离散元法在模拟筒仓物料力学性能方面获得了广泛的应用。尤其是离散元法，基于作用在颗粒体上的受力分析来确定单个颗粒体的运动行为，颗粒的运动遵循牛顿第二定律。与有限元法将颗粒集合体简化为连续介质不同，离散元法对问题的模拟是基于颗粒尺度（particle-level），可以从本质上揭示颗粒集合体的宏观力学行为。此外，离散元法还可以无损的观察贮料内部受力特性和流动规律，弥补模型试验的不足。

学者们在用离散元法模拟筒仓的贮料和卸料过程，进行了初步的探索，取得了有益的成果，然而也存在需要改进的地方。这些研究多停留在宏观的唯象学描述，并没有充分发挥离散元法从细观颗粒层次研究颗粒物质力学行为的优势[10-13]。例如国内学者们观察到卸料中仓壁压力出现“震荡”变化，提出这一现象与“拱”效应相关，然而其研究局限于现象的表述，并没有深入的探讨二者的本质关系。再者，尽管有学者提出了拱效应[14-17]，也推导了拱的形态与仓壁压力的公式，然而这些推导均是基于连续介质力学，并没有从颗粒间的受力和传力角度进行分析，因而也没有从本质上揭示物料的宏观力学表现。

鉴于此，本文采用离散元方法模拟筒仓贮料及中心卸料工况，借鉴颗粒物质力学的基本理论，通过系统分析贮料的力链网络分布、竖向应力和横向应力分布、仓底和仓壁的卸料压力分布，流速分布，主应力方向分布，从细观颗粒层次探讨卸料中的拱效应原理，包括拱的起始、形成和塌落，进一步研究细观的拱效应如何影响宏观的仓壁卸料压力分布。最终从本质上揭示贮料的宏观力学行为。

1 模型建立

采用颗粒离散元软件PFC模拟贮料及中心卸料工况，并制作了相同尺寸筒仓模型的室内贮料及卸料试验。模型筒仓高1 m，直径0.5 m，卸料口直径0.1 m，位于筒仓底部中心，模型缩放比为1:20。仓体底部测墙长度为0.05 m，从左到右编号依次为1～8。仓体左右两侧各设置仓壁压力监测墙10个，测墙高度均为0.1m，其中左侧测墙沿高度方向从下到上编号依次为11～19；右侧测墙沿高度方向从下到上编号依次为21～29。室内模型试验中，筒仓形状为圆柱形，内径0.5 m，高1 m，沿仓壁两侧母线对称布置压力计，每侧6个共计12个（图1b），测量仓壁压力。试验采用DYB-3型电阻应变式压力计，其量程为20 kPa，分辨率≤0.083% F.S，综合误差＜0.8% F.S，数据采集仪采用DH5922动态应变分析测试系统。共进行了5次平行试验，每次试验取左右两侧压力计均值，文中给出的贮料压力及卸料压力为5次试验值的均值。模型筒仓及室内试验模型如图1所示。

注：1~8，11~30表示测墙编号，下同。

本文模拟的贮料为豆类等似球形散粒体，采用圆球单元，参考前人对大豆籽粒的弹性模量研究成果[18]，设置颗粒的刚度参数（表1）。依据大豆与仓壁材料摩擦系数研究成果[19]，设定墙摩擦系数为0.4，该系数可以代表墙体材料为钢板或混凝土。大豆的内摩擦角依据大豆内摩擦角研究成果[20]，综合考虑各项影响因素，选为32°，对应颗粒的摩擦系数为0.6。大豆颗粒密度与顶部压力有关，本文中，经Janssen公式计算大豆的顶部压力分布为0～1.80 kPa，参考大豆堆压缩密度与体变模量研究成果[21]设置球形颗粒单元的颗粒密度为718 kg/m3，具体颗粒单元参数示于表1。

表1 筒仓离散元法模型材料参数

2 贮料工况分析

数值模型中，仓内贮料采用点源法生成，当颗粒全部下落完成后，测墙输出仓壁及仓底的压力曲线呈水平直线时认为模型达到平衡状态，定义为贮料工况，此时模型仓中颗粒共计20 400个。室内试验模型中，满仓后静置1 h，土压力盒读数稳定，定义为贮料工况。贮料工况下的仓壁压力分布与Janssen公式[22]计算值对比如图2所示。本文中，深高比为贮料深度与筒仓高度之比。

图2 仓壁侧压力模拟值、Jassen解和试验值

图2显示数值模拟结果、试验结果与工程界普遍认可的Janssen公式计算值有较好的一致性。以试验值为参考值，模拟值和Jassen值与试验值的最大误差不超0.04和0.09，证明了离散元法的可靠性。为了观察贮料工况下颗粒接触力的分布情况，用PFC软件输出贮料工况下仓内颗粒物质的力链分布、孔隙率分布、竖向应力分布和横向应力分布，如图3所示。

图3a中，颗粒间接触力由线段表示，线段越粗，表示颗粒间接触力越大，力链强度越大。由图3a可以看出，贮料工况下，筒仓下部力链强度大且分布较为密集，相互链接形成架拱[23]。筒仓上部力链强度小且分布较为稀疏。筒仓底部，力链形成由实线标注的以及其他大小不一的弧形拱状结构，这与房营光等[24]发现的试验现象一致，仓底接触部分力链在水平方向上分布的不均匀性是压力凹陷[8]的主要原因。由图3b可以看出，由于填料时物料的随机排布特性，筒仓内的孔隙率分布并不均匀，存在类似虚线标注区域等孔隙率极小的颗粒块体。图3c中，竖向应力在竖直方向上由上到下逐渐增大，在同一高度，竖向应力在水平方向上的分布并不均匀，这种分布在筒仓中上部尤为明显。图3d中，横向应力沿竖直方向由上到下非线性增大。

图3 贮料静工况颗粒物质的力链网络、孔隙率、竖向应力和横向应力分布

对比图3a和3b发现，在颗粒块体内部，力链强度较弱且分布密集。弱力链在整个筒仓内都有分布，而强力链主要分布在孔隙率较小的区域。对比图3a、3b和3c发现，在竖向应力较大的区域内，强度较大的力链方向与重力方向夹角较小；在横向应力较大的区域内，强度较大的力链方向与重力方向夹角较大。说明强度较大的力链的方向影响区域内竖向应力及横向应力的分布。

3 卸料过程

在分析卸料过程之前，参考已有研究结论[13-14,16]：贮料卸料流动时的结拱－破拱引发了筒仓卸料时仓壁侧压力不断的上下波动，拱效应位于卸料口附近。本文尝试观察仓底压力的分布，预判是否存在拱效应。若不存在拱效应，则卸料中仓底压力分布可能是单调增大、不变或减小；若存在拱效应，即卸料口附近有拱的形成和塌落，那么拱的形成会使位于拱脚部分的仓底压力增大，拱脚两侧的仓底压力则会减小。

3.1 仓底压力分析

自卸料开始，记录各个测墙的压力变化，仓底测墙编号及位置见图4，其中1、2、7、8号测墙远离卸料口，3、4、5、6号测墙靠近卸料口。

图4 拱脚位置

研究拱效应时，考虑到颗粒物质生成的随机性，历次结拱的拱脚位置可能会有差别，因此，需进行多次模拟取统计学分析结果。本文计算时做了5次数值模拟。仓底压力的谷值和和峰值变化趋势以及仓底的压力分布基本一致，误差不超过均值的5%。分析后发现结拱的拱脚位置均处于1、2号和7、8号测墙，限于篇幅此处选取有代表性的仓底压力分布图5进行分析。

图5为卸料初期，且卸料口附近颗粒速度稳定时，作用在仓底上的卸料压力分布图。由图5可知：

1）卸料过程中仓底及仓壁的压力一直处于震荡变化状态，这一现象与文献[13,25-26]的研究相符。靠近卸料口的仓底压力较小，5号测墙仓底压力与仓底峰值压力之比不超过0.41，4号测墙不超过0.39。远离卸料口仓底压力较大，如1、2号和7、8号测墙，仓底压力与仓底峰值压力之比在0.5与1.0之间周期性变化。

2）仓底的压力变化具有一定的周期性。这一现象证明了卸料口附近拱效应的存在。尤其是1、2号和7、8号周期性压力变化明显，且其承担的压力值较大。根据拱的存在会使拱脚部分的仓底压力增大这一物理现象，进行了5次数值模拟，进行统计分析后发现，1、2号和7、8号是拱脚的位置。

3）研究拱效应的节点选择。研究表明，拱的形成会使局部（拱脚部分）仓底压力增大，拱的塌落会使局部仓底压力减小[27-28]。以此为依据：在压力始终较大且随时间变化明显的1、2号和7、8号底墙的压力变化曲线上，选取极小值点A作为结拱的起始点，选取极大值点B作为结拱的完成点，选取B点之后迅速减小后的一点C作为拱塌落的代表点。在此基础上，分别研究对应点A、B和C时刻的筒仓内部力链网络分布，竖向应力分布，横向应力分布及颗粒速度分布，并据此从细观颗粒层次分析拱的形成－塌落机理及其对仓内贮料应力分布的影响。

注：A、B、C分别为结拱起始点、结拱完成点和拱塌落点

3.2 细观颗粒层次的拱效应分析

3.2.1 结拱起始

图6a为结拱起始时刻点A的贮料力链图，图6b为竖向应力分布，图6c为横向应力（也即仓壁压力）分布，图6d为颗粒速度。

根据力链稀疏程度、力的传力角度、力链强弱、流速不同，可以将仓内颗粒体系划分为4个区域见图6a中区域1，区域2，区域3，区域4，观察图6可知：

1）区域1和4内的力链较为稀疏，且区域1内的长度较大的力链方向与竖向夹角较大；强力链主要分布在区域2和3内。相应的区域1和4内竖向应力和横向应力均较小，区域2和3内有较大的竖向应力和横向应力分布。

2）图6d显示，区域4内的颗粒流速较其他区域更大，区域3顶部以上的颗粒流动直径约为筒仓直径的3/4，在区域2和3底部附近，越靠近仓底，流动半径越小，即贮料的流态为漏斗流。

分析可知：在强度较大的力链分布的区域内，竖向应力或横向应力较大，这是因为应力的分布是由区域内力链强度决定的。对比图6b、6c和6d发现，横向应力的分布与区域内颗粒速度无明显联系；而在竖向应力较大的区域内，颗粒速度较小，反之亦然，说明区域内颗粒速度主要由竖向应力的分布决定。

注：区域1、2、3、4分别表示力链稀疏区、力链密集区、成拱区和快速流动区。

3.2.2 结拱完成

图7为结拱完成时刻点B的贮料力链图，竖向应力分布图，横向应力分布图及颗粒速度图。

观察图7可以发现：

1）区域1和2中均有强力链分布，仓壁附近力链以竖向为主，区域3中有力链呈拱形分布，区域4中力链强度较弱，且分布稀疏。相应的，区域1和2中均有较大的竖向应力和横向应力分布，较大的竖向应力主要集中分布在仓壁及区域2底部附近；区域3内有较大的竖向应力和横向应力呈拱形分布，符合拱的受力特性。

2）图7d显示，区域1内颗粒速度很小，顶部的颗粒速度为0，停止了流动，正是由于拱的形成使得拱的形成区域3及其上方流动区域的颗粒运动速度减小。

对比图7a、7b、7c和7d发现，区域1内强度较大的力链主要影响横向应力的大小及其分布，区域2内强度较大的力链主要影响竖向应力的大小及其分布，说明区域1内强度较大的力链方向以横向为主，而区域2内强度较大的力链方向以竖向为主。区域3内形成了跨度约为卸料口直径4倍，高度约为卸料口直径2.5倍的拱结构。区域4位于拱圈以下，该区遍布弱力链，竖向应力及横向应力接近零，相应的该区颗粒的流动速度也最大。

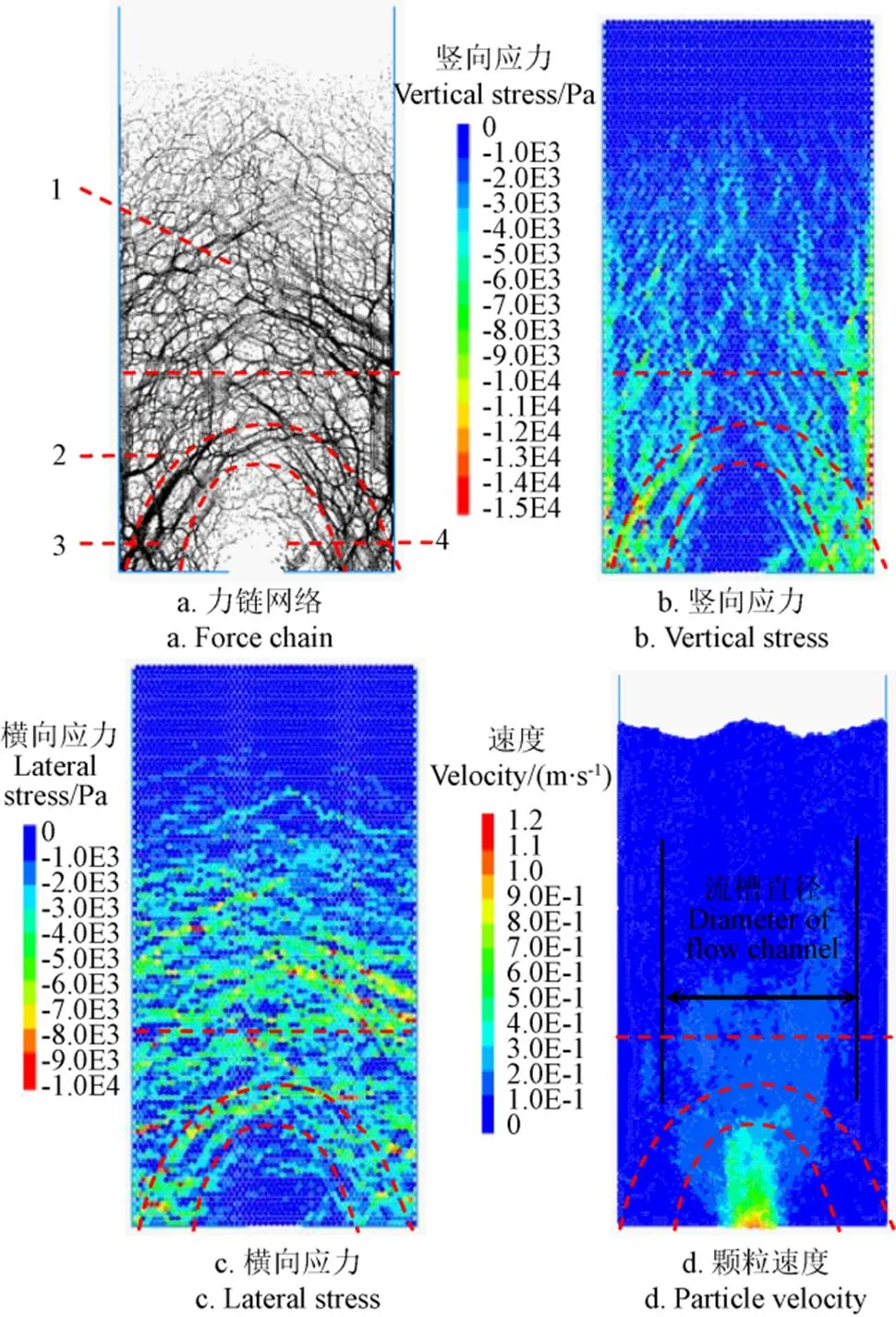
图7 结拱完成时颗粒物质的力链网络、竖向应力、横向应力和速度分布

从图6结拱开始到图7结拱完成，拱的形成主要来自于区域3内力链强度由小到大的变化。由于区域3内拱的形成，阻碍了区域2和区域1内颗粒的流动（直观表现是区域1和区域2内颗粒速度大幅度减小），区域1和2内的竖向应力和横向应力均有明显增加，且横向应力增加趋势更为明显，此时，横向应力向两侧传递作用在筒仓侧壁的横向压应力必然也会增大，由此证明了拱的形成导致卸料压力增大。该结论与已发表的土力学中的拱效应研究成果[28]相容。

3.2.3 拱塌落

图8为拱塌落时刻点C的贮料力链网络分布图，竖向应力分布图，横向应力分布图及颗粒速度图。

图8a和8b显示，强度较大的力链及竖向应力主要分布于区域1中下部、区域2仓壁附近以及区域3底部。图8c显示，区域内中下部横向应力较大，区域2内横向应力次之，而区域3和4内横向应力接近于0。图8d显示，区域4内的颗粒速度较其他区域更大。

由图7结拱完成到图8拱塌落，贮料颗粒体系的力链强度由大变小，区域2和3内的力链强度减小尤为明显。区域1、2和3内的竖向应力和横向应力也有较大程度的减小，说明拱处于塌落状态。以此可以得出，拱塌落时刻点C的仓壁压力小于结拱完成时刻点B的仓壁压力。

图8 拱塌落时颗粒物质的力链网络、竖向应力、横向应力和速度分布

3.3 主应力方向分析

PFC采用Christoffersen[29]和Fortin[30]提出的颗粒间接触力计算范围内应力的方法计算一个圆形区域内的应力张量，为更精确的判断拱的形成对仓内应力分布的影响，并借鉴赖汉江等[31]研究成果，本文将筒仓划分为200个大小相同的正方形区域，每个区域内均布置有内切于正方形的圆形测量圆，横向应力σ、切向应力σ及竖向应力σ由测量圆测定，并通过式（3）求得主应力及绝对值最大的主应力方向。将贮料工况及结拱起始时刻点A，结拱完成时刻点B和拱塌落时刻点C的筒仓内绝对值最大主应力方向（以下简称主应力方向）分布示于图9。

图9 不同时刻主应力方向分布图

图9a显示，贮料工况下主应力方向以竖向为主，且除筒仓顶部主应力方向较杂乱外，其他区域内主应力方向分布有较好的规律性：距仓壁越近，主应力方向与重力方向夹角越大。图9b显示，结拱起始时刻，筒仓下部侧壁附近主应力方向以竖向为主，但其他区域内的主应力方向较贮料工况发生了较大偏转。图9c显示，结拱完成时刻，在悬链线处形成了弧形拱状结构，拱下方的主应力方向分布较为杂乱，在拱顶的正上方，由于拱的形成阻碍了上方颗粒的流动，对上方颗粒起到了支撑作用，拱顶上方的主应力方向以竖向为主。图9d拱塌落时刻，除筒仓下部侧壁附近主应力方向以竖向为主，有着较好的规律性外，其他区域内主应力方向分布较为杂乱。

对比图9b、9c和9d发现，虽然图9b和9d中悬链线内部主应力方向有拱形分布，但其附近的主应力方向分布较为杂乱，说明悬链线附近没有拱的形成，而图9c中悬链线附近的主应力方向分布较图9b和9d有更好的规律性，说明悬链线附近有拱的形成。在拱的形成过程中，由于拱对上方颗粒的支撑作用，拱顶上方的主应力方向与重力方向的夹角减小；在拱的塌落过程中，由于失去了拱的支撑作用，拱顶上方的主应力方向发生偏转，与重力方向的夹角增大。

3.4 宏观仓壁卸料压力分析

为明确拱的形成与塌落对筒仓立壁（下称仓壁）压力分布的影响，绘制贮料状态及结拱起始时刻点A、结拱完成时刻点B及拱塌落时刻点C的仓壁压力分布如图10a。值得一提的是，由于是中心卸料，原则上讲左右测墙压力应该是对称分布，然而由于离散元法在生成颗粒单元时，球体单元排布的随机性，以及其散体颗粒性质，左右测墙的压力分布并非完全对称，而是有微小的差别，以左测墙为参考，这种差别不超过8%。图10a中仓壁侧压力采用的是左右测墙压力的平均值。

参考国家规范《粮食钢板筒仓设计规范》（GB50322-2011）第4.2.3条，定义动态压力修正系数（overpressure coefficient）为卸料中动态仓壁压力与静态仓壁压力之比，图10b给出了动态压力修正系数随深高比的分布图。

图10 仓壁侧压力分布

观察图10，在贮料工况、结拱起始点、结拱完成点及拱塌落时刻，仓壁压力均随着深度的增加非线性增大。结拱起始时刻的仓壁压力较贮料静压力相差不大。在筒仓的浅层（深高比小于0.2），动态压力修正系数小于1，即动态仓壁压力小于静态仓壁压力，分析这部分的工程实际意义不大。下面着重分析工程界关心的深层仓壁压力分布。

为了验证模拟结果，图10a中附上按照国家规范[32]计算的仓壁卸料压力值与本文室内试验结果及Hala中心卸料的模型试验研究成果[33]。在筒仓中下部，也即深高比大于0.45，结拱完成值超过了规范计算值，用规范预测本文的仓壁压力值可能是危险的。结拱完成值要低于Hala的试验值，这可能是由于Hala在试验中采用贮料为玉米，本文采用的为圆球颗粒，圆球颗粒的粒间咬合力很小，这一现象与Kobyłka[34]在做数值模拟与验证时的发现相似。从整体上看Hala的室内模型试验结果、本文的试验结果与模拟值（结拱完成值）有较好的一致性，即二者均存在卸料压力的震荡现象，且卸料压力峰值均出现在筒仓下部深高比0.8～0.85之间。

深高比超过0.2时，结拱完成时的超压系数大于1。深高比0.35处，动态压力修正系数最大为2.70（图10b中的b点）。在深高比0.85处，结拱完成时的仓壁压力最大，达到3.57 kPa。这一结论与本文室内试验结果及Hala[33]的室内模型试验结果接近，此处的超压系数为2.18（图10b中的a点）。即仓壁压力峰值作用点和最大动态压力修正系数作用点并不一致。

3.5 细观动态成拱机制对宏观仓壁卸料压力分布的影响

综合离散元分析结果，结合图6－图10可知，卸料中的成拱机制是动态的，拱效应的存在是卸料中仓壁压力增大以及震荡变化的主要原因。

卸料是颗粒流出卸料口的过程，在拱形成之前，位于仓体上部的颗粒体系遍布弱力链，其颗粒流速较大，宏观表现是此时仓壁卸料压力较小。由于颗粒流动时重新排列组合，其间必然存在相对位移产生摩擦阻力，这些阻力沿着流动方向逐渐增大，在卸料口处达到最大值。此时，筒仓上部阻力小，颗粒流速较快（图6d），而下部流速较慢，上部颗粒的流动会对下部颗粒产生压实作用，从而导致卸料口附近的颗粒物质挤压成拱。成拱的细观表现是料口附近力链强度增大、竖向应力及横向应力的增大，主应力方向的规律化，宏观表现是拱脚处的仓底压力达到局部极大值，作用在仓壁上的卸料压力增大，最大达到静态贮料仓壁压力的2.7倍。

由于拱的形成，阻碍了上部颗粒的运动，细观表现是拱顶周围颗粒流速减小，力链强度增大，竖向应力和横向应力的增大，拱圈内部的颗粒流速则达到最大，遍布弱力链。一方面，拱圈内部颗粒不断的流出，创造着新的临空面。另一方面，拱顶上方的颗粒由于受到拱的阻碍，施加给拱更大的挤压力，当挤压力累加到拱无法承受时，拱开始塌落，此时，拱体的力链强度迅速减小，竖向应力和横向应力减小，主应力方向的无序化，宏观表现则是仓壁卸料压力的减小。

之后，随着物料的流出，仓内贮料不断的重复“结拱起始-结拱完成-拱塌落”的动态成拱过程，因而反映在宏观上则是仓壁卸料压力呈现“较小-局部极大-较小”的震荡分布。

4 结 论

本文采用离散元方法和室内模型试验模拟了筒仓贮料工况及卸料工况，模型试验结果验证了离散元法结果。通过系统的研究结拱起始、结拱完成和拱塌落等时间节点的贮料力链网络、竖向应力和横向应力、颗粒速度及仓壁压力分布，从细观颗粒层次探讨了卸料过程中的动态成拱机制，以及由此引发的宏观仓壁侧压力分布。主要得出以下结论：

1）贮料工况下，同一高度的竖向应力在水平方向上非线性变化，同一横向位置的横向应力在竖直方向上非线性变化。

2）卸料中，仓壁及仓底压力处于周期性变化的状态。

3）卸料中，筒仓底部的卸料口附近有拱形成，其跨度约为卸料口直径的4倍，高度约为卸料口直径的2.5倍。

4）拱的形成导致卸料过程中仓壁压力增大，拱塌落使得仓壁压力减小。动态成拱机制即“结拱（结拱起始-结拱完成）-拱塌落”导致仓壁的卸料压力呈现“较小-局部极大-较小”的震荡分布。

5）工程界关心的仓壁压力峰值作用点在筒仓下部深高比0.85处。

6）本文的动态压力修正系数最大值为2.70，位于深高比0.35处。

[1] 陈长冰，梁醒培. 筒仓卸料过程的离散元模拟分析[J]. 粮油食品科技，2008，16(1)：11－13.

Chen Changbing, Liang Xingpei. Analysis on discrete element simulation of discharging in silos[J]. Science and Technology of Cereals, Oils and Foods, 2008, 16(1): 11－13. (in Chinese with English abstract)

[2] Kobyłka R, Molenda M. DEM simulations of loads on obstruction attached to the wall of a model grain silo and of flow disturbance around the obstruction[J]. Powder Technology, 2014, 256: 210－216.

[3] 刘定华，郭明昌，杨建斌. 筒仓仓壁动态压力的测试和分析[J]. 西安建筑科技大学学报：自然科学版，1989，21(1)：108－113.

Liu Dinghua, Guo Mingchang, Yang Jianbin. Test and analysis on dynamical pressure to the wall of silo[J]. Journal of Xi’an University of Architecture & Technology: Natural Science Edition, 1989, 21(1): 108－113. (in Chinese with English abstract)

[4] 李国柱，刘定华. 筒仓动态压力的计算和测试[J]. 宁波高等专科学校学报，2000，12(4)：1－7.

Li Guozhu, Liu Dinghua. Calculation of dynamic pressure on reinforced concrete silo[J]. Journal of Ningbo College, 2000, 12(4): 1－7. (in Chinese with English abstract)

[5] Wang Peijun, Zhu Xulin, Liu Mei, et al. Buckling behaviors and simplified design method for steel silos under locally distributed axial load[J]. Journal of Constructional Steel Research, 2017, 134: 114－134.

[6] 赵松. 筒仓贮料压力分析及其应用[D]. 武汉：武汉理工大学，2013.

Zhao Song. Analysis and Application for Silo Storage Pressure[D]. Wuhan: Wuhan University of Technology, 2013. (in Chinese with English abstract)

[7] 车颖文. 筒仓的受力情况和稳定性研究[D]. 武汉：武汉理工大学，2011.

Che Yingwen. Research on the Stress Behavior and Stability of the Silos[D]. Wuhan: Wuhan University of Technology, 2013. (in Chinese with English abstract)

[8] 孙其诚，王光谦. 静态堆积颗粒中的力链分布[J]. 物理学报，2008，57(8)：4667－4674.

Sun Qicheng, Wang Guangqian. Force distribution in static granular matter in two dimensions[J]. Acta Physica Sinica, 2008, 57(8): 4667－4674. (in Chinese with English abstract)

[9] 邹同彬，陆渝生，连志颖. 动光弹实验中的主应力分离方法[J]. 解放军理工大学学报：自然科学版，2004，5(4)：72－76.

Zou Tongbin, Lu Yusheng, Lian Zhiying. Separation of principal stress in dynamic photoelastic experiment[J]. Journal of PLA University of Science and Technology, 2004, 5(4): 72－76. (in Chinese with English abstract)

[10] 谭援强，肖湘武，郑军辉，等. 锥形改流体下部孔径对筒仓卸料流态的影响[J]. 农业工程学报，2016，32(19)：82－87.

Tan Yuanqiang, Xiao Xiangwu, Zheng Junhui, et al. Effect of outlet diameter of cone-in-cone insert on silo flow pattern[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(19): 82－87. (in Chinese with English abstract)

[11] 俞良群，邢纪波. 筒仓装卸料时力场及流场的离散单元法模拟[J]. 农业工程学报，2000，16(4)：15－19.

Yu Liangqun, Xing Jibo. Discrete element method simulation of forces and flow fields during filling and discharging materials in silos[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2000, 16(4): 15－19. (in Chinese with English abstract)

[12] 肖昭然，王军，何迎春. 筒仓侧压力的离散元数值模拟[J]. 河南工业大学学报：自然科学版，2006，27(2)：10－12，16.

Xiao Zhaoran, Wang Jun, He Yingchun. The DEM simulation of the lateral pressure of silo[J]. Journal of Henan University of Technology: Natural Science Edition, 2006, 27(2): 10－12, 16. (in Chinese with English abstract)

[13] 张昭，刘克瑾，肖昭然，等. 筒仓仓壁摩擦对仓壁侧压力影响的研究[J]. 河南工业大学学报：自然科学版，2017，38(5)：88－92.

Zhang Zhao, Liu Kejin, Xiao Zhaoran, et al. Influence of the wall friction on the lateral pressure of silo wall[J]. Journal of Henan University of Technology: Natural Science Edition, 2017, 38(5): 88－92. (in Chinese with English abstract)

[14] Oldal I, Keppler I, Csizmadia B, et al. Outflow properties of silos: The effect of arching[J]. Advanced Powder Technology, 2012, 23(3): 290－297.

[15] Goda T J, Ebert F. Three-dimensional discrete element simulations in hoppers and silos[J]. Powder Technology, 2005, 158(1/2/3): 58－68.

[16] Matchett A J. The shape of the cohesive arch in hoppers and silos-Some theoretical considerations[J]. Powder Technology, 2007, 171(3): 133－145.

[17] Cheng Y M, Chau K T, Xiao L J, et al. Flow pattern for a silo with two layers of materials with single or double openings[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(9): 1278－1286.

[18] 唐福元，冯家畅，程绪铎. 大豆籽粒弹性模量的测定与研究[J]. 粮食储藏，2015，44(5)：6－9.

Tan Fuyuan, Feng Jiachang, Cheng Xuduo. Determination and study on the elastic modulus of soybean seeds[J]. Grain Storage, 2015, 44(5): 6－9. (in Chinese with English abstract)

[19] 冯家畅，程绪铎，严晓婕. 大豆与仓壁材料摩擦系数的研究[J]. 大豆科学，2014，33(5)：787－789+794.

Feng Jiachang, Cheng Xuduo, Yan Xiaojie. Research on the coefficient of friction between soybean and silo wall material[J]. Soybean Science, 2014, 33(5): 787－789+794. (in Chinese with English abstract)

[20] 程绪铎，陆琳琳，石翠霞，等. 大豆内摩擦角的测定与实验研究[J]. 粮食储藏，2010，39(5)：12－15.

Cheng Xuduo, Lu Linlin, Shi Cuixia, et al. Measurement and experimenta on internal friction angle of soybean[J]. Grain Storage, 2010, 39(5): 12－15. (in Chinese with English abstract)

[21] 冯家畅，程绪铎，杜小翠，等. 大豆堆压缩密度与体变模量研究[J]. 中国粮油学报，2016，31(12)：112－117.

Feng Jiachang, Cheng Xuduo, Du Xiaocui, et al. Compressive density and bulk modulus of soybean[J]. Journal of the Chinese Cereaks and Oils Association, 2016, 31(12): 112－117. (in Chinese with English abstract)

[22] Janssen H A. Experiments about pressure of grain in silos[J]. VDI, 1895: 1045－1049.

[23] 孙其诚，辛海丽，刘建国，等. 颗粒体系中的骨架及力链网络[J]. 岩土力学，2009，30(增刊1)：83－87.

Sun Qicheng, Xin Haili, Liu Jianguo, et al. Skeleton and force chain network in static granular material[J]. Rock and Soil Mechanics, 2009, 30(Supp.1): 83－87. (in Chinese with English abstract)

[24] 房营光，侯明勋，谷任国，等. 桩承式路堤中土拱效应产生过程可视化分析[J]. 岩土工程学报，2015，37(9)：1678－1684.

Fang Yingguang, Hou Mingxun, Gu Renguo, et al. Visual analysis of initiation of soil arching effect in piled embankments[J]. Rock and Soil Mechanics, 2015, 37(9): 1678－1684. (in Chinese with English abstract)

[25] 程奇鹏，孙巍巍，卢赛. 基于PFC3D的浅圆仓偏心卸料离散元研究[J]. 土木工程与管理学报，2016，33(6)：43－47.

Cheng Qipeng, Sun Weiwei, Lu Sai. Discrete element analysis of squat silo under eccentric discharge by PFC3D[J]. Journal of Civil Engineering and Management, 2016, 33(6): 43－47. (in Chinese with English abstract)

[26] 张大英，许启铿，王树明，等. 筒仓动态卸料过程侧压力模拟与验证[J]. 农业工程学报，2017，33(5)：272－278，316.

Zhang Daying, Xu Qikeng, Wang Shuming, et al. Simulation and experimental validation of silo wall pressure during discharging[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(5): 272－278, 316. (in Chinese with English abstract)

[27] Cannavaccuiolo A, Barletta D, Dosi G, et al. Arch-Free flow in aerated silo discharge of cohesive powders[J]. Powder Technology, 2009, 191(3): 272－279.

[28] 韩高孝，宫全美，周顺华. 摩擦型岩土材料土拱效应微观机制颗粒流模拟分析[J]. 岩土力学，2013，34(6)：1791－1798.

Han Gaoxiao, Gong Quanmei, Zhou shunhua. Analysis of microcosmic mechanism of soil arching in frictional geotechnical material by particle flow simulating[J]. Rock and Soil Mechanics, 2013, 34(6): 1791－1798. (in Chinese with English abstract)

[29] Christoffersen J, Mehrabadi M M, Nemat-Nasser S. A micromechanical description of granular material behavior[J]. J Appl Mech, 1981, 48: 339－344.

[30] Fortin J, Millet O, de Saxcé G. Construction of an averaged stress tensor for granular medium[J]. European Journal of Mechanics A/Solids, 2003, 22: 567－582.

[31] 赖汉江，郑俊杰，章荣军，等．桩承式路堤土拱形成及荷载传递机制离散元分析[J]．岩土力学，2015，36(增刊1)：646－650.

Lai Hanjiang, Zheng Junjie, Zhang Rongjun, et al. Discrete element analysis of development and load-transfer mechanism of soil arching within piled embankment[J]. Rock and Soil Mechanics, 2015, 36(Supp.1): 646－650. (in Chinese with English abstract)

[32] 粮食钢板筒仓设计规范GB50322-2011[S]. 北京：中国计划出版社，2001.

[33] Hala Hammadeh. Flow and Pressure during Centric and Eccentric Discharge in Cylindrical Silos[J]. Science & Technology, 2012: 44－48.

[34] Kobyłka R, Molenda M. DEM modelling of silo load asymmetry due to eccentric filling and discharge[J]. Powder Technology, 2013, 233: 65－71.

Development of arching and silo wall pressure distribution in storage and discharging state based on discrete element analysis

Liu Kejin, Xiao Zhaoran, Wang Shihao

(450001)

It has been widely recognized that the most dangerous condition is the phenomenon that the emptying pressure on the wall of silos vibrates and increases obviously during discharging. However, the cause of this phenomenon is currently largely unknown. Most of the available papers and reports are based on continuum mechanics, that is, the stored material is regarded as a continuous entity on macroscopic level, and its particulate property is ignored. In fact, it is the microcosmic mechanical behavior of individual particles and the interaction between the particles and the silo walls that determine the emptying pressure distribution on the silo walls. Therefore, in this paper, the characteristics of emptying pressure were studied from the point of view of granular materials and microcosmic particle mechanics. A new method combining particle mechanics with discrete element method (DEM) was introduced to explore how the mechanical behavior of particles effects the distribution of emptying pressure. Firstly, the behavior of granular material in stored state was studied by DEM method. The silo with flat bottom is 0.5 m in diameter, 1.0 m in height and 0.1 m in outlet diameter, which is filled with 20 400 spherical particles. The distribution of the static wall pressure in stored state was verified by the test results and the Jassen Formula which is widely used in engineering. Secondly, the pressure distribution on the silo bottom wall was studied by simulating the discharge process, and the statistical analysis of multiply simulation results was performed, the arching effect near the outlet were proved according to the periodic pressure profile. Thirdly, in order to study the arching effect, three time points, i.e. start of arching, completion of arching and arch collapse, were selected on the periodic pressure profile. For each time point, the behaviors, such as force chain network, vertical stress distribution, and lateral stress distribution, the direction of principal stress, velocity field of granular material and so on, were systematically studied. On this basis, the features and evolution mechanism of the arching effect were investigated from the viewpoint of particle mechanics. Finally, the static pressure under the static stored state and the emptying pressure in discharging process on the silo wall were analyzed and verified by a model test, Standards (GB50322-2011) and published results. The results indicated that the arch which is 4.0 times wide of outlet diameter and 2.5 times high of outlet diameter was produced during the discharge process. Due to the formation of arching, the vertical stress above arching was transformed into the horizontal stress in a certain range above the arch foot, thus the horizontal stress was transferred to both sides of the silo wall and to the pressure of the silo wall was increased. When the arching collapsed, the vertical and horizontal above arching decreased, then the horizontal stress transferred to both sides of the silo wall also decreased, which resulted in to the decrease of wall pressure. The coefficient of overpressure reached a peak value of 2.70 at depth ratio of 0.35, while the peak wall pressure was 3.57 kPa at depth ratio of 0.85. It was found that the arching effect near the outlet behaved dynamically, following the rule of “start of arching-completion of arching-collapse of arch”, thus the dynamic arching effect is put forward. In addition, the important connection between the dynamic arching effect and the resulting emptying pressure distribution was identified. That is, the increased emptying pressure on silo wall is caused by the formation of arch, while the vibration of emptying pressure on wall of silo is induced by the dynamic arching effect. The research provides a new method of exploring the relationship between the arching effect and the emptying pressure distribution on wall of silos from the micro and macro aspects. The findings obtained in this paper can provide references for revealing the load-transfer mechanism from particles to silo wall.

stresses; numerical methods; silos; wall pressure; arch; soybean; granular materials; micromechanics

10.11975/j.issn.1002-6819.2018.20.035

S126

A

1002-6819(2018)-20-0277-09

2017-12-08

2018-07-19

国家自然科学基金项目（5170081095）；河南工业大学高层次人才基金（31400375）

刘克瑾，讲师，博士。主要从事粮食颗粒的力学性质、筒仓结构设计和地基处理研究。Email：Kejin_Liu@126.com

刘克瑾,肖昭然,王世豪. 基于离散元模拟筒仓贮料卸料成拱过程及筒仓壁压力分布[J]. 农业工程学报，2018，34(20)：277－285. doi：10.11975/j.issn.1002-6819.2018.20.035 http://www.tcsae.org

Liu Kejin, Xiao Zhaoran, Wang Shihao. Development of arching and silo wall pressure distribution in storage and discharging state based on discrete element analysis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(20): 277－285. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.20.035 http://www.tcsae.org