玻璃温室和塑料大棚内逐时气温模拟模型

韦婷婷，杨再强,2**，王 琳，赵和丽，李佳帅



玻璃温室和塑料大棚内逐时气温模拟模型

韦婷婷1，杨再强1,2**，王 琳1，赵和丽1，李佳帅1

（1．南京信息工程大学气象灾害预报预警与评估协同创新中心，南京 210044；2．江苏省农业气象重点实验室，南京 210044）

2014−2016年在江苏省不同地区选择塑料大棚和玻璃温室进行设施内气温监测，基于设施内日最高和最低气温，采用余弦分段函数、正弦分段函数、正弦−指数分段函数、一次分段函数和神经网络模型分别模拟不同季节和不同天气状况（晴天和阴雨天）下的逐时气温日变化，探究利用室内最高和最低气温模拟计算逐时气温的方法，以及设施内逐时气温日变化规律。结果表明：5种模型均可通过当日最高、最低气温模拟逐时气温变化，其中神经网络模拟精度较高（RMSE=0.69℃），并且受温室类型、天气状况和季节变化的影响较小，普适性较高；正弦−指数分段函数模拟效果最好（RMSE=0.43℃），且受天气和季节的影响较小，但其受温室本身特性和地区的影响较大；余弦分段函数（RMSE=0.85℃）和正弦分段函数（RMSE=0.78℃）模拟效果相近，且受天气和地区的影响；一次分段函数准确度较低（RMSE=0.90℃）且误差变化较大。各方法对塑料大棚内逐时气温的模拟精度均高于玻璃温室。模型模拟精度的季节变化因模型和温室类型有一定差异，但通常情况下，春季和冬季的模拟误差大于秋季，夏季误差最小。

塑料大棚；玻璃温室；温度模拟；温室；气温日变化

在中国南方地区，塑料大棚和玻璃温室已经在蔬菜和水果种植中得到广泛应用。温室内气温的变化不仅关系到室内作物的生长发育以及产量形成，对果实的品质也有重要影响。故研究温室内气温的变化对调节温室环境，防御相关气象灾害有一定帮助，同时也可以为人工气候箱试验的动态气温设置[1−2]提供理论依据。

近年来，不少学者通过物理模型和统计模型对温室气温的日变化进行了模拟。物理方法主要包括能量平衡方法[3−4]和流体动力学方法[5−6]，这些方法具有很强的机理性，可释度高，但是需要大量的相关参数作支持，通常情况下，所需参数的值难以准确计算，导致模拟过程复杂，结果出现误差。同时，也有大量学者尝试利用统计模型通过室外气象要素对温室气温进行预测，主要集中在对温室最高、最低气温的预测[7−12]。杨文刚等[13]研究了春季不同类型温室气温的回归预测方程。刘淑梅等[14−15]运用BP神经网络的方法分别建立了对日光温室和塑料大棚内气温的预测模型。李倩等[16−17]对南方地区单栋塑料大棚和双膜塑料大棚内气温进行了谐波模拟，得到了较好的结果。但在模拟计算室内逐时气温时，通常要求有长期的室外逐时气象数据作为支持，这对大部分温室而言是一个难点。

对于室外气温，Reicosky等[18]提出并总结了用最高、最低气温模拟室外逐时气温的方法，并得到广泛应用。余卫东等[19]运用正弦−指数分段函数对室外气温的日变化进行了模拟。姜会飞等[20]应用正弦分段法对气温的日变化进行了模拟。徐凡等[21]也使用了数学方法对温室外的气温日变化进行了模拟，得到华北地区室外气温的转化系数。有研究表明温室内气温变化与室外气温变化总体上一致[22]，但是在冬季可能会出现延迟。所以适用于模拟室外逐时气温的方法对温室内气温可能也同样适用，但是目前并没有相关研究证明这一点。

本研究使用余弦分段函数（WAVE）、正弦分段函数（WCALC）、正弦−指数分段函数（TEMP）、一次分段函数（SAWTOOTH）以及近年来常用的BP神经网络预测模型模拟了江苏地区常见温室类型（塑料大棚和玻璃温室）在不同季节、不同天气条件下的气温逐时变化，并对模型的精度进行比较，拟在证明在不同天气和温室类型下利用设施内日最高、最低气温模拟气温动态变化的可行性，并且分析不同模型在不同条件下的模拟特点，以选取普适性较高的模型。

1 材料与方法

1.1 研究区域和资料获取

选取江苏省句容、泰州、南京3个地区的2栋塑料大棚和2栋玻璃温室（表1），于2014−2016年在各温室内距地面1.5m处架设CR-3000数据采集器（美国），观测要素包括气温、相对湿度、日照时数、太阳总辐射，数据采集频率为每10s一次，存储每小时的平均值。以3月1日−5月31日为春季，6月1日−8月31日为夏季，9月1日−11月30日为秋季，12月1日−翌年2月28日为冬季，在每个季节根据日照百分率以及室外降水情况选取一个典型晴天和典型阴雨天进行模拟，其中典型晴天日照百分率超过90%且无降水，阴雨天气日照百分率低于10%或有降水。

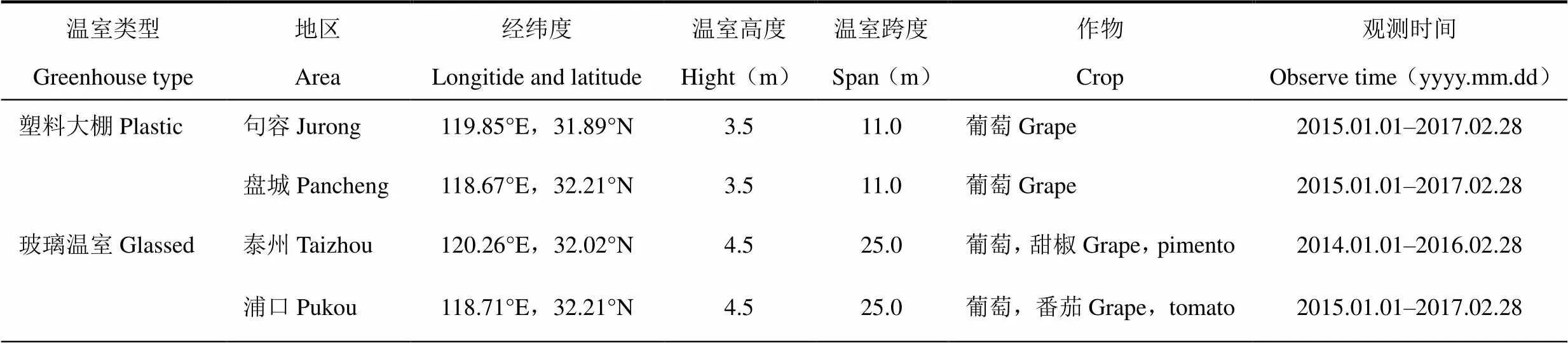
表1 研究地点概况

1.2 模拟方法及相关参数的计算

1.2.1 余弦分段函数（WAVE）

该方法认为气温的日变化是关于最高、最低气温和时间的余弦函数，且认为当日最低气温出现在日出前后，最高气温出现在午后，只需输入当日最高、最低气温，即可模拟其逐时变化过程[18，23]。

1.2.2正弦分段函数（WCALC）

该方法需要连续3d的最高、最低气温作为输入值，可以模拟出中间一天的逐时气温，它将一天分为3段，认为午夜至日出后2h气温逐渐呈线性降低，日出后2h至日落时刻气温的变化可以用一个正弦函数表示，日落后至午夜气温呈线性降低[24−25]。日出时间和日落时间由测点经纬度计算得到，为便于计算逐时气温，认为江苏地区春夏季节日出时间为6：00，日落时间为19：00；秋冬季节日出时间为7：00，日落时间为18：00。

1.2.3 正弦−指数分段函数（TEMP）

此方法认为日出时−日落时，气温按正弦曲线变化，日落后气温按指数曲线减小[18,20,25]。日落时间和日出时间的确定方法与正弦分段函数法相同。

1.2.4 一次分段函数（SAWTOOTH）

该方法认为气温的日变化是直线递增（递减）的，呈锯齿状波动，用3个一次函数即可模拟[18]。对观测样本进行统计后，认为春秋季节最低温出现在6：00，最高温出现在15：00，夏季最低温出现的时间提前1h，冬季则延后1h，最高温出现时间不变。

1.2.5 神经网络法（BP）

将观测期间第一年的室内气温数据作为建模数据，每个季节随机选取77d逐时气温数据作为训练样本，经过归一化处理后，隐含层中设置最高、最低气温和时刻3个节点，隐含层和输出层传递函数采用S型对数函数Logsig[26]，之后用剩余15d的逐时气温数据作为检验样本，以提高模型精度。神经网络的相关参数分别设置为：初始学习速率η为0.1，惯量因子α为0.9，最大迭代次数为1000次，目标误差为0.00004。神经网络模型采用 Matlab2016a软件通过编程实现。在模型使用过程中，只需要输入当天的最高、最低气温就可以模拟任意时刻的室内气温。

1.3 模拟结果检验参数

相关系数（皮尔逊相关系数R）是衡量两组数据之间线性相关程度的量，R越趋近于1，则表示模拟结果与实测值相关性越好，结果越精确。均方根误差（Root Mean Square Error，RMSE）可以反应误差的离散程度，RMSE越小表示模拟效果越好。平均偏差（Mean Bias Error，MBE）主要考虑了误差的正负，可以反映模型高估或低估了实际情况，MBE越接近0，模拟效果越好。相应计算式为

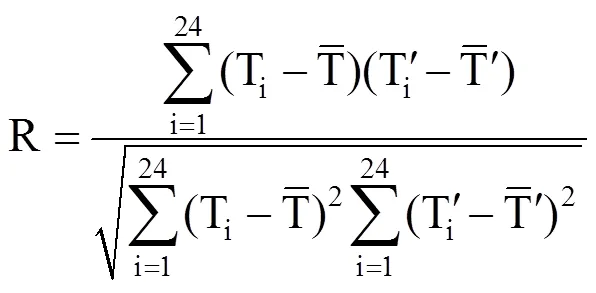
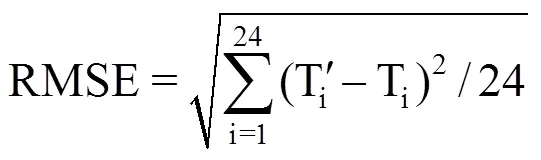
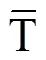
2 结果与分析

2.1 塑料大棚室内逐时气温变化过程模拟结果比较

2.1.1 各季节模拟结果的比较

在句容和盘城地区，基于2016年逐日观测数据，分别利用5种模型模拟塑料大棚温室内逐时气温的变化过程，每日同一时刻室内气温平均后得到各季节逐时气温的变化过程，与相应实测数据的平均值进行对比，结果见图1。由图可见，5种模型模拟的逐时气温变化过程与实测数据分布特点基本一致，均表现为0：00−9：00逐渐降低，9：00−15：00快速升高，15：00−24：00逐渐降低的过程，只是各模型曲线与实测曲线的拟合程度略有不同。表2为5种模型对塑料大棚内四季逐时平均气温模拟精度。为便于比较模型总体误差，计算句容地区5种模型全年的平均模拟误差（忽略季节影响，取四季平均值，后同）分别为0.86、0.78、0.31、0.92和0.76℃（分别对应余弦分段函数WAVE、正弦分段函数WCALC、正弦−指数分段函数TEMP、一次分段函数SAWTOOH和神经网络模型BP，下同），其中TEMP模拟效果最好，夏季误差最小，且其平均偏差（MBE）为负值，表明预测结果略高于实际气温；BP的模拟效果在整体上仅次于TEMP模型，但其在不同季节模拟效果差异较大，在夏季模拟效果最差，秋季模拟效果较好，预测结果也稍高于实际气温；WCALC的模拟精度较高，其随季节变化并不明显，其MBE较低，且通常为正值，即模拟结果稍低于实际气温；WAVE的模拟效果一般，在春夏季稍好，MBE也为负值，且在夏季绝对值最小；SAWTOOH的模拟效果较差，特别是在春季和冬季。对于盘城地区，5种模型全年的平均误差分别为0.24、0.41、0.34、0.22和0.40℃，与句容地区相比，盘城塑料大棚的模拟结果更好一些，并且不同模型的精度提高程度也不同，但各模型模拟结果的MBE的特点并未改变。SAWTOOH对盘城地区的模拟效果最好，与句容地区相比误差减小了76.1%，模型在4个季节均有良好的模拟精度，特别是在夏季；WAVE的模拟精度也有较大提高，误差减少了72.1%，在春夏季节的模拟情况好于秋冬季节；TEMP模型的模拟情况与句容地区相似，误差较小且在夏季误差最小；BP模型的误差也减少了47.3%，同样在秋季的模拟效果最好；WCALC函数的模拟误差与BP模型相近，与句容地区相比，误差减少了47.4%，且在冬春季节的误差较大。

综上，5种模型均可根据日最高、最低气温模拟塑料大棚内气温的逐时日变化，5种模型的平均误差分别为0.55、0.59、0.32、0.57、0.58℃。对于不同的塑料大棚，TEMP模型都有较良好的拟合效果，预测结果稍高于实际气温；SAWTOOH和WAVE对不同塑料大棚的模拟效果差异较大，预测结果高于实际气温；WCALC和BP对不同塑料大棚的模拟效果有一定差异，并且WCALC的模拟结果略低于实际气温，BP则高估实际气温。从季节变化而言，5种模型的拟合效果在冬季都要稍差一些，TEMP在夏季模拟效果最好，BP在秋季模拟效果最好，WAVE在春夏季节模拟效果较好，WCALC和SAWTOOH则无季节差异。

2.1.2 各季节典型日模拟结果的比较

在句容和盘城地区，每各季节选取一个典型晴天和典型阴雨天，分别利用5种模型模拟每日塑料大棚温室内逐时气温的变化过程，与相应实测数据进行对比，结果见图2、图3。由图中可见，典型晴天和阴雨天的气温变化趋势相似，只是由于晴天和阴雨天云量的不同，阴雨天云量多，大气保温效果好，故晴天和阴雨天气温变化幅度也不一样，阴雨天的气温通常低于晴天，但全天气温较稳定，波动不明显。晴天条件下，句容地区5种模型的平均模拟误差（忽略季节影响，取四季平均RMSE）分别为1.56、1.55、0.99、1.48和0.95℃，盘城地区分别为0.42、0.67、0.45、0.64和0.62℃，从均方根误差（RMSE）来看，典型晴天下不同塑料大棚的模拟情况与各季节的总体情况相似，从个体的角度再次证明了之前的结论。典型阴雨天条件下，句容地区5种模型的平均均方根误差分别为0.80、0.79、0.66、0.86和0.89℃，盘城地区分别为0.21、0.28、0.26、0.19和0.28℃。可以看出，典型阴雨天的模拟精度与典型晴天相比有明显的提高，但其相关系数（R）较低，晴天条件下，5种模型模拟结果与实测值之间平均相关系数=0.95且R＞0.88，即模型可以较好地描述气温上升和下降时的变化趋势，而阴雨天条件下模拟结果与实测值之间=0.85且R＞0.53，表明模型虽然可以较准确地模拟逐时气温，但是对气温的变化情况描述不够细致。对比不同模型在典型晴天和典型阴雨天下的模拟情况可知，正弦−指数分段函数（TEMP）在晴天和阴雨天气中都有较好的模拟结果，在春夏季节和阴雨天条件下误差较小；神经网络模型（BP）的模拟效果在晴天时仅次于TEMP，但在阴雨天时的模拟误差则无显著减小，受天气情况的影响较小；余弦分段函数（WAVE）、正弦分段函数（WCALC）和一次分段函数（SAWTOOH）在阴雨天的模拟效果明显好于晴天时，说明其受天气和塑料大棚本身的影响较大。

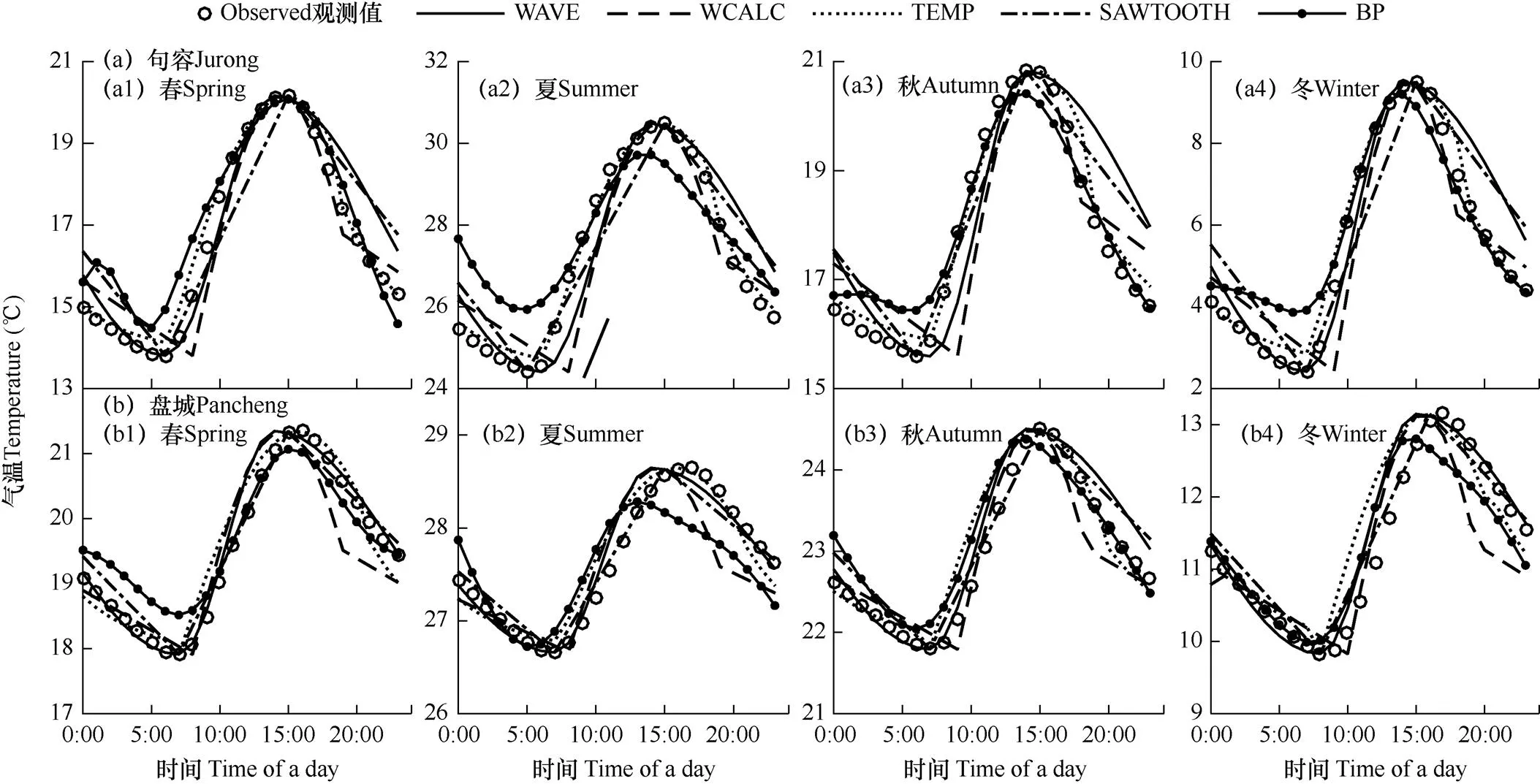
图1 塑料大棚内四季逐时平均气温模拟值与实测值的日内变化

图2 四季典型晴天塑料大棚内逐时气温模拟值与实测值的日内变化

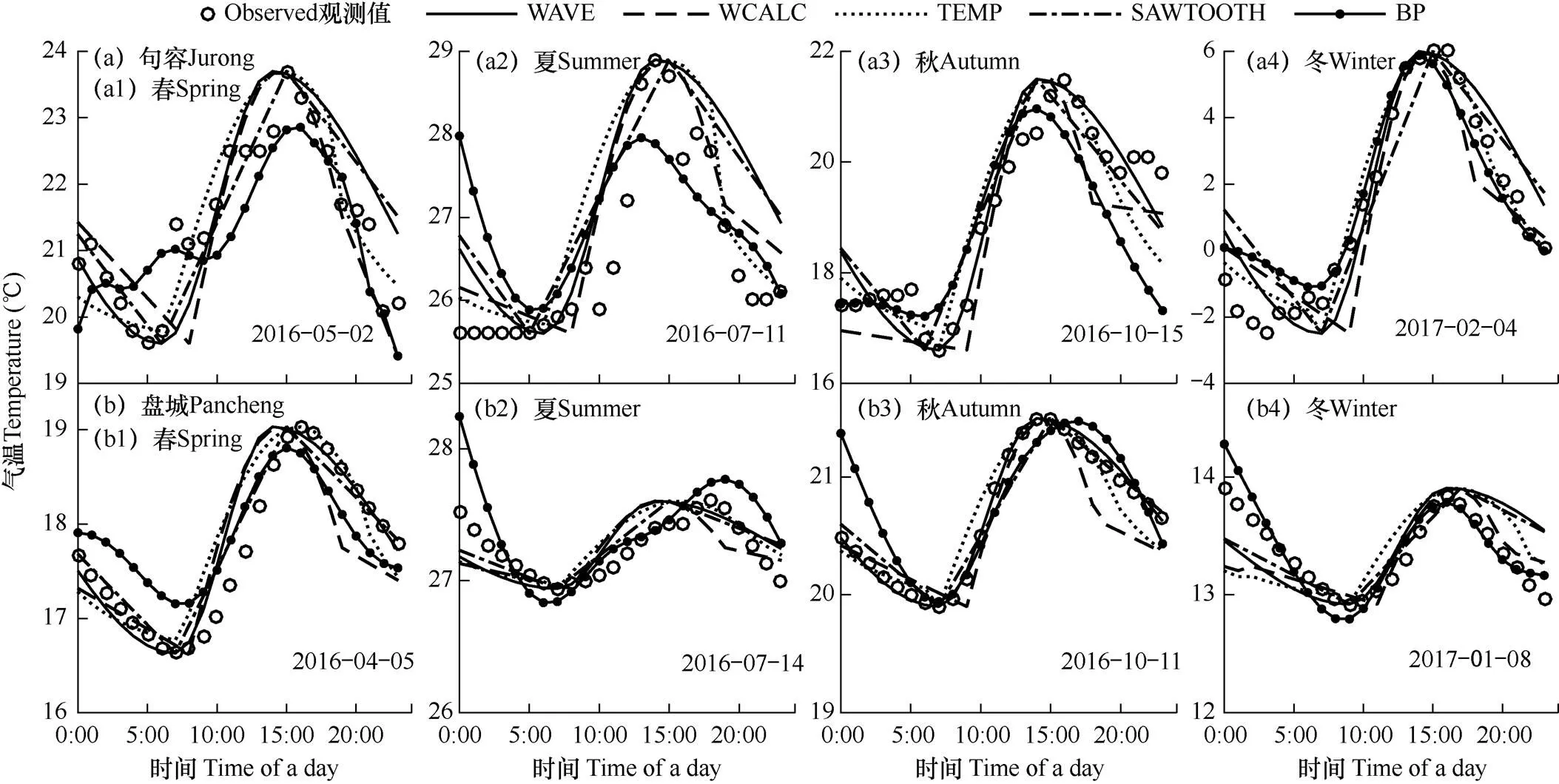
图3 四季典型阴雨天塑料大棚内逐时气温模拟值与实测值的日内变化

表3 四季典型天气条件五种模型对塑料大棚内逐时气温模拟精度

2.2 玻璃温室内逐时气温变化过程模拟结果比较

2.2.1 各季节模拟结果的比较

泰州和浦口地区玻璃温室各季模拟结果比较见图4。由图可见，玻璃温室内的气温变化与塑料大棚内变化趋势一致，5种模型模拟的逐时气温变化过程与实测数据分布特点基本一致。表4为5种模型对玻璃温室内四季逐时平均气温模拟精度的比较。对于泰州地区，5种模型全年平均模拟误差分别为1.24、1.06、0.37、1.29和0.81℃，其中正弦−指数分段函数（TEMP）和神经网络模型（BP）的模拟结果明显好于其它模型，并且都在春夏季节模拟较准确，但从平均偏差（MBE）来看，TEMP的模拟结果高于实测值，而BP的MBE则无明显规律；其次，正弦分段函数（WCALC）的模拟效果仅次于TEMP和BP，其模拟精度随季节的变化差异不明显，预测结果低于实测值；余弦分段函数（WAVE）在春夏季节较精确，预测结果高于实际气温；一次分段函数（SAWTOOH）的模拟结果较差且高于实际气温。浦口地区全年平均误差分别为1.05、0.88、0.72、1.15和0.78℃，对比可知，TEMP的均方根误差与泰州地区相比增加了95%，但其模拟效果依旧好于其它模型，但此时其在秋冬季节的模拟精度较高；BP模型的模拟结果地区间差异并不明显，但其也表现为在秋冬季节的模拟效果较好；WCALC模型的模拟误差相比泰州地区减少了17%，并且在秋季误差较小；WAVE和SAWTOOH的模拟误差相近，均稍高于实际气温并且在夏季误差最小。

综上可知，5种模型均可根据日最高、最低气温模拟玻璃温室内气温的逐时日变化，5种模型的平均误差分别为1.14、0.97、0.55、1.22、0.79℃。对比可知，TEMP模型和BP在模拟精度上具有明显优势，且其季节变化特征在不同的玻璃温室也表现不一；WCALC的模拟效果较好，与其它模型不同的是其模拟结果通常稍低于实测值；WAVE和SAWTOOH的模拟精度较低，且都在夏季模拟效果最好。

2.2.2 各季节典型日模拟结果比较

在泰州和浦口地区，每个季节选取一个典型晴天和典型阴雨天，分别利用5种模型计算每日玻璃温室内逐时气温，与相应实测数据进行对比，结果如图5、图6所示。由图可见，玻璃温室内的气温分布也符合下降—快速上升—快速下降的基本规律，并且晴天和阴雨天的气温分布也与塑料大棚类似，5种模型模拟的逐时气温变化过程与实测数据分布特点基本一致。表5为5种模型对玻璃温室内四季典型晴天和阴雨天逐时平均气温模拟精度的比较。由表可知，晴天条件下，5种模型的平均模拟误差（忽略季节影响，取四季平均RMSE）分别为0.99、1.07、0.76、0.75和0.79℃（泰州），1.69、1.40、1.18、1.94和0.92℃（浦口）。对于泰州玻璃温室的模拟结果，一次分段函数（SAWTOOH）、正弦−指数分段函数（TEMP）以及神经网络模型（BP）的模拟效果较好，并且都在夏秋季节有较小的误差；而对于浦口的玻璃温室则以BP的模拟效果最好，其次为TEMP模型，这与之前对总体情况的分析结果类似。阴雨天气下，5种模型的平均模拟误差分别为1.25、1.23、0.65、1.17、0.77℃（泰州），1.39、1.08、1.07、1.41、0.89℃（浦口），可以看出TEMP和BP的误差较小。对比典型晴天和阴雨天气下的模拟结果可以发现，玻璃温室在典型阴雨天下的模拟精度与典型晴天条件下相比并无明显差异，5种模型在晴天条件下的平均相关系数=0.93（R＞0.85）比其在阴雨天气下的=0.89（R＞0.56）略高，这与塑料大棚的模拟结果略有不同。对比不同模型的模拟情况可知，TEMP和BP的模拟效果在晴天和阴雨天均普遍表现较好，但TEMP的模拟精度随地区的变化差异较大，BP的模拟情况随地区变化不大；WAVE的模拟精度较低且在冬季模拟情况较好。

图4 玻璃温室内四季逐时平均气温模拟值与实测值的日内变化

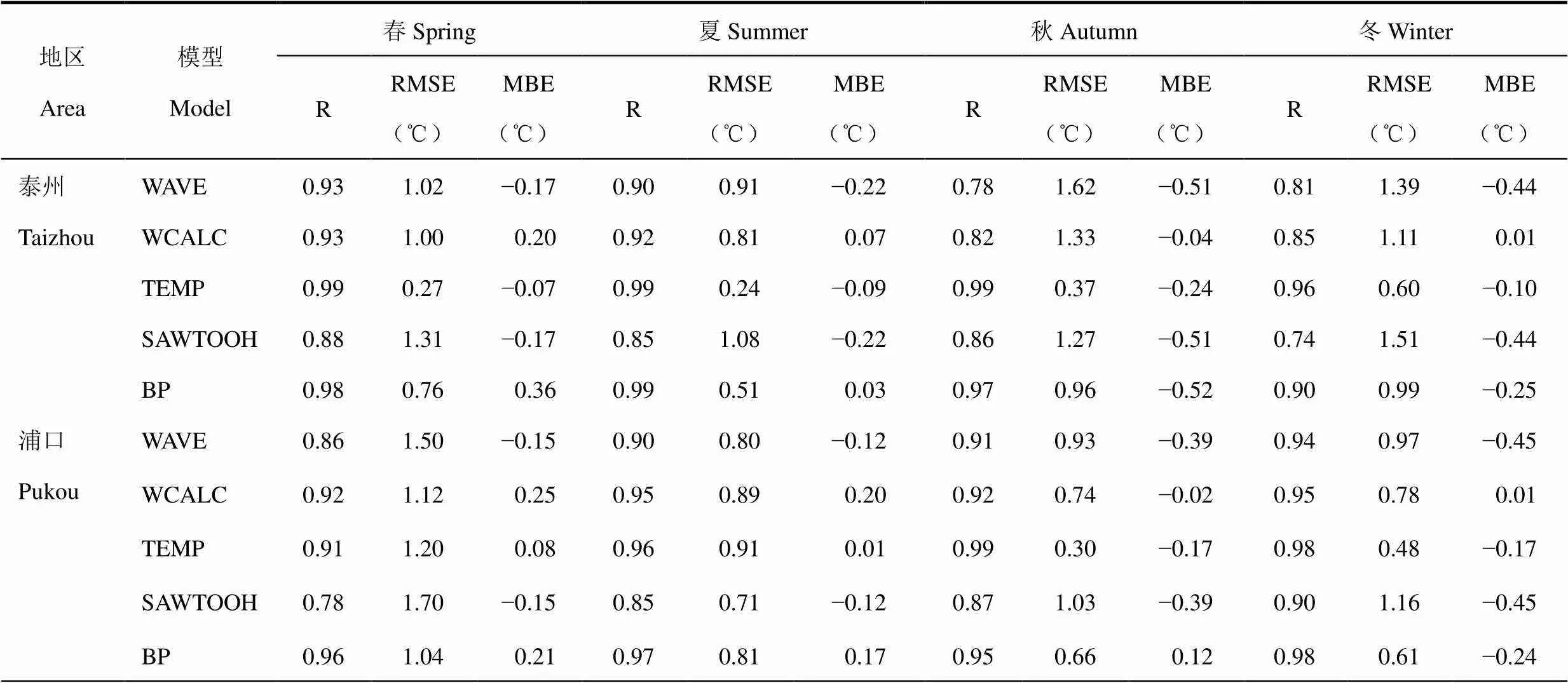
表4 五种模型对玻璃温室内四季逐时平均气温模拟精度

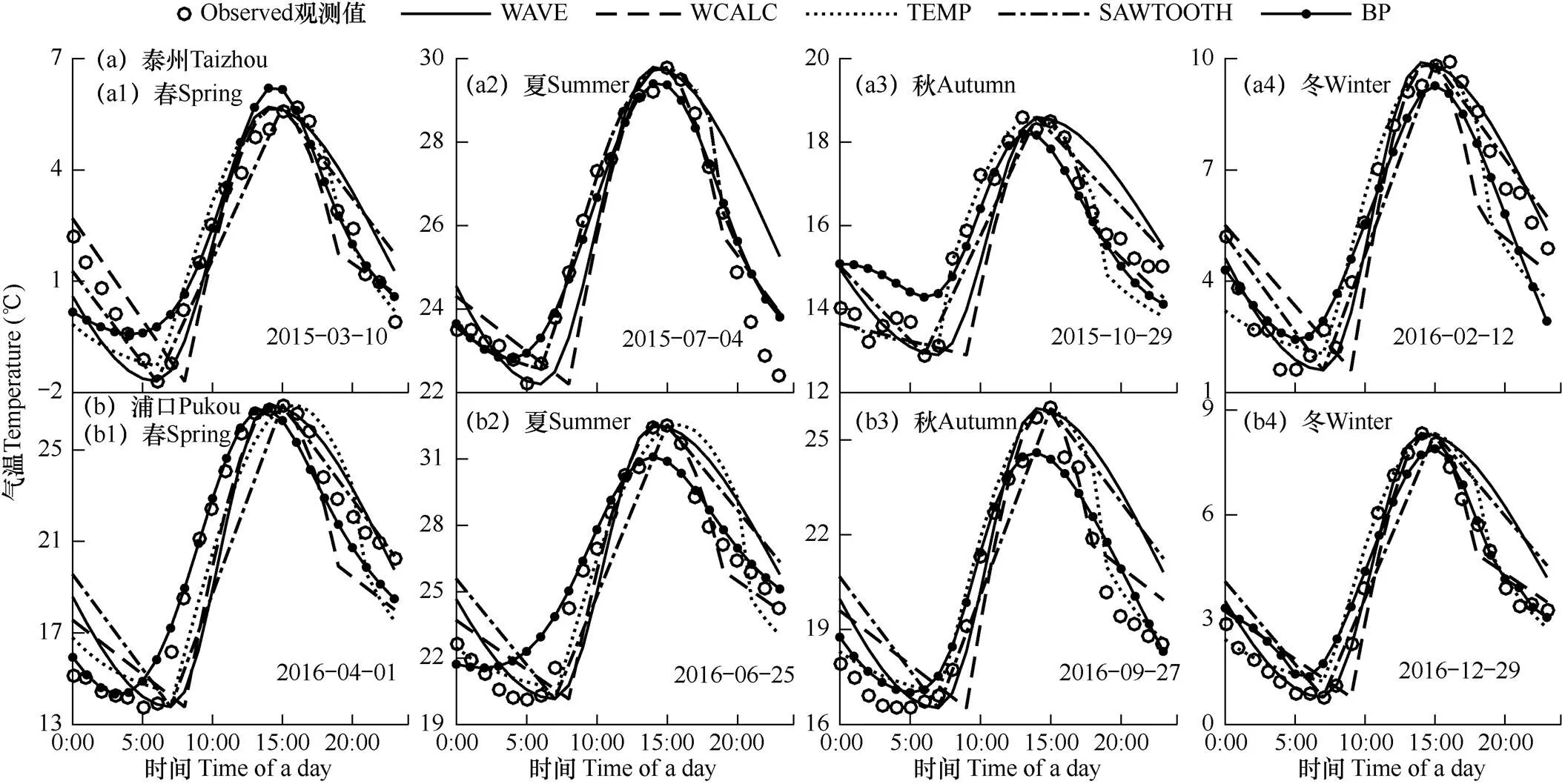
图5 四季典型晴天玻璃温室内逐时气温模拟值与实测值的日内变化

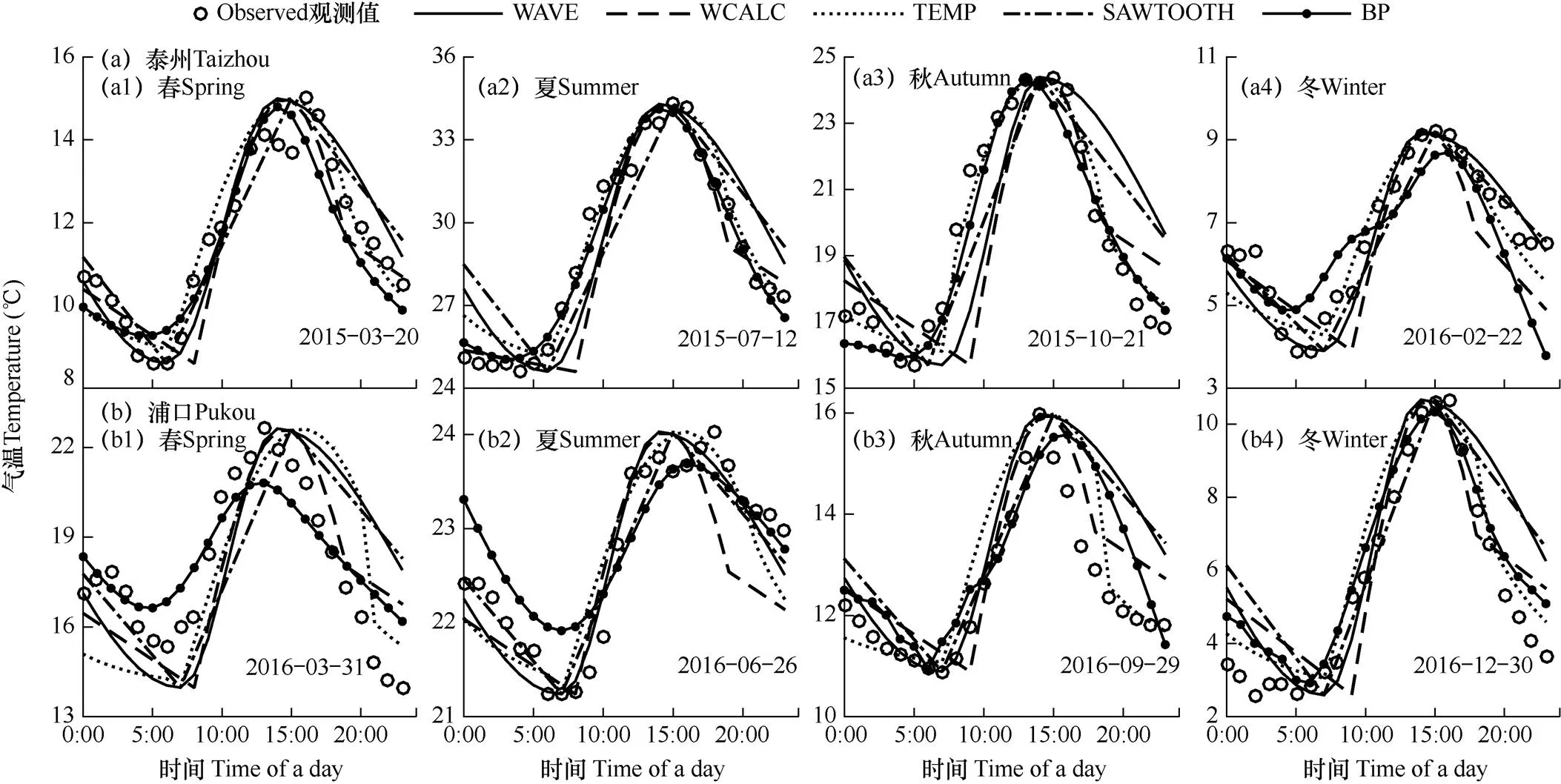
图6 四季典型阴雨天玻璃温室内逐时气温模拟值与实测值的日内变化

2.3 塑料大棚与玻璃温室模拟结果的比较

与塑料大棚的模拟结果相比，玻璃温室的模拟误差较大，5种模型的平均均方根误差分别增加107.7%、64.1%、69.4%、115.6%和36.3%，其中神经网络模型（BP）的误差变化最小，说明其随温室类型的变化模拟差异不明显，余弦分段函数（WAVE）和一次分段函数（SAWTOOH）误差变化较大，说明其普适性较差，正弦−指数分段函数（TEMP）的误差虽然变化较大，但始终维持在一个较低的水平。综合模拟结果可知，天气状况对5种模型的模拟精度也有一定的影响，且对塑料大棚的影响大于对玻璃温室。5种模型在晴天下都能更好地模拟气温的变化过程，但阴雨条件下的误差较小，就对气温的模拟误差而言阴雨条件下模拟情况较为理想。就典型天气下5种模型各自的精度变化来看，TEMP模型的平均误差最小且其变化也较小；BP模型的精度变化最小，其模拟精度仅次于TEMP，故这两种模型的普适性较高；WAVE、WCALC和SAWTOOTH对塑料大棚进行模拟时模拟精度受天气的影响较大，对玻璃温室模拟时其精度较为稳定。5种模型对塑料大棚的模拟精度存在一定的季节变化特征，均表现为在冬季误差较大，TEMP在夏季模拟效果最好，BP在秋季模拟效果最好，WAVE在春夏季节模拟效果较好。而5种模型对玻璃温室的模拟精度则无没有明显的季节变化特征，但TEMP、WAVE均在夏季模拟较为准确。

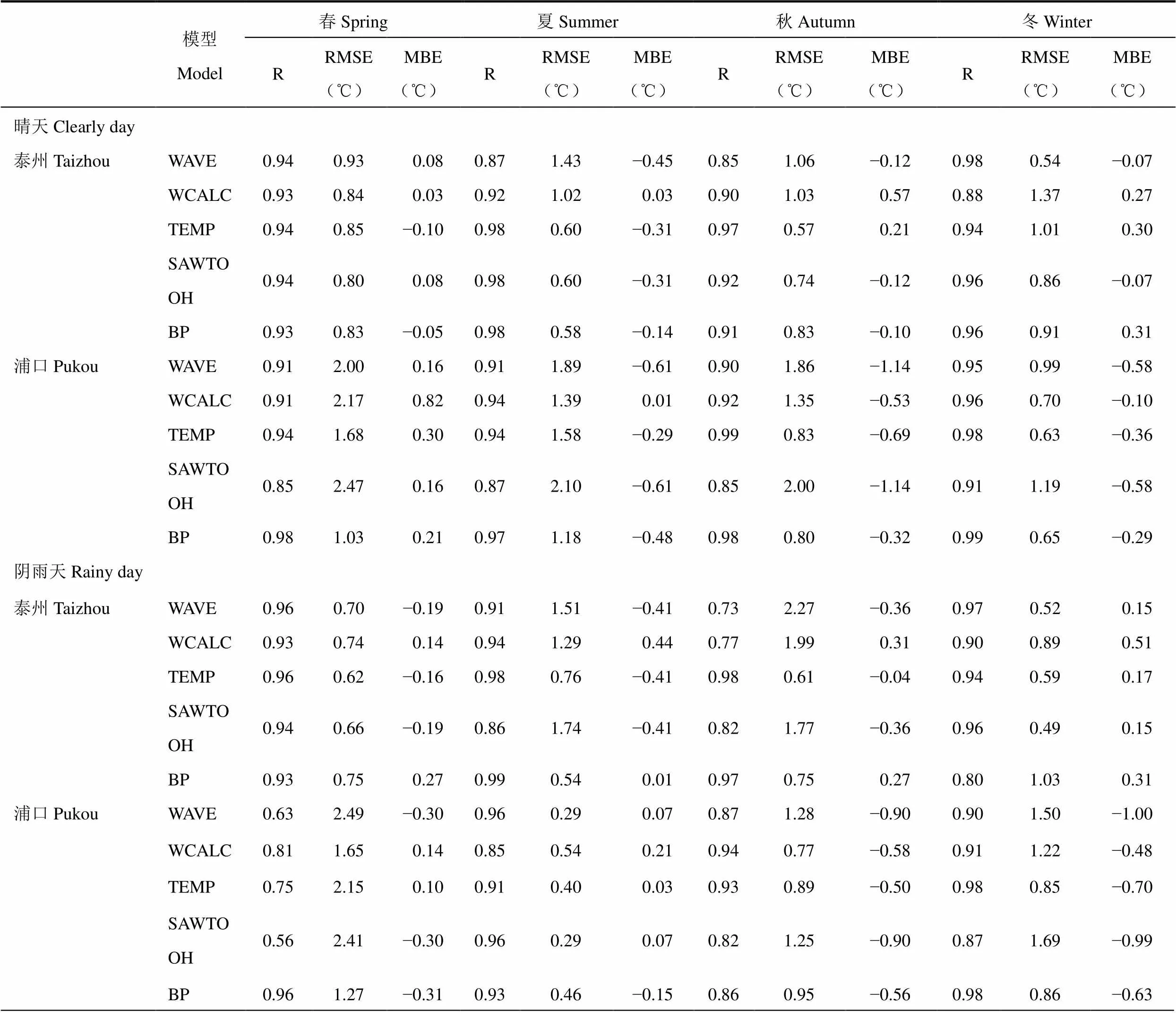
表5 四季典型天气条件下五种模型对玻璃温室内逐时气温模拟精度

3 结论与讨论

利用余弦分段函数（WAVE）、正弦分段函数（WCALC）、正弦−指数分段函数（TEMP）、一次分段函数（SAWTOOH）和神经网络模型（BP）5种模型对江苏省句容、盘城、泰州、浦口4个地区2个塑料大棚和2个玻璃温室内逐时气温进行模拟，对模拟结果与实测值之间相关性、均方差的比较表明，5种模型均可以通过当天的最高、最低气温模拟逐时气温变化，其中BP模拟精度较高且受温室类型、天气状况和季节变化的影响较小，普适性较高；TEMP模拟效果最好，且受天气和季节的影响较小，但其受温室本身特性和地区的影响较大；WAVE和WCALC模拟效果相近，对塑料大棚的模拟精度均远高于玻璃温室，SAWTOOH准确度较低且误差变化较大。

李倩等[16]所采用的谐波法和杨文刚等[13]所采用的逐步回归法均可以较好地模拟阴雨天和多云天气下温室气温的变化，但其在晴天的拟合结果较差。本研究所使用的方法在晴天和阴雨天均有良好的拟合结果。另一方面，以往研究对温室内气温的逐时模拟主要集中在利用室外的相关参数，如气温、相对湿度、辐射等数据反算出温室内的气温，建立在较长期的数学统计基础上，但是对于部分地区，室外的观测数据密集度较低，进行多种气象要素的密集观测较困难，而通常情况下会采用最高最低气温模拟室外气温变化[21]，造成一定的误差，所以这种方法也有一定的局限性。本研究使用日最高、最低气温模拟温室内逐时气温变化，所需要的数据量少，模拟精度较高，一定程度上可以弥补谐波法和逐步回归模型的缺点，提高温室气温模拟的精确度。

TEMP对温室逐时气温的模拟误差最小（RMSE=0.43℃），小于Reicosky等[18]对室外气温日变化模拟的结果（RMSE=2.08℃），表明温室内气温变化与室外气温变化相比更符合正弦−指数的变化模式。晴天条件下模拟结果与实际观测的相关性更好，阴雨天条件下较差，这是因为本研究采用的数学模型没有考虑到气温变化的连续性，一次连续的降温或者连续的升温过程通常情况下可以持续3d左右，以句容地区的温室大棚为例，2015年全年有29d的最低温出现在当日0：00−2：00。在气温连续变化的情况下，利用最高、最低气温模拟结果的准确度会受到影响。姜会飞等[20]在对室外气温进行模拟时，提出了正弦分段模拟法，这种方法对室外气温连续变化的模拟具有较高的准确度（RMSE＜0.7℃），朱业玉等[27]也提出了三段样条法对连续跃变的室外气温日变化进行模拟，也得到了较好模拟结果（RMSE＜1.31℃），这两种方法是否可以直接应用于温室气温逐时日变化的模拟还需进一步研究。本研究尚未考虑作物蒸腾作用对温室内气温的影响，这一点也需深入研究。

[1] 王琳,杨再强,杨世琼,等.高温与不同空气湿度交互对设施番茄苗生长及衰老特性的影响[J].中国农业气象,2017,38(12):761−770.

Wang L,Yang Z Q,Yang S Q,et al.Effects of high temperature and different air humidity on growth and senescence characteristics for tomato seedlings[J].Chinese Journal of Agrometeorology,2017,38(12):761−770.(in Chinese)

[2] 杨世琼,杨再强,王琳,等.高温高湿交互对设施番茄叶片光合特性的影响[J].生态学杂志,2018,37(1):57−63.

Yang S Q,Yang Z Q,Wang L,et al.Effect of high humidity and high temperature interaction on photosynthetic characteristics of greenhouse tomato crops[J].Chinese Journal of Ecology,2018,37(1):57−63.(in Chinese)

[3] Sharma P K,Tiwari G N,Sorayan V P S.Temperature distribution in different zones of the micro of a greenhouse:a dynamic model[J]. Energy Conversion & Mangagenment,1999,40:335−348.

[4] 张悦.日光温室冬季能量分配模型建立与能量分析[D].沈阳:沈阳农业大学,2016.

Zhang Y.Numerical modeling and energy distribution analysis of solar greenhuose in winter[D].Shengyang:Shengyang Agricultural University,2016.(in Chinese)

[5] 张芳,方慧,杨其长,等.基于CFD模型的大跨度温室自然通风热环境模拟[J].中国农业气象,2017,38(4):221−229.

Zhang F,Fang H,Yang Q C,et al.Ventilation simulation in a large-scale greenhouse based on CFD[J].Chinese Journal of Agrometeorology,2017,38(4): 221−229.(in Chinese)

[6] 任守纲,杨薇,王浩云,等.基于CFD的温室气温时空变化预测模型及通风调控措施[J].农业工程学报,2015,31(13):207−214.

Ren S G,Yang W,Wang H Y,et al.Prediction model on temporal and spatial variation of air temperature in greenhouse and ventilation control measures based on CFD[J].Transactions of the CSAE,2015,31(13):207−214.(in Chinese)

[7] 李石,张菁,张淑杰,等.沈阳地区日光温室内最低气温变化特征及其预报模型研究[J].气象与环境学报,2016,32(6):130−136.

Li S,Zhang J,Zhang S J,et al.Variation characteristics and forecasting models of the minimum temperature in solar greenhouse in Shenyang[J].Journal of Meteorology and Environment,2016,32(6):130−136.(in Chinese)

[8] 李瑞英,任崇勇.菏泽冬季日光温室内最低气温预测方法的对比研究[J].气象科学,2016,36(5):697−702.

Li R Y,Ren C Y.Comparative study on forecasting method of minimum temperature in solar greenhouse of Heze in winter[J].Journal of the Meteorological Sciences,2016,36(5): 697−702.(in Chinese)

[9] 李瑞英.菏泽冬季日光温室内气温预测[J].气象科技,2015,43(3):551−556.

Li R Y.Forecasting of air temperature in solar greenhouse of Heze in winter[J].Journal of the Meteorological Sciences,2015,43(3):551−556.(in Chinese)

[10]李宁,申双和,黎贞发,等.基于主成分回归的日光温室内低温预测模型[J].中国农业气象,2013,34(3):306−311.

Li N,Sheng S H,Li Z F,et al.Forecast model of minimum temperature inside greenhouse based on principal component regression[J].Chinese Journal of Agrometeorology,2013,34(3):306−311.(in Chinese)

[11]李国师,王海东,杨守邦,等.日光温室最低气温的预测与调控[J].中国农业气象,1994,15(6):26−28.

Li G S,Wang H D,Yang S B,et al.The forecast and regulation of minimum temperature in solar greenhouse[J].Chinese Journal of Agrometeorology,1994,15(6):26−28.(in Chinese)

[12]李德,张学贤,祁宦,等.宿州日光温室内部最高和最低气温的预报模型[J].中国农业气象,2013,34(2):170−178.

Li D,Zhang X X,Qi H,et al.Forecast model of the highest and lowest temperature in the sunlight greenhouse in Suzhou[J].Chinese Journal of Agrometeorology,2013,34(2):170−178.(in Chinese)

[13]杨文刚,孟翠丽,胡幼林,等.春季不同结构温室气温变化特征及预测模型[J].江苏农业科学,2015,(6):386−390.

Yang W G,Meng C L,Hu Y L,et al.Variation characteristics and prediction model of greenhouse temperature in different structures in spring[J].Jiangsu Agricultural Sciences,2015,(6):386−390.(in Chinese)

[14]刘淑梅,薛庆禹,黎贞发,等.基于BP神经网络的日光温室气温预报模型[J].中国农业大学学报,2015,20(1):176−184.

Liu S M,Xue Q Y,Li Z F,et al.An air tenperature perdict model based on BP neural networks for solar greenhuose in North China[J].Journal of China Agricultural University,2015,20(1):176−184.(in Chinese)

[15]金志凤,符国槐,黄海静,等.基于BP神经网络的杨梅大棚内气温预测模型研究[J].中国农业气象,2011,32(3): 362−367.

Jin Z F,Fu G H,Huang H J,et al.Simulation and forecast of air temperature inside the greenhouse planted myica rubra based on BP neural network[J].Chinese Journal of Agrometeorology,2011,32(3):362−367.(in Chinese)

[16]李倩,申双和,陶苏林,等.基于谐波法的塑料大棚内气温日变化模拟[J].中国农业气象,2014,35(1):33−41.

Li Q,Sheng S H,Tao S L,et al.Simulation of daily air temperature inside plastic greenhouse based on harmonic method[J].Chinese Journal of Agrometeorology,2014,35(1):33−41.(in Chinese)

[17]朱佳敏,杨栋,郭建民,等.南方双膜塑料大棚内气温的谐波模拟[J].中国农学通报,2017,33(9):133−140.

Zhu J M,Yang D,Guo J M,et al.Harmonic simulation of air temperature in double membrane greenhouses in south China[J].ChineseAgricultural Science Bulletin,2017,33(9):133−140.(in Chinese)

[18]Reicosky D C,Winkelman L J,Baker J M,et al.Accuracy of hourly air temperatures calculated from daily minima and maxima[J].Agricultural and Forest Meteorology,1989,46:193−209.

[19]余卫东,汤新海.气温日变化过程的模拟与订正[J].中国农业气象,2009,30(1):35−40.

Yu W D,Tang X H.Simulation and modification of daily variation of air temperature[J].Chinese Journal of Agrometeorology,2009,30(1):35−40.(in Chinese)

[20]姜会飞,温德永,李楠,等.利用正弦分段法模拟气温日变化[J].气象与减灾研究,2010,33(3):61−65.

Jiang H F,Wen D Y,Li N,et al.Simulation of the daily change of temperature by sine subsection method[J].Meteorology and Disaster Reduction Research,2010,33(3):61−65.(in Chinese)

[21]徐凡,马承伟.温室环境分析中冬季室外气温日变化及数学表达[J].农业工程学报,2013,29(12):203−209.

Xu F,Ma C W.Daily change and math-expression method of outside temperature in winter for greenhouse environmental analysis[J].Transactions of the CSAE,2013,29(12):203−209.(in Chinese)

[22]吴敏,孙军波,徐文文,等.慈溪地区日光温室气温变化规律[J].农学学报,2013,3(7):30−32,56.

Wu M,Sun J B,Xu W W,et al.Change laws of air temperature in solar greenhouse in Cixi[J].Journal of Agriculture,2013,3(7):30−32,56.(in Chinese)

[23]Det W C T.Simulation of assimilation, respiration and transpiration of crops[J].Agricultural Systems,1982,9(1):74−75.

[24]Wilkerson G G,Jones J W,Boote K J,et al.Modeling soybean growth for crop management[J].Transactions of the ASAE,1983,26:63−73.

[25]Parton W J,Logan J A.A model for diurnal variation in soil and air temperature[J].Agricultural Meteorology,1981,23:205−216.

[26]Ferreira P M,Faria E A,Ruano A E.Neural network models in greenhouse air temperature prediction[J].Neurocomputing,2002,43(4):51−75.

[27]朱业玉,宋丽莉,姬兴杰,等.基于分段三次样条函数逐时气象资料模拟方法研究[J].气象与环境学报,2017,33(2):44−52.

Zhu Y Y,Song L L,Ji X J,et al.Modeling method of hourly meterorological data based on piecewise cubic spline function[J].Journal of Meteorology and Environment,2017,33(2):44−52.(in Chinese)

Simulation Model of Hourly Air Temperature inside Glass Greenhouse and Plastic Greenhouse

WEI Ting-ting1, YANG Zai-qiang1,2, WANG Lin1, ZHAO He-li1, LI Jia-shuai1

(1. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science & Technology, Nanjing 210044, China; 2. Jiangsu Provincial Key Laboratory of Agrometeorology, Nanjing 210044)

In 2014−2016, plastic greenhouses and glass greenhouses in different districts of Jiangsu Province were selected for monitoring. Cosine segmentation function, sinusoidal piecewise function, sine-exponential piecewise function, first-order function and neural network model were used to simulate inside hourly temperature in different seasons and different weather conditions (clear day and rainy day). The results showed that all five models can simulate hourly air temperature inside greenhouse through the highest and lowest temperature of the day. The neural network simulation accuracy was the higher (RMSE=0.69℃) and was less affected by the type of greenhouse, weather conditions, and seasonal changes, the universality was higher. The sinusoidal-exponential piecewise function had the best accuracy (RMSE=0.43℃) and was less affected by weather and seasons, but it was affected by the characteristics of the greenhouse itself and the region. The cosine piecewise function (RMSE=0.8℃) and the sinusoidal function (RMSE=0.78℃) had similar simulation results and was affected by the weather and region. The accuracy of a piecewise function is low (RMSE=0.90℃) and the error varies greatly. Models had higher simulation accuracy in plastic greenhouses then it in glass greenhouses. Seasonal variation of the model's simulation accuracy was different between the models and the types of greenhouse, but usually, the simulation error in spring and winter was greater than in autumn, and the error in summer was the smallest.

Plastic greenhouse;Glass greenhouse; Simulation of air temperature；Greenhouse；Daily variation of temperature

2018−03−01

。E-mail：yzq@nuist.edu.cn

国家自然科学基金面上项目（41775104）；江苏省科技支撑计划社会发展项目（BE2015693）；2018年度江苏省研究生科研创新计划（KYCX18_1028）

韦婷婷（1996−），女，研究方向为设施农业气象。E-mail：2843717682@qq.com

10.3969/j.issn.1000-6362.2018.10.003

韦婷婷,杨再强,王琳,等.玻璃温室和塑料大棚内逐时气温模拟模型[J].中国农业气象,2018,39(10):644−655