线性代数课程中的特征值与特征向量教学研究*
刘智慧 付丽华 李宏伟 李超群
(中国地质大学数理学院,湖北 武汉 430074)
特征值与特征向量是《线性代数》中的重点内容之一,在众多领域有着广泛的应用[1-8].“特征”一词来自德语的eigen,翻译为“自身的”“有特征的”“特定于……的”,强调了特征值与特征向量对特定矩阵的重要性. 由于特征值与特征向量涉及的概念、定理较为抽象,在一定程度上阻碍了学生对其理解与认识. 如果在特征值与特征向量教学中,融入几何直观并通过实际生活中的具体例子阐明特征值与特征向量的作用,将在一定程度上调动学生的学习积极性,使其更好地掌握特征值与特征向量. 本文借助MATLAB软件从几何直观以及出租车调配和高维数据降维的具体实例说明特征值与特征向量,注重应用特征值与特征向量解决实际中的相关问题,加强学生对特征值与特征向量的深入理解,领会特征值与特征向量的数学意义和应用价值.
1 矩阵的特征值与特征向量
定义1[7, 9]设A为n阶矩阵,x为非零向量,若存在数λ,使得
Ax=λx
成立,则称λ为A的特征值,x为A的属于λ的一个特征向量.
从定义1可知,特征向量为一些特定的向量,这些向量在方阵A的作用下保持方向不变,只进行长度上的伸缩(当λ<0时,伸缩值为负值;当λ=0时,伸缩值为零). 若x为A的特征向量,则kx(k≠0)也是A的特征向量,所以特征向量不是一个向量而是一个向量族.
定理1特征值分解定理[7, 9]设A为n阶对称矩阵,则必存在一个正交矩阵P=[p1,p2,…,pn],使得
A=PΛPT
其中,(·)T表示转置运算,Λ=diag{λ1,λ2,…,λn},λi为A的特征值,pi为A的属于λi的特征向量.
从定理1中可知,任意一个实对称矩阵总可以用它的特征值和特征向量完全描述.
通过一个具体的例子演示矩阵的特征值和特征向量.
利用MATLAB命令求出矩阵的特征值和特征向量,相应的MATLAB程序为:
A=[1 0;0 2];
[P,D]=eig(A);%求矩阵A的特征值和特征向量
eigshow(A);%演示矩阵A的特征值和特征向量
例1的MATLAB程序运行结果如下:
P=
1 0
0 1
D=
1 0
0 2
图1描述了蓝色向量Ax随绿色向量x的变换关系,x表示二维单位向量,当用鼠标拖动x围绕原点旋转时,Ax随着x旋转,向量x的轨迹是一个绿色单位圆,向量Ax的轨迹为一个蓝色椭圆. 在图1中,当x旋转到水平方向和竖直方向时(见图1(c)(d)),Ax恰好与x重合,即Ax=λx,由定义1知,矩阵A的两个特征值为椭圆的短轴和长轴,对应的特征向量分别为k1(1,0),k2(0,1),其中k1≠0,k2≠0. 例1说明,对所有二维向量,只有形如k1(1,0)和k2(0,1)的二维向量在二阶对角矩阵A的作用下保持方向不变.
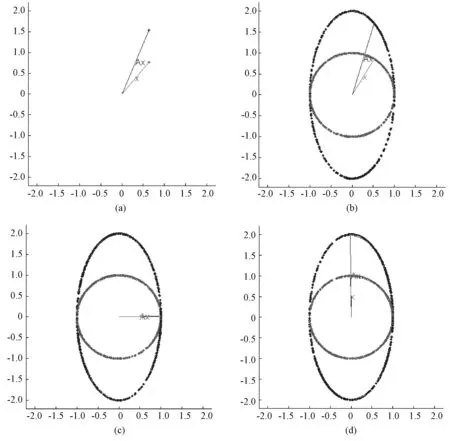
图1 矩阵特征值和特征向量的图形演示
2 特征值与特征向量的应用
2.1 出租车的调配问题
假设一家出租车公司在甲地和乙地各有一家分支机构,专门负责为旅游公司提供出租车. 由于甲地和乙地距离不远,出租车每天可以往返两地. 根据公司统计的历史数据,每天甲地的车辆有60%前往乙地后返回甲地,余下40%前往乙地并留在乙地分支机构;而每天乙地的车辆有70%前往甲地后返回乙地,余下30%前往甲地并留在甲地分支机构. 假设出租车公司出租车数量是固定不变的,问:当经过足够长时间后,甲地和乙地出租车数量是否会越来越不平衡?如果甲乙两地车辆数量不平衡,公司如何调配?
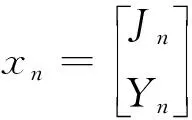
(1)
式(1)用矩阵表示为
≜Axn.
(2)
利用MATLAB命令求出矩阵A的特征值为λ1=1,λ2=0.3,对应的特征向量为p1=[-0.600 0,-0.800 0]T,p2=[-0.707 1,0.707 1]T.
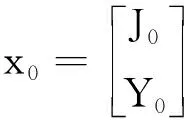
又pi为特征向量,故xn=Anx0=c1(λ1)np1+c2(λ2)np2. 若n→∞,则(λ2)n=(0.3)n→0. 于是,当c1>0时,
xn≈c1(λ1)np1,
(3)
以及
xn+1≈c1(λ1)n+1p1=λ1c1(λ1)np1≈λ1xn.
(4)
式(3)表明,xn的2个分量之比(甲地和乙地出租车的数量之比)近似等于p1对应分量之比,即甲乙两地出租车的数量之比只与最大特征值λ1=1对应的矩阵特征向量p1有关,而与甲乙两地初始
出租车的数量x0无关. 由于p1分量之比为一个常数,所以当经过足够长时间后,甲地和乙地出租车数量之比趋于一个稳定数,即甲乙两地车辆数量趋于平衡. 式(4)表明,xn最终以近似λ1的倍数增长,故矩阵A的最大特征值λ1确定了最终增长率.
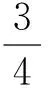
以上例子说明,利用矩阵的特征值和特征向量,选择矩阵较大特征值及对应的特征向量可以分析出租车的调配问题.

图2 甲地和乙地出租车数量之比
矩阵A的特征值和特征向量及图2(a)相应的MATLAB程序为:
A=[0.6 0.3;0.4 0.7];
x0=[2 000;5 000];
[P,D]=eig(A);
fori=1∶30
x(:,i)=A^i*x0;
end
plot(x(1,:)./x(2,:));
xlabel(′n/天数′);
ylabel(‘甲地车辆与乙地车辆之比’);
2.2 高维数据的降维问题
现有m组数据,每一组数据为n维向量,在机器学习中,若对这n维m组数据点直接进行分析和挖掘,那么算法的复杂度往往与维数n呈指数级关系. 能否将n维向量组降为k维向量组(k 将此数据看作n×m的矩阵Xn×m,欲使n维向量组降为k维向量组,即寻找矩阵Pk×n,使得Pk×nXn×m=Yk×m,则矩阵Yk×m为降维的k维向量组. 下面用简单的例子说明基于矩阵特征值和特征向量的高维数据降维问题. 图3(a)表示五个不同的二维数据点,若将此数据点向x轴投影,则右边的两个点会重叠在一起,中间的两个点也会重叠在一起,于是五个不同的二维数据点投影后只剩下三个不同的投影值,这是一种严重的信息丢失. 同理,若将此数据点向y轴投影,则投影后也只有三个不同的投影值. 因此x轴和y轴不是数据点最好的投影方向. 但若将此数据点向通过第一象限和第三象限的斜线投影(见图3(b)),则五个二维数据点投影后为五个不同的投影值,即数据点向该斜线投影后,二维数据点降为了一维数据点,同时保留了五个原始数据信息. 此例说明,将高维数据进行降维,只需将数据点向某些方向进行投影,使得在这些方向上的投影值尽可能分散,问:如何找到这些投影方向? 图3 二维数据点分布情况 显然,A为对角矩阵,A对角元表示二维向量的方差(刻画分散程度);A对角元外的元素表示维度间的协方差(刻画维度间的不相关性). 对五个数据点进行降维,同时尽可能保留五个原始数据点,即满足五个数据点投影后投影值尽可能分散(二维向量的方差尽可能大),同时维度间尽可能不存在相关性(维度间的协方差尽可能小),即使得协方差矩阵A对角化(对角元的元素从大到小排列,对角元外的元素为零). (5) =[-2.121 3,-0.707 1,0,0.707 1,2.121 3]. 其中,y为降维后的五个一维数据点,p1为二维数据点的投影方向(见图3(b)). 二维数据点降为一维数据点的相应MATLAB程序为: X=[-2 0 0 1 1;-1 -1 0 0 2]; A=(1/5)*X*X′; %数据点的协方差矩阵A [P,D]=eig(A); y=P(:,1)′*X; %降维后的一维数据点 以上例子说明,矩阵较大特征值对应的特征向量上包含了较多的信息量,利用矩阵前面部分较大特征值对应的特征向量可实现高维数据的降维. 本文对《线性代数》课程中特征值和特征向量两个抽象的概念运用MATLAB软件,从几何直观演示、出租车的调配及高维数据降维等实际问题进行了阐述,使得学生能更好地理解和认识特征值与特征向量,同时,对学生的学习兴趣及学生运用数学知识解决实际问题的能力的培养有一定的帮助.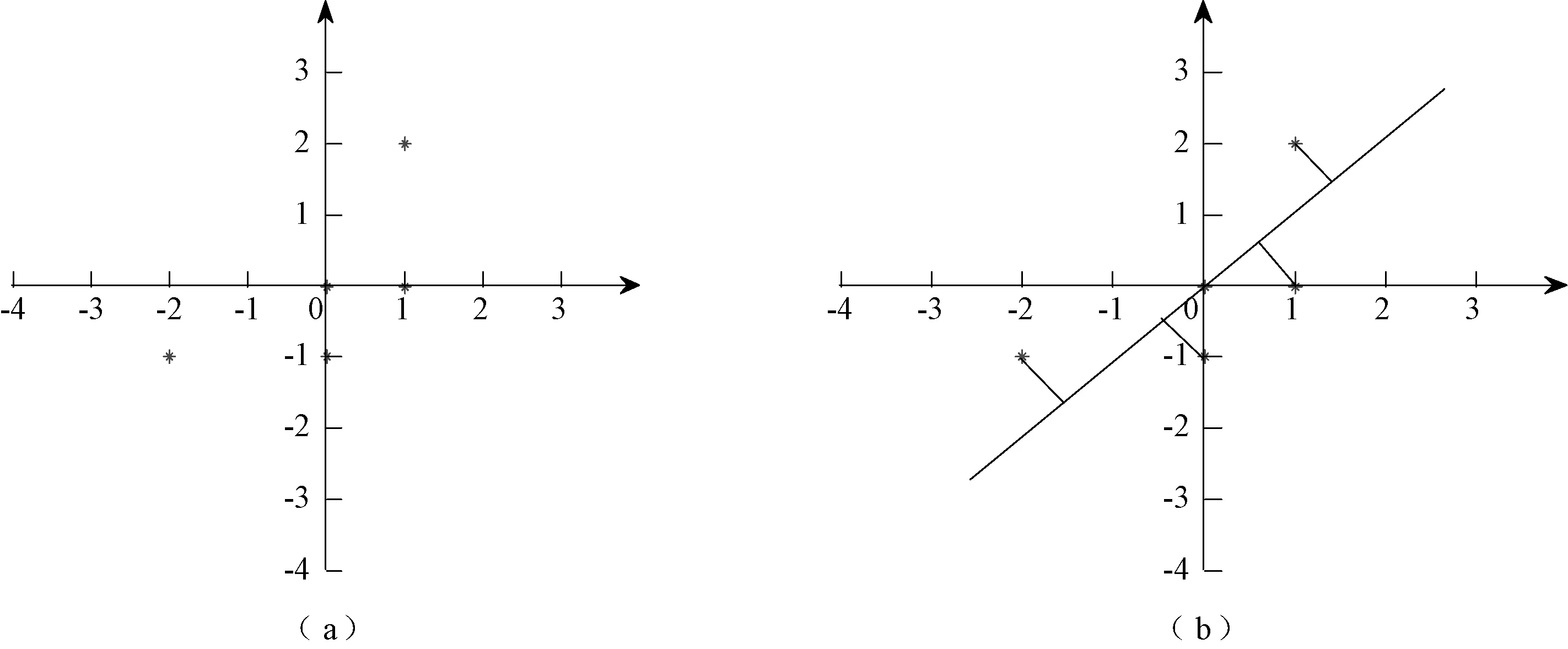
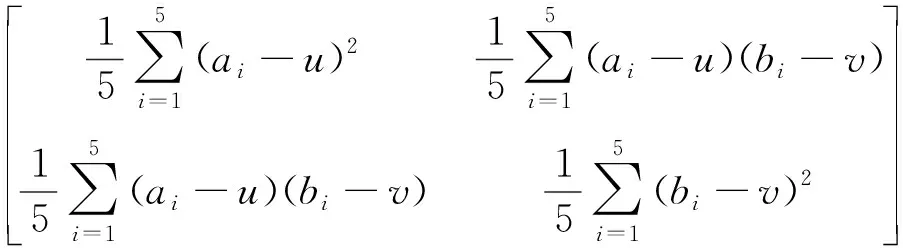
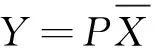


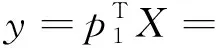

3 小 结

