交通荷载路径下超固结软黏土变形特性研究

，，

(1.温州市铁路与轨道交通投资集团有限公司, 浙江 温州 325000； 2.哈尔滨工业大学(深圳) 土木与环境工程学院, 广东 深圳 518000)

1 研究背景

我国沿海地区及邻近内陆城市广泛分布着软黏土地层。近些年来，随着经济不断繁荣发展、交通设施迅速发展，我国高速铁路、高速公路、城市地铁、市政道路拥有量位于世界前列，并且将会长期处于高速发展期。这些交通设施在运营期间，由于长期受到交通荷载作用，路基沉降问题导致的道路安全性和适用性降低，一直是工程界关注的重点和难点。

对于交通荷载下路基土体特性试验研究，目前国内外已有大量研究成果，研究方法主要集中在动三轴系统和空心圆柱扭剪系统。①利用动三轴系统：Parr[1]以伦敦软黏土为研究对象，建立了累积塑性应变速率与循环次数的关系模型；Monismith等[2]建立了在循环荷载下饱和软黏土累积应变的指数型模型；Li等[3]通过一系列试验，考虑了动偏应力、静强度等因素对Monismith模型提出修正；刘国清等[4]研究了超固结比对交通荷载下软黏土变形特性影响；刘添俊等[5]进行了交通荷载下正常固结饱和软黏土累积应变速率研究；郭林等[6]进行了交通荷载下回弹应变和累积变形特性试验研究；刘新峰等[7-8]进行了交通荷载作用下超固结软黏土地基长期沉降研究；张涛[9]进行了地铁荷载下不同固结度软黏土沉降研究；王军等[10]对交通荷载作用下超固结软黏土孔压-软化模型进行了研究。② 利用空心圆柱扭剪系统：沈扬等[11]进行了小角度主应力轴循环旋转应力路径下超固结软黏土性状试验研究；郭林[12]模拟交通荷载进行循环荷载下正常固结软黏土特性研究；肖军华等[13]研究主应力轴旋转对地铁荷载作用下正常固结软黏土累积变形的影响。

国内外利用动三轴系统进行的交通荷载下软黏土特性试验研究，其研究对象为正常固结和超固结软黏土。软黏土路基在实际交通荷载下所受到的主应力的方向是不断变化的，而动三轴系统只能施加轴向的循环荷载，主应力轴的方向始终是不变的，不能模拟主应力轴旋转的应力路径。空心圆柱扭剪系统由于同时施加循环的轴向应力和剪应力，可以模拟交通荷载下软黏土主应力轴旋转的应力路径，但目前针对交通荷载作用下的研究对象均为正常固结软黏土。在实际工程当中，由于地面挖方或者超载预压等地基处理作用，地基都存在或多或少的超固结性。目前，尚未开展利用空心圆柱扭剪系统进行交通荷载下超固结软黏土的研究。

本文利用GDS空心圆柱扭剪系统模拟交通荷载，对不同超固结比饱和软黏土进行不排水循环加载试验，研究超固结比对交通荷载作用下饱和软黏土特性的影响。以期进一步完善交通荷载作用下饱和软黏土室内试验，为工程施工设计提供参考。

2 土样制备和试验仪器

2.1 土样制备

土样采用温州地区软黏土。制作步骤为：

(1)将原状黏土切割成为体积不超过200 cm3、最大边长不超过10 cm的黏土块，放置于温度为100 ℃的烘箱中，烘干时间≥48 h，保证黏土块的自由水基本上完全散失。烘干之后，密封保存，以免从空气中吸收水分而变潮，影响粉碎效果。

(2)用粉碎细度为50～200目的粉碎机将烘干的黏土块进行粉碎，为保证粉碎效果，每次粉碎的质量不超过2 kg。将粉碎的土粉用振动筛进行筛析，振动筛孔径为0.3 mm，筛析剩下的粗颗粒不再使用，以保证制取试样的均匀性，筛析得到的土粉要密封保存。

(3)称量振动筛筛析得到的土粉23 kg，清水18.4 kg，配备含水率为80%的泥浆，先用手将土粉和水充分混合，再用打浆机将泥浆搅拌均匀，以无手感可触的颗粒为搅拌符合要求。

(4)将配置的泥浆通过漏斗倾倒在高压固结仪里面，泥浆上下底层分别摊铺一块透水石，砝码通过杠杆、圆盘施加压力至透水石，对泥浆进行分级加载，通过3种分级荷载(12.52550 kPa, 12.5255075 kPa,12.5255075100 kPa)分别制取50，75，100 kPa荷载下的重塑软黏土饱和土样。

表1 重塑土样基本物理性质指标Table 1 Physical properties of remolded test soil

2.2 试验仪器

试验仪器采用GDS空心圆柱扭剪仪，可以施加独立控制的内围压(Pi)和外围压(Po)以及自定义波形的轴力和扭矩，扭矩的存在可以通过施加剪应力实现主应力轴的旋转(最大主应力与竖直方向角度不断变化)，该应力路径可以很好地模拟真实情况下的交通荷载。

3 试验方案

3.1 加载方案

将制备好的试样用切土器制作成高200 mm，外直径100 mm,内直径60 mm的空心圆柱体。首先将制取好的空心圆柱试样装入空心圆柱扭剪仪里进行反压饱和，用B(孔压系数)值检测试样饱和度，当B值>0.98的时候，认为试样已经完全饱和。饱和完成之后进入固结阶段，将50，75，100 kPa下制得的重塑土样均在50 kPa内外围压下各向同性固结，当试样每小时排水量<100 mm3视为固结完成，这样就形成了正常固结土(超固结比OCR=1.0)和超固结比为1.5和2.0的超固结土。最后一个阶段为循环荷载加载阶段，加载过程当中内外围压始终保持为50 kPa，关闭反压器开关以及排水阀门，进行不排水循环加载试验。

图1 某城市地面轨道路线数值分析模型及计算结果Fig.1 Numerical analysis model and results of urban rail line

3.2 加载波形

为获得交通荷载作用下路基土体单元所受的动应力，笔者曾对某城市地面轨道路线进行了数值计算[14]，见图1。轨道采用60 kg/m型钢轨，横截面尺寸为15.3 cm×7.8 cm；混凝土轨枕长2.6 m，间距0.6 m。为减小边界效应的影响，地基模拟范围为60 m×60 m。图1(a)为剖分网格后的几何模型。图1(b)为轮载分布示意图，列车轴重采用250 kN，相应单轮轮重125 kN。路基层参数选择见文献[14]。图1(c)为数值分析计算得到的路基单元体所受的应力路径，其中横坐标为移动荷载到单元体距离y与轮轨长度L的比值，σz为竖向应力；σy为水平应力。可以看出，交通荷载作用下，土单元体上的竖向偏应力由0增加到峰值再减小到0，而剪应力的方向会产生变化，从而造成主应力轴旋转。

本试验对试样同时施加循环轴向应力和循环剪应力，用以模拟图1(c)中的土单元体应力路径，加载频率均为1 Hz。本研究共设计了4种不同荷载下的循环加载试验，共计12个，详见表2。

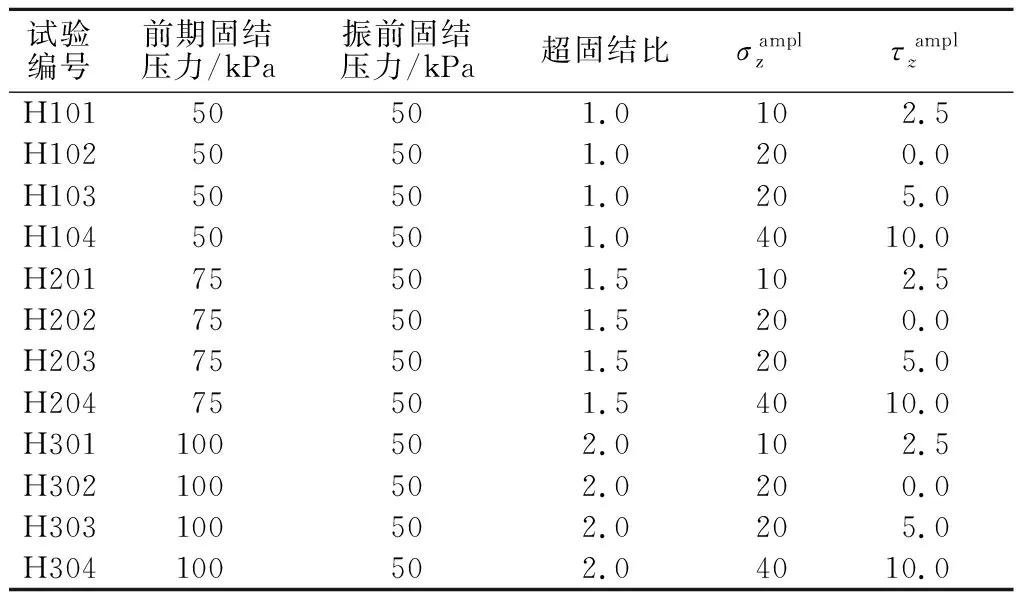
表2 试验加载方案Table 2 Schemes of loading test

4 试验结果

4.1 应力路径分析

图2 主应力轴旋转应力路径Fig.2 Rotation stress path of principal stress axes

实际交通工程当中随着车轮的移动会产生剪应力，造成主应力轴的旋转。图2为空心圆柱扭剪仪模拟出的交通荷载的应力路径。由于施加循环剪应力，广义偏应力q，大主应力方向和垂直方向的夹角α都在不断发生变化，与只能施加循环轴向应力，主应力轴方向始终不变的GDS动三轴系统相比，更符合交通荷载的实际情况。

4.2 典型试验结果分析

试样在循环加载过程中的应变由2部分组成:一部分是随循环次数不断增长的不可恢复的累积应变z,p;另一部分是在卸载过程中可恢复的回弹应变εz,r。为更清楚地表达各个应变分量之间的关系，绘出循环荷载下的应力-应变关系曲线，见图3。各应变之间的关系公式εz=εz,p+εz,r。为研究循环荷载下软黏土的回弹模量，将其定义为MZ[12],计算式为

式中σampl为竖向动应力。

图3 循环荷载下应变发展曲线Fig.3 Curves of strain development under cyclic loading

4.3 超固结比OCR对软黏土应变发展的影响

图4为不同超固结比软黏土累积应变发展曲线，CSR为循环应力比。图4(a)中正常固结土在经历10 000次循环后产生了0.055%的累积应变，而超固结比为1.5和2.0的超固结土分别产生了0.035%和0.017%的累积应变，产生的累积应变分别为正常固结土的64%和31%。对于超固结比为1.5和2.0的超固结土来说，10 000个循环荷载结束时累积应变基本上已经趋于稳定;而正常固结土在10 000个循环结束之后累积应变还未达到稳定，随着循环次数的加大，累积应变的差异会更大。上述结果说明超固结作用可以限制土体累积应变的发展，促进累积应变达到稳定，且超固结比越大，作用越明显。

图4 不同超固结比软黏土累积应变发展曲线Fig.4 Curves of accumulated strain development under different over-consolidation ratio

将图4(b)与图4(a)比较可以看到，当荷载增加时，在10 000个循环荷载结束之后，无论是正常固结土还是超固结土，软黏土的累积应变均没有达到稳定，说明荷载越大，软黏土在循环荷载下达到稳定所需的循环次数越大。图4(c)中，正常固结土和超固结比为1.5的超固结土在循环开始时应变近似呈直线急速增长且快速达到破坏，而超固结比为2.0的超固结土在经历10 000次循环过后累积应变仅在0.3%左右，说明超固结作用可以提高土体的强度。将图4(c)与图4(a)、图4(b)相比较可知,荷载越大，超固结比对累积应变的影响越明显。这些现象表明，经超载预压地基处理后，软黏土抵抗变形的能力有所增加，相同动应力水平下处理后路基沉降将明显减小。

图5 不同超固结比软黏土应力-应变滞回曲线(CSR = 0.4, η = 0.25)Fig.5 Curves of stress-strain hysteresis loop development under different over-consolidation ratio (CSR = 0.4, η = 0.25)

4.4 超固结比对软黏土应力-应变滞回曲线和回弹模量的影响

图5为不同超固结比软黏土在循环荷载作用下的应力-应变滞回曲线，N为剪切应力与竖向应力之比。图5中的(a),(b)，(c)试样超固结比分别为1.0，1.5，2.0，应力路径均为CSR=0.4，η=0.25。将循环次数N为10，100, 1 000，10 000时的初始应变归零对不同循环次数下的应力-应变滞回曲线进行对比。图5中，无论是超固结土还是正常固结土，当循环次数增加的时候，应力-应变滞回曲线均朝向应变轴的方向倾斜，且应力-应变滞回曲线包围的面积越来越小，说明随着循环次数的增加，无论是正常固结土还是超固结土，土体的软化程度不断加强，且土体变形越来越以弹性应变为主。

从图5中还可看出，在循环次数一定时，当超固结比增大时，产生的轴向应变减小，比如在第10次循环荷载作用下，正常固结土产生了0.068%的轴向应变，而超固结比为1.5和2.0的超固结土分别产生了0.062%和0.054%的轴向应变，说明软黏土变形模量随着超固结比的增加而增加。此外，在循环次数一定时，应力-应变滞回圈的面积也随着超固结比的增大而减小，即卸载阶段的滞回曲线和加载阶段的滞回曲线更接近，说明随着超固结比的增大，软黏土的黏塑性特征越来越不明显，弹性特征越来越占主要部分。

另外，正常固结土在不同循环次数下的应力-应变滞回曲线和超固结土相比就比较离散，且超固结土在较小的循环次数下就可以达到稳定，表明超固结土的软化速率要低于正常固结土。图5中的(b)和(c)的应力-应变滞回曲线的差别远没有图5中的(a)的应力-应变滞回曲线的差别大，说明超固结比越大，超固结比的增加对土特性的影响越小。

图6为10 000个循环之后不同荷载下回弹模量随超固结比的变化趋势，可以看到，虽然回弹模量随着超固结比的增大而增大，但是增大的速率却在降低，超固结比越小时，超固结比的增加对土体回弹模量的增加更明显。

图6 不同超固结比下回弹模量对比Fig.6 Comparison of modulus of resilience under different over-consolidation ratio

5 结 论

利用GDS空心圆柱扭剪仪模拟交通荷载，对不同超固结比重塑软黏土展开不排水条件下的循环加载试验，研究超固结比对交通荷载下软黏土累积应变、应力-应变滞回曲线、回弹模量的影响，得到以下结论：

(1)在交通循环荷载下，当循环次数相同时，软黏土孔压随超固结比的增大而减小。表明经超载预压地基处理后，相同动应力水平下软黏土软化程度将有所降低。

(2)在交通循环荷载下，当循环次数一定时，超固结比越大，土体累积应变越小，且超固结比越大，土体累积应变达到稳定所需的循环次数越小。表明在交通荷载下，当通过的车辆次数一定时，路基软黏土在经过超载预压地基处理后，路基沉降会大大降低。

(3)在交通循环荷载下，超固结比越大，应力-应变滞回曲线随循环次数的变化越不明显，应力-应变滞回曲线越集中，土体随循环次数的软化程度越弱，弹性越明显。当循环次数相同时，超固结比越大，应力-应变滞回曲线朝应变轴倾斜的程度越小，土体的回弹模量越大。且超固结比越小，超固结比的增加对回弹模量的增加越明显。