暴雨强度公式对比分析及参数优化求解

，

(四川水利职业技术学院 水利工程系，四川 都江堰 611830)

1 研究背景

随着全球气候变化和我国城市建设快速发展，近年来我国各大城市洪涝灾害日趋严重，城市洪涝灾害已成为制约当地社会经济发展的突出问题[1-2]。暴雨强度公式是确定城市防洪除涝或者排水工程设计标准的重要依据，其选择的合理性直接影响工程的规模和效益，也直接影响着工程投资建设进度[3]。

暴雨强度公式为超定非线性方程，其参数估计是非线性优化问题，参数率定在实际工作中十分重要，是近年来城市水文学领域的研究热点，受到人们的广泛重视。近几年，随着暴雨资料的积累，各地区不断采用新方法对暴雨强度公式参数进行拟合，大部分城市编制并发布了适用于当地的暴雨强度公式参数[4-5]。国内相关研究主要集中在市政行业暴雨强度公式的拟合方法的选择，以及暴雨样本的选取。目前国内外学者从各个角度对暴雨强度计算进行了大量的研究：张子贤等[3]采用非线性回归方法，研究了市政行业暴雨强度公式的直接拟合法，使所求的误差平方和最小；郭渠等[6]通过不同的采样方式及多种曲线拟合，分析了重庆主城区暴雨强度公式的推算和应用；万永静等[7]用不同拟合方法推求了沭阳县的暴雨强度公式；周玉文等[8]对比研究了市政行业暴雨强度公式所选样本采用年最大值法和年多个样法对设计暴雨值的影响；倪长健等[9]等分析了免疫进化算法及其在暴雨强度公式参数优化中的作用等。中国水利行业和市政行业发布实施的相关规范均对暴雨强度公式进行了详细的说明，水利行业相关标准规范如各地的中小流域设计洪水手册等；市政行业相关标准规范如《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》[10]、《室外排水设计规范》[11]等。

本文以自贡气象站为研究对象，对比分析了水利行业和市政行业暴雨强度公式计算过程的差异，在此基础上建立基于SCE-UA(Shuffled Complex Evolution)优化算法的参数求解方法，研究了2种暴雨强度公式对设计暴雨成果的影响,以期指导各地区水利工程和市政工程选择合适的暴雨强度公式。

2 暴雨强度计算方法对比分析

2.1 暴雨资料选样方法

暴雨资料的选样是从降雨资料中选择一定数量的雨样作为样本。常用的选样方法有年最大值法、年多个样法和年超大值法。

我国水利行业暴雨资料选样一般采用年最大值法，即从历年各历时的暴雨统计资料中仅选取指定历时的最大一组雨量，组成年最大暴雨样本系列，作为“年最大值法”暴雨强度公式的统计样本系列[12]。进行暴雨频率分析计算时，暴雨资料年限需要30 a以上。水利行业在计算小流域设计洪水时采用的暴雨历时一般为1/6，1，6，24 h共4种降水历时。水利行业的设计重现期较大，如十年一遇、百年一遇等。

我国市政行业暴雨资料的选样方法以往多采用年多个样法，即从每年各历时的雨量资料中选取4～8个最大值雨量，然后取雨量资料年限系列长度的3～4倍，组成年最大暴雨样本系列，作为“年多个样法”暴雨强度公式的统计样本系列[13]。我国在20世纪80年代以前，各地区暴雨资料观测年限普遍偏短，短历时的暴雨资料更是严重不足[14]。由于短历时暴雨资料的年限一般仅有5～20 a，以往市政行业多采用年多个样法进行暴雨资料选样，其暴雨系列的长度将大于或者等于年限。最新出版的《室外排水设计规范》(GB 50014—2006)推荐采用年最大值法选取暴雨样本系列，资料年限至少需要30 a以上。市政行业采用的暴雨历时一般为5，10，15，20，30，45，60，90，120，150，180，360，1 440 min共13种降水历时。市政行业排水系统的设计重现期一般较小，如两年一遇、五年一遇等。

2.2 暴雨频率分布线型

我国水利行业暴雨频率分布线型常选用P-III分布。我国市政行业暴雨频率分布线型常选用P-III分布或Gumbel分布。P-III型分布的总体参数有较清晰的物理意义，多被水利行业和市政行业选为暴雨频率分布理论线型[15]。当无相关暴雨频率分布线型时，应进行多种暴雨频率分布线型函数的拟合试验，以拟合优度作为评价标准，从中选取拟合效果较好的理论频率曲线函数类型，当拟合精度差异不大时推荐采用P-III型分布函数[16]。

P-III型分布曲线是一端有限、一端无限不对称的单峰、正偏曲线。假定所研究的暴雨随机变量X服从P-III型分布，记作X～Γ(x；a，α，β)，其概率密度函数fx为

x≥a，α>0,β>0 。

(1)

式中：a为位置参数，即为洪水随机变量X的最小值；α为形状参数;β为尺度参数。

Gumbel分布是根据极值定理导出的，又称为极值分布，它实际上是P-III曲线的一个特例，即变差系数Cs取1.140；其频率分布形态为偏态铃形分布。

2.3 暴雨强度公式计算

暴雨强度公式是反映历时为t、频率为P或者重现期T下的平均暴雨强度。目前国内外采用的暴雨强度公式形式众多[17]，可归纳为

(2)

式中：i为设计平均暴雨强度；b为降水历时修正参数；A为雨力参数;n为暴雨衰减指数；t为设计暴雨历时。

我国水利行业暴雨强度计算的一般公式为

(3)

式中：i为历时t、频率P的平均暴雨强度(mm/h)；SP为历时t=1 h、频率为P的平均暴雨强度，简称雨力，数值上等于年最大1 h平均雨强(mm/h)；P为设计暴雨频率(%)；t的单位为h。

我国市政行业暴雨强度计算的一般公式为

(4)

式中：i为设计平均暴雨强度(mm/min)；C为雨力变动参数；b为降水历时修正参数(min)；T为设计暴雨重现期(a)；t的单位为min；A的单位为mm。

市政行业排水设计采用的雨水参数一般用体积(容量)来表达，暴雨强度q(L/(s·hm2))与i(mm/min)之间可以根据q=167i进行换算。

3 暴雨强度公式参数优化求解

3.1 目标函数

根据各历时暴雨样本系列，用数学期望公式(当样本系列中有特大值时，采用钱穆公式)计算经验频率，矩法初估参数，P-Ш型频率曲线拟合点据，目估适线分析确定统计参数，计算设计标准下各历时的暴雨设计值。

设暴雨强度公式中的参数共m个，记为θ=(θ1,θ2,…,θm)。根据同一设计频率P下的不同历时暴雨设计值(历时取10，20，30，60，90， 120，150，180，360，1 440 min共10种)，同时考虑到水利行业和市政行业的暴雨设计值多采用重现期较小和历时较大的实际情况，构造一种对数离差绝对值和最小准则(简称“LWAS准则”)作为暴雨强度公式参数优化求解模型的目标函数，其计算表达式为

式中：LWAS为LWAS准则目标函数值；θ为目标函数含有的参数，即暴雨强度公式的参数；IP,j为设计标准P下不同历时的暴雨设计值；iP,j(θ)为暴雨强度公式计算的暴雨强度-历时-频率关系曲线上的纵坐标值；k为历时个数。

我国《室外排水设计规范》(GB 50014—2006)中推荐的平均绝对均方根误差(简称“MAS准则”) 计算表达式为

(6)

式中MAS为准则目标函数值。

LWAS准则在暴雨历时较大时的拟合效果比MAS准则更优，同时亦能兼顾到暴雨历时小的资料，克服了传统MAS准则在历时较大时拟合效果差的缺点。

3.2 约束条件

暴雨强度公式参数优化为超定非线性回归方程，采用常见的方法求解该方程难度较大。一般来说，重现期越大、历时越短，其暴雨强度就越大，其求解的暴雨强度-历时-频率关系曲线(简称“IDF曲线”)在双对数坐标系中为下凹曲线[18]。暴雨强度公式参数与地方暴雨特性有密切关系，具有显著的区域性规律。暴雨强度公式参数以及平均暴雨强度参照《数值修约规则与极限数值的表示和判定》(GB/T 8170—2008)[19]的要求取舍有效数字。

通过分析全国各地区水文手册中暴雨强度公式，水利行业暴雨强度公式(3)中的参数SP和n的取值范围为：SP∈[1,10]mm/h，n∈[0,1]。

通过分析全国各城市给排水手册中暴雨强度公式，市政行业暴雨强度公式(4)中的4个参数的取值范围为：A∈[1,50]，C∈0,1，b∈[0,50]，n∈[0,1]。

3.3 优化算法

暴雨强度公式可采用符合数理统计基础的数学优化方法求解参数，包括求解非线性方程的方法和最优化方法率定暴雨强度公式参数。常用求解算法均存在计算效率低、易陷入局部解等问题。针对目标函数非线型和高维的特点，本文采用求解精度高和运行效率快的SCE-UA优化算法计算暴雨强度公式参数。SCE-UA优化算法是一种全局优化算法，该方法被认为能够较好的解决水文模型参数优选过程中的5个主要特征[20]，王海元等[21]将SCE-UA算法应用在暴雨强度公式参数优化中，并与其它算法的优化结果进行比较，发现SCE-UA算法能够有效地处理高维参数优化问题。

4 实例分析

4.1 暴雨样本系列选样

自贡气象观测台于1955年1月1日建站，现位于流井区彩灯公园内，经度104°46′E、纬度29°21′N，海拔高度为352.6 m。自贡气象站是国家基本站，从1956年开始观测降雨量，其雨量测量、记录工具等均符合国家规范。

自贡气象站有1963—2015年共53 a的年最大暴雨资料。采用年最大值法在自贡气象站N年降雨资料中选取N组历年各历时的暴雨最大值。采用的降雨历时取10，20，30，60，90，120，150，180，360，1 440 min共10个历时；计算降雨重现期按2，5，10，50，100 a共5个重现期。图1为自贡气象站1963—2015年年最大暴雨量时序曲线。

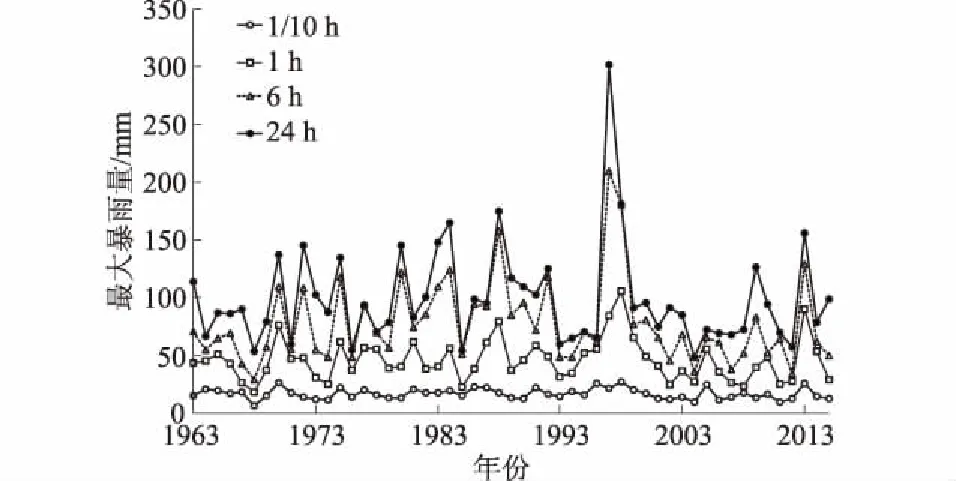
图1 自贡气象站1963—2015年年最大暴雨量时序曲线Fig.1 Time sequence of maximum storm at Zigong meteorological station from 1963 to 2015

4.2 暴雨频率分布参数估计

根据自贡气象站1963—2015年共53 a的各历时年最大暴雨样本系列，进行年最大暴雨频率计算。采用数学期望公式和钱穆公式计算经验频率，由矩法初估参数，以P-Ш型频率曲线拟合点据，取偏态系数Cs与变差系数Cv的比值Cs/Cv=3.5，目估适线分析确定统计参数和设计值，其计算结果见表1。图2为自贡气象站历时360 min和1 440 min下的暴雨频率曲线。

4.3 暴雨强度公式参数求解

根据表1计算自贡气象站不同频率下各历时的平均暴雨强度，见表2。

4.3.1 水利行业暴雨强度公式计算结果

水利行业在采用暴雨强度公式计算暴雨设计值时，一般在双对数坐标系中采用分段直线拟合法。由于公式中仅含有2个参数，根据双对数坐标系中区间直线两端的暴雨历时和平均暴雨强度即可确定

表1 自贡气象站不同历时下设计暴雨成果Table 1 Calculation results of rainstorm frequency withdifferent durations at Zigong meteorological station

图2 自贡气象站历时360 min和1 440 min下的暴雨频率曲线Fig.2 Curves of rainstorm frequency lasting 360 min and 1 440 min at Zigong meteorological station

表2 自贡气象站暴雨强度-历时-频率IDF关系Table 2 Intensity-diachronic-frequency (IDF) relation ofrainstorm at Zigong meteorological station

公式中2个参数。采用水利行业的暴雨强度公式，历时取10,60,360,1 440 min 4种情况，并计算历时20，30，90，120，150，180 min 6种情况的平均暴雨强度，计算结果见表3。

表3 自贡气象站不同历时下平均暴雨强度计算成果Table 3 Calculation results of average rainstorm intensitywith different durations

4.3.2 市政行业暴雨强度公式计算结果

采用第3节建立的暴雨强度公式参数优化求解方法，对市政行业暴雨强度公式进行参数求解，并计算平均绝对均方根误差，均方根误差越小，拟合效果越好，计算结果见表4。

表4 市政行业暴雨公式计算的自贡气象站参数成果表Table 4 Parameters calculated by rainstorm intensityformula of municipal industry

由表4可知，采用市政行业暴雨强度公式计算的理论曲线与实测值的平均绝对均方根误差为0.01～0.03 mm/min，符合《室外排水设计规范》(GB 50014—2006)中该指标≤0.05 mm/min的要求。表明本文构建的一种新的对数离差绝对值和最小准则(简称“LWAS准则”)作为优化目标函数，不仅可以兼顾到IDF曲线的下端拟合情况(指历时较大的情况)，而且可以满足平均绝对均方根误差不大于5%的要求。这说明，将SCE-UA算法应用于暴雨强度公式的参数优化求解是可行的，并且能够取得较好拟合效果。

根据表4中自贡气象站暴雨强度公式参数成果，在双对数坐标系中绘制暴雨强度公式计算的暴雨强度-历时-频率关系曲线(IDF曲线)，以暴雨历时D为横坐标的对数曲线，以平均暴雨强度I为纵坐标，按照频率P绘制，计算成果见图3。由图3可知，IDF曲线的形状为向下弯曲的，符合各地区暴雨强度随暴雨历时的变化规律；暴雨衰减指数n值随着暴雨历时的变化而发生明显的转折，在10 min和100 min附近的IDF曲线转折程度最大。

图3 自贡气象站暴雨强度-历时-频率IDF曲线Fig.3 Curves of intensity-diachronic-frequency (IDF) relation of rainstorm at Zigong meteorological station

4.4 结果对比分析

将水利行业与市政行业暴雨强度公式计算的各历时20，30 ，90 ，120，150，180 min平均暴雨强度与实测值相减，计算结果见图4。由图4可知，当P=1%时，水利行业暴雨强度公式与实测值的平均绝对误差为-0.34 mm/min，市政行业暴雨强度公式与实测值的平均绝对误差为0.03 mm/min；当P=10%时，水利行业暴雨强度公式与实测值的平均绝对误差为-0.19 mm/min，市政行业暴雨强度公式与实测值的平均绝对误差为0.05 mm/min。可见水利行业暴雨强度公式计算各历时的暴雨强度值普遍偏小，市政行业暴雨强度公式可以较好地拟合各历时的暴雨强度实测值。

图4 水利行业和市政行业暴雨强度公式计算值与实测值绝对误差Fig.4 Absolute errors of results calculated by rainstorm intensity formulae of water conservancy industry and municipal industry

当P=1%时，在双对数坐标系和双线性坐标系中分别绘制水利行业和市政行业的暴雨强度公式计算的IDF曲线，计算结果见图5。由图5(a)可以知道，在双对数坐标系中，水利行业IDF曲线在市政行业IDF曲线的下方，其平均暴雨强度均偏小。随着历时的减小，两者误差增大，尤其在历时为30 min左右，两者相差最大。这说明，水利行业采用的分段暴雨强度公式在拟合实测暴雨强度值时存在较大的偏差。由图5(b)可知，在双线性坐标系中，同一设计频率P下，平均暴雨强度和暴雨历时呈现高度的非线性相关关系。当P=10%时，在双对数坐标系和双线性坐标系中，各行业IDF曲线分别位于P=1%时的IDF曲线的下方。不同频率下的IDF曲线之间的差距随着历时D的变化呈现非线性变化规律。

图5 水利行业和市政行业暴雨强度公式计算的IDF曲线对比示意图Fig.5 Comparison of intensity-diachronic-frequency(IDF) curves obtained by rainstorm intensity formulae of water conservancy industry and municipal industry

5 结 论

通过对比分析我国水利行业和市政行业暴雨强度公式计算过程，建立了基于SCE-UA优化算法的暴雨强度公式参数求解方法，并以自贡气象站暴雨强度公式拟合为例进行了对比分析，得出以下结论：

(1)SCE-UA算法能够有效地解决复杂的暴雨强度公式参数求解难的问题，能够快速、高效地收敛到全局最优解。

(2)同一设计频率下，平均暴雨强度和暴雨历时呈现高度的非线性关系；水利行业暴雨强度公式在计算各历时暴雨强度时普遍偏小，存在较大的偏差；市政行业暴雨强度公式可以较好地拟合各历时的暴雨强度实测值。