基于联系数的水闸安全综合评价物元模型与实现方法

，

(河海大学 a.水文水资源与水利工程科学国家重点实验室； b.水利水电学院，南京 210098)

1 研究背景

水闸是水利工程中重要的基础建筑物[1]，具有挡水、泄水双重作用，在平原地区应用广泛。据文献资料统计，我国现有水闸多修建于20世纪50—70年代，受当时经济、技术等诸多因素的限制，绝大多数水闸的设计与施工不够合理，致使现存水闸普遍存在防洪标准偏低、结构稳定性差、结构损伤、渗流破坏、金属结构机电设施老化等病险问题[2-3]。为保障水闸工程安全，及时进行除险加固，需要在对安全性、适用性、耐久性等指标进行单一分析的基础上，合理、科学地开展水闸工程的综合评价。

水闸工程结构复杂，其安全指标的影响因素众多，因而水闸的安全综合评价是一项复杂的系统工程[4]。目前一些学者基于层次分析法、灰色综合评价法、模糊综合评价法和物元分析法等[5-7]，结合水闸工程专业知识，从指标体系构建、指标度量方法、指标权重确定、综合评价数学模型等方面对水闸工程安全综合评价开展研究。但由于影响水闸综合性能的因素较多，并且具有模糊性、随机性、不完整性等特征，造成已有的成果多存在主观性强、人为参与多、对水闸工程运行状态及发展趋势的预估能力不足等问题。

为了减少主观随意性的影响，提高评价方法的精度，本文将联系数原理引入物元理论，构建基于联系数的物元模型，对水闸安全评价中的不确定性因素进行刻画，将确定性分析与不确定性分析相结合，以期实现对水闸工程运行状态及发展趋势的综合评价。

2 水闸安全综合评价指标体系

基于水闸构筑物各性态指标的监测资料，对其进行安全综合评价。根据相关规范标准及文献资料[8-12]，水闸工程安全评价的指标体系可分为3个层次：第1层为评估的目标层，即水闸工程安全状态；第2层为评估的准则层，分别为安全性、适用性与耐久性；第3层为影响因素层。由此构建的水闸工程安全评价指标体系如图1所示。

3 基于四元联系数的水闸安全综合评价物元模型

3.1 物元模型

物元模型是一种能够对事物特征进行数学描述的模型，是处理确定与不确定性问题的基本模型[13-16]。物元通常由事物(M)，事物的特征(C)及对应的量值(V)构成的有序三元组来表示，用符号R=(M,C,V)表示，也称为事物的基本元。

由于水闸工程安全综合评价涉及多个评价指标，作为一个具有多特征的事物，其物元模型用矩阵可表示为

(1)

式中：M表示水闸安全综合评价；C表示评价指标；V表示评价指标的量值；n表示评价指标的数量。

3.2 四元联系数

集对分析是由赵克勤[17]于1989年提出的一种处理随机、模糊以及不确定性问题的系统分析方法，并使用“联系数”来描述对应集合之间的所具有的同、异、反的特征。分别引入同一度、差异度、对立度3个概念定量描述评价指标集与目标集之间的确定与不确定性关系。其同异反联系数的基本表达式为

u=a′+b′i′+c′j′ 。

(2)

式中：a′,b′,c′均在[0,1]取值，分别表示集对同一特性数目、差异特性数目和对立特性数目所占总数的比例，即a′为同一度、b′为差异度、c′为对立度，显然，a′+b′+c′=1；u为同异反联系数；i′为差异度标记符号或差异度系数，取值区间为[-1,1]，根据具体情况取值；j′为对立度标记符号或对立度系数，一般取值为-1，此外，i′，j′也可不取值，作为标记符号。

四元联系数[18-19]是根据同异反联系数在b′i′项上展开得到，其表达式为

u=a+bi+cj+dk。

(3)

式中：a,b,c,d均在[0,1]取值，a为同一度，b为偏同差异度，c为偏反差异度，d为对立度，且a+b+c+d=1；i，j为差异不确定系数，i∈[0,1]，j∈[-1,0]；k为对立系数，k=-1；i，j，k也可不取值，作为标记符号。

在实际应用中，可将联系数与安全评价的级别对应起来[20-21]。水闸工程根据安全类别可划分为一类、二类、三类、四类水闸，分别对应正常、基本正常、轻度异常、危险4个等级，据此本文采用四元联系数进行水闸安全评价：用a刻画“一类水闸”，b刻画“二类水闸”，c刻画“三类水闸”，d刻画“四类水闸”，即a，b，c，d分别表征某一评价指标隶属于各级水闸的测度，i，j，k作为标记符号，不予取值。

3.3 联系势原理

当n元联系数u=a+b1i1+b2i2+…+bn-2in-2+cj中c≠0时，定义同一度a与对立度c的比值a/c为该联系数在指定问题背景下的联系势S[17]，即S=a/c。

利用联系势的概念[22-23]可以把水闸运行状态的发展趋势分为同势、均势和反势3类。当S>1时，表示水闸运行状态的发展趋势处于同势，即目前的运行状态向危险等级恶化的风险很小，具备向更安全等级发展的潜力；当S=1时，表示水闸运行状态的发展趋势处于均势，即为一种既不表现出恶化又不表现出好转的临界状态，此时外界影响因素稍加改变，均势状态就会打破；当S<1时，表示水闸运行状态的发展趋势处于反势，即目前的运行状态向危险等级恶化的风险很大。

3.4 基于联系数的水闸安全综合评价物元模型

本文将四元联系数引入水闸安全评价的物元模型，即安全评价指标的量值以四元联系数的形式表达，从而构造出基于四元联系数的水闸安全综合评价物元模型。其表达式为

(4)

式中u为单指标联系数。

对于归一化后介于[0,1]区间的效益型评价指标C，其单指标联系数u可按以下准则计算：若评价指标值x位于某等级对应的评价区间上，则与该等级对应的联系数取1；相邻等级的联系数在[0,1]区间以线性插值的形式获得；其余等级的联系数均取为0。

对上述准则所得的四元联系数作归一化处理，得到计算公式为

(5)

式中：x为评价指标值；v1,v2,v3均为划分水闸各安全评价等级的阈值。

将计算所得的各个单指标联系数u1,u2，...，un代入式(4)即构建出四元联系数的水闸安全综合评价物元模型。

4 水闸安全综合评价实现过程

4.1 安全综合评价指标与分级

根据构建的水闸安全评价指标体系，以安全性、适用性、耐久性为评价指标建立评价模型，根据水闸安全类别可划分为一、二、三、四类水闸，分别对应正常、基本正常、轻度异常、危险4个等级，其中，鉴定结果为三类或四类水闸均属于病险水闸。具体分级标准如表1所示。

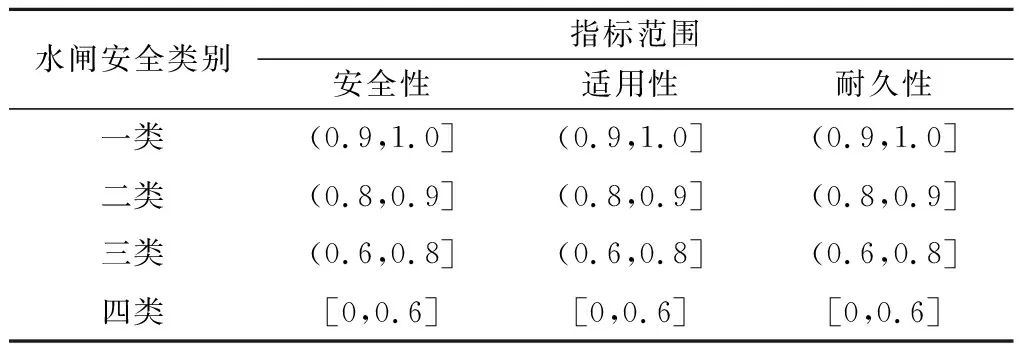
表1 水闸安全评价指标分级Table 1 Grading on evaluation indexes of sluice project

4.2 计算步骤

第一步，依据选定的评价指标及式(4)构建基于四元联系数的水闸工程安全综合评价物元模型，即

第二步，利用式(5)计算各指标的四元联系数u1,u2,u3，并通过专家打分法确定指标权重w1,w2,w3。

第三步，计算最终的合成联系数u，即

(6)

第四步，通过得到的合成联系数对水闸安全状况进行评价，鉴定水闸等级，并依据联系势原理对其运行状态的发展趋势进行评估。

5 实例分析

某枢纽工程为Ⅱ等大(2)型工程，节制闸、进洪闸、闸室等主要构筑物等级为2级，次要构筑物等级为3级。为了深入了解水闸目前的运行状态，以开展除险加固工作，依据相关监测数据与现场考察情况，对该水闸工程进行安全综合评价。

5.1 基础数据

通过专家打分,经归一化处理后得到的安全性、适用性、耐久性的评分值分别为0.839 2，0.758 4，0.692 9。

5.2 基于四元联系数的物元模型与权重矩阵

根据前述原理，按照式(5)分别计算各指标的等级联系数，构造基于四元联系数的水闸安全评价物元模型为

R=

依据专家打分及层次分析方法，得到指标权重矩阵W=[w1,w2,w3]=[0.541,0.201,0.258]。

5.3 合成联系数

依据式(6)计算合成联系数，其计算式为

0.106+0.410i+0.394j+0.090k。

5.4 成果分析

根据计算所得的合成联系数u=0.106+0.410i+0.394j+0.090k，可知，i项系数最大，故该水闸的安全鉴定结果为二类水闸，说明该水闸构筑物符合安全运行标准，这与文献[4]的结论一致。

由于合成联系数中与病险状态直接相关的j项系数大小仅次于i项系数，且差距较小，故有必要考察该水闸未来运行状况的发展趋势。根据联系势原理，计算合成联系数的联系势S=0.106/0.090=1.18，其值>1，故水闸运行状态的发展趋势处于同势，即该水闸工程目前的安全状态向病险状态(三类水闸)发展的风险较小，但考虑到1.18很接近1，表明该水闸的运行状态基本处于正常运行状态的极限，一旦相关影响因素稍加改变就很有可能向病险状态发展。

上述分析表明，该水闸工程目前运行情况安全，鉴定结果为二类水闸，暂时不需要开展除险加固工作，但考虑到其运行状态接近正常运行的极限状态，应当加强日常的监测与巡查，关注其后续安全状态的发展趋势。

6 结 语

水闸工程的安全评价是一个涉及多层次、多指标的复杂系统工程。本文将四元联系数原理与物元理论结合，构建了基于联系数的水闸安全综合评价物元模型，从同、异、反3个方面对评价过程中存在的不确定性问题进行了分析。

(1)基于联系数的物元模型将确定性分析与不确定性分析相结合，较好地解决了水闸安全评价中指标间存在的不相容性与关联性问题，并能基于联系势原理对水闸运行状态的发展趋向进行评估。

(2)相较于传统物元分析方法，基于联系数的物元模型计算方法更为简单。计算实例表明，该评价方法对于某水闸的鉴定结果与文献[4]以及河海大学水工结构研究中心的鉴定结果一致，由此证明，将基于联系数的物元模型应用于水闸安全综合评价是可行的，这也为其他水工建筑物的安全评估提供了新思路。

(3)本文在单指标联系数的计算过程中选用了简单的线性插值方法，至于是否存在更加合理有效的数值计算方法，尚有待进一步探究。