卫星导航定位误差仿真分析

, ,,

(1.上海机电工程研究所,上海 201109; 2.上海无线电设备研究所,上海 200090)

0 引言

卫星导航系统是利用卫星进行自动地理位置定位的系统，允许小型电子接收机通过接收卫星发射的无线电信号确定自身位置。全球导航卫星系统(global navigation satellite system，GNSS)是具备全球覆盖能力的卫星导航系统。目前，只有美国的GPS和俄国的GLONASS是属于运行中的全球导航卫星系统；我国的北斗卫星导航系统预计到2020年达到全球覆盖的能力；欧盟的Galileo导航系统仍然处于初步部署状态，最早也要到2020年才能运行[1]。

美国的GPS全球定位系统耗时20年，到1994年全部建成并投入使用。该系统由20 180 km轨道上的21颗工作卫星和3颗备份卫星组成，均匀分布在六个倾角为55°的轨道平面上，周期为11小时58分钟，可以为用户提供全球性、全天候、连续实时和高精度的三维位置、速度和时间信息，是迄今为止全球技术最成熟、应用最广泛的卫星导航系统[1-3]。该定位系统具体由三部分构成：空间星座部分、地面控制部分和用户设备部分。空间星座部分就是24颗卫星，采用码分多址(CDMA)区分，每颗卫星以相同的频率和调制方式采用各自唯一的伪随机码发射信号。地面控制部分则是一个主控制站，5个全球监测站和3个地面控制站组成。用户设备部分就是全球任意位置的各种GPS接收机、数据处理软件等，其作用是通过接收GPS卫星信号，提取观测到的卫星信息和参数，经过数据处理，实现定位和导航[4]。

卫星导航定位技术已应用于多个领域，尤其在测绘、勘探、车辆定位、军工等方面[5]。定位精度是卫星导航最为重要的指标之一，是指测量点位误差分布的离散于密集程度，是测量点位于真是点为之差的概率统计几何平均值[6]。本文从卫星导航的测量原理出发，按照单点定位方法，对真实运动状态进行定位误差进行仿真研究。

1 卫星导航测量原理

GPS卫星导航定位设备通过接收多颗卫星发布的信号，结合星历表信息，测量和解算出每颗卫星发射信号时的位置参数和GPS系统的时间参数。卫星导航定位设备内装有与GPS系统时间同步的精密时钟，可用于测量卫星信号在空间的传播时间，计算卫星到定位设备的距离。如果已知GPS卫星导航定位设备与三颗卫星的距离时，就可以实现定位设备的三维导航定位[7]。即：分别以三颗卫星为中心，以所知的三颗卫星的距离为半径，绘制三个球面，卫星导航定位设备就位于球面的交点。

距离计算是全球导航定位测量的关键，主要从接收信号中提取。导航定位设备接收到的不同的卫星发射出的信号，其延时和附加的多普勒频移是不同的。位于用户接收机正上方的卫星没有多普勒频移，其最近距离为20 183 km，位于地平线方向上的卫星就有最大的多普勒频移，其最大值可达±5 kHz，最大距离为25 783 km。一个典型的GNSS信号结构如图1所示。

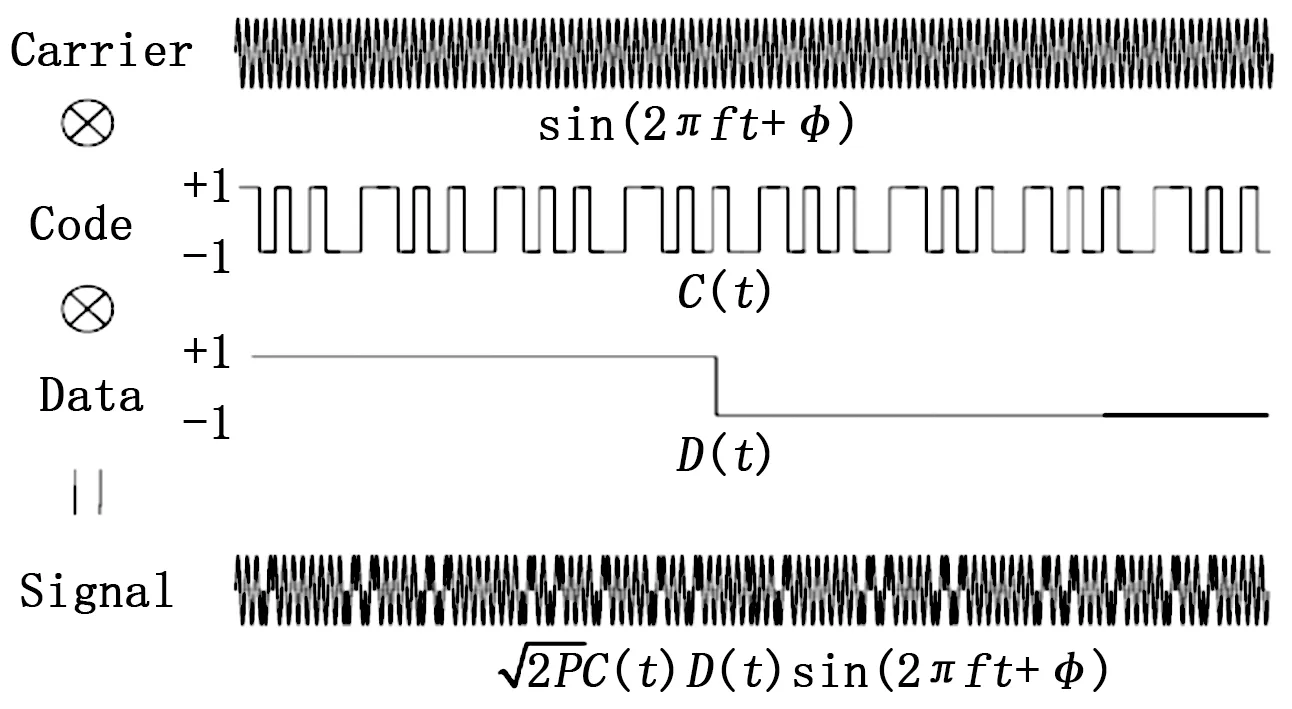
图1 GNSS信号结构

GNSS信号通常是由载波、伪随机码和导航数据信息相乘而得到。对于几种不同的卫星导航系统，其具体的参数有所不同，比如载波频率、编码方式等[8-9]。

上述公式还可以进一步详细表达为：

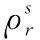
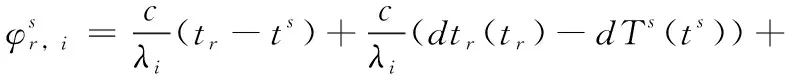
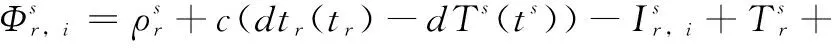
式中，

对流层模型和电离层模型对伪距测量具有重要作用。标准大气可表示为：

p=1013.25×(1-2.2557×10-5h)5.2568

T=15.0-6.5×10-3h+273.15

其中:z为天顶角(rad)。

通过使用广播的电离层参数pion=(α0,α1,α2,α3,β0,β1,β2,β3)，并利用如下各式可推导出电离层延迟模型，也叫Klobuchar模型：

ψ=0.0137/(El+0.11)-0.022

φi=φ+ψcosAz

λi=λ+ψsinAz/cosφi

φm=φi+0.064cos(λi-1.617)

t=4.32×104λi+ti

F=1.0+16.0×(0.53-El)3,

2 定位方法

本文仿真是采用最小二乘估计方法来进行单点定位计算。假设给定一个测量矢量y，并可以用未知参数矢量x和随机测量误差v的线性方程表示：

y=Hx+v(2-28)

最小平方代价函数JLS定义为均方误差之和：

则可以进一步表示为：

JLS=(y-Hx)T(y-Hx)

为了最小化代价函数，可以另其梯度为零，则：

如果测量不满足线性关系，而是非线性函数关系：

y=h(x)+v(2-33)

其中:h(x)是未知参数矢量x的函数，利用泰勒级数展开：

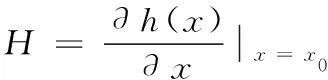
忽略二阶以上泰勒展开项，可近似为：

y≈h(x0)+H(x-x0)+v

上述计算要求初始参数x0比较接近真实值；但如果初始参数并不接近真实值，则可以通过迭代方法改进：

如果迭代收敛，最终将得到估计的参数：

上述迭代最小二乘法又通常称为高斯-牛顿法。值得注意的是简单的高斯-牛顿方法其迭代并不总是收敛，尤其是具有较大非线性度的测量方程。针对这种情况可以采用最为流行的LM(Levenberg-Marquardt)法。

3 卫星定位误差源分析

从卫星定位方法可得出，导致卫星导航系统的定位准确度产生误差的因素有：

卫星自身、信号传播路径、用户接收设备三个部分[10]。卫星部分包括卫星星历误差、卫星钟差和卫星屏蔽角；信号传播误差：大气电离层以及对流层的存在，从而对卫星传输信号造成的时延、卫星传输信抵达地球表面后，由于存在多路径传播导致的信号干涉等；由于接收方的信号接收设备问题导致的测量误差，以及由于相对论效应导致的接收设备的时钟误差。

3.1 卫星部分误差

卫星自身导致的误差因素有卫星星历误差、卫星时钟差和卫星屏蔽角三种。

卫星的星历误差即卫星实际所在的位置与星历中的位置不一致而导致的误差。该误差包含两个部分：其一，星座自主导航确定的卫星位置误差；其二，坐标转换过程中的地球定向参数误差。

卫星的时钟误差会对作用于导航系统于轨道内的自身导航以及传输于用户的卫星星历，严重影响最终的导航精度。

测距误差即为导航系统的时间与卫星时钟之间的差值与光速的乘积。为减小误差，在进行系统导航前，对之前数个时段的钟差数据进行拟合，获取时钟差参数。在导航进行过程中，该系统参数发送给用户，并用于较准。

在定位过程中，可观测到的卫星数量越多，定位精度计算中，可应用的信息越多，导航定位也越准确。为方便表述，将“可观测到的卫星数量多少的量”，用卫星屏蔽角来表示。即卫星屏蔽角越大，可观测到的卫星数量越多。

3.2 信号传播误差

信号传播误差是指卫星发向地面接收设备的信号在传输途中中受到介质、折射、多径等影响导致信号传输延迟产生的偏差。信号传播延迟包括电离层、对流层延迟以及多路径延迟。

电离层距离地面50～1 000 km，电离层内存在大量自由电子和带电离子，从而导致卫星信号传输速度及路径发生微小偏离，最终影响定位精度。

对流层距离地表低于50 km，对流层中的大气温度、压力、湿度会对传输信号的高频部分的传输带来时延，对其传输速率会造成一定的影响。

多路径效应影响是由于卫星信号到达地面后存在多路径传播导致信号干涉现象，产生定位结果偏差。导航系统工作时，卫星导航定位设备接收到附近物体反射的卫星信号，将与天线直接收到的卫星信号形成叠加和干涉，导致多路径误差的产生。

3.3 用户接收设备引入偏差

用户接收设备引入偏差主要指接收机在测量过程中引入的定位偏差。它主要包括因接收设备的设计和生产过程中带来的测量误差，以及相对论效应引入的接收设备时钟误差。

用户接收设备定位误差可分为系统定位误差和随机定位误差。系统定位误差主要指卫星导航测试设备在设计、调试和使用过程中，在满足指标的前提下，定位结果存在一个固定的偏差。系统定位误差可以通过更好的仪器设备、多次测试等手段，减小系统定位误差。随机定位误差主要指卫星导航接收设备不可避免的受到内部的电子元器件产生的热噪声和散弹噪声的影响，且这些噪声随设备开启加电时间越长，温度越高，噪声越大，这些随机误差将直接导致卫星导航定位偏差。

相对论效应是指在不同的运动速度、加速度条件下，在卫星的时钟和接收设备的时钟之间产生相对时钟差的现象，再乘以光速就是实际产生的测量误差。

4 运动轨迹建模

依据上述误差分析，卫星导航定位与卫星、信号传播、接收设备三个方面的多个细节相关。在运动轨迹建模过程中，考虑所有的因素将使问题过分复杂化。因此，本误差分析仿真主要着重考虑卫星屏蔽角、电离层延迟、对流层延迟以及多路径延迟的变化，对汽车、飞机、轮船的运动轨迹，在位移误差、速度误差方面进行建模和仿真。

采用Matlab软件，根据卫星导航测量原理和定位方法，对一条真实的汽车运动轨迹进行建模，并以这条轨迹作为参考来研究卫星导航定位误差的结果。

假定初始位置误差rebn=[4,2,3](北、东、地，单位m)，初始速度误差vebn=[0.05,-0.05,0.1](北、东、地，单位m/s)。

真实的载体运动轨迹如图2、3所示。该轨迹模拟的是汽车60 s时间内的位移、速度的运动情况。

图3 真实载体速度

5 位移误差仿真分析

5.1 影响参数敏感度仿真

为探索位移误差变化规律，并验证定位误差仿真模型有效性。对卫星屏蔽角、电离层误差、对流层误差、多路径效应进行独立依次变化，进行仿真、验证和计算。

设定初始条件：假设初始估计位置rinit=[0,0,0]m(ECEF)，接收周期T=1 s，卫星屏蔽角θmask=10，电离层误差riono=2 m，对流层误差rtrop=0.2 m，多径效应误差rtrack=1 m，初始接收时钟偏差rclock=10 000 m，初始接收时钟漂移vclock=100 m/s。

仿真结果如4所示。从图4位移误差变化可以看出，北向位移和东向位移误差均在2 m范围内波动；地向位移误差则在5 m范围内波动。

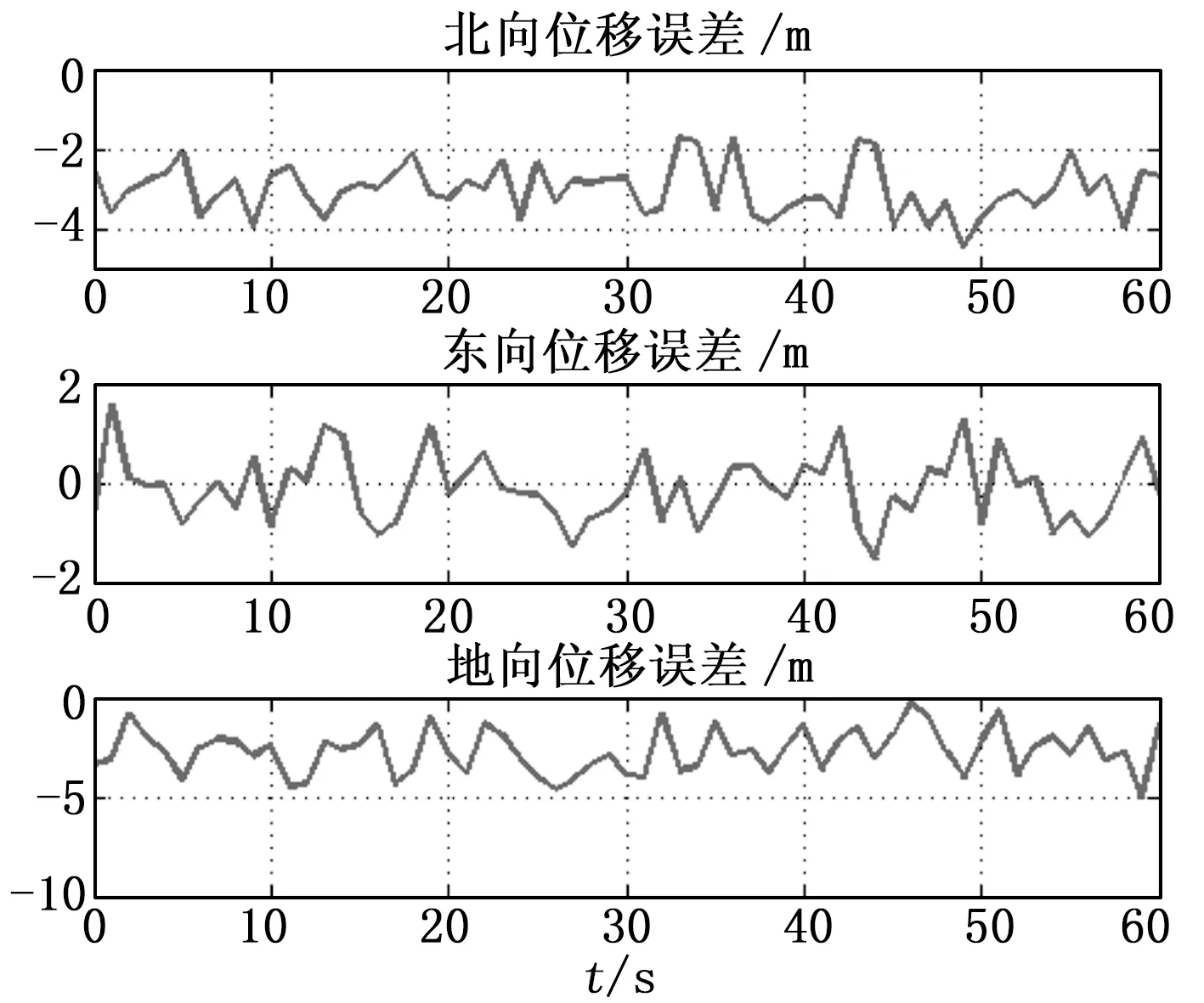
图4 卫星屏蔽角10度位移误差

卫星屏蔽角从10变化到20，即θmask=20时，仿真结果如图5所示。与初始状态相比较，只增大了卫星屏蔽角(意味着观测到的卫星数量减少)，各个方向的位移误差明显增大，约为前者的2倍。因此，这说明了观测到的卫星数量对导航误差影响较大。

图5 卫星导航位移误差#2

同样的方法分别对电离层延迟、对流层延迟和多径效应进行仿真，结果如下。

与初始条件相比较，仅电离层延迟引起的误差增大到原来2倍，其它条件不变。仿真结果表明，位移误差产生了一个固定的偏移，但波动幅值变化很小；

与初始条件相比较，仅对流层延迟引起的误差增大到原来2倍，其它条件不变。仿真结果表明，位移误差产生了一个固定的偏移，但波动幅值变化很小；

与初始条件相比较，仅多径效应引起的误差增大到原来2倍，其它条件不变。仿真结果表明，多径效应误差增大后，各向位移误差波动均增大。

5.2 不同载体运动的位置误差分析

在汽车运动状态下，可观测到的卫星数量、电离层和对流层延迟以及多径效应引起的误差对卫星导航精度存在影响。其他载体运动时，在这些因素下，是否会有其他的变化。为此，对飞机和轮船进行仿真对比。

5.2.1 飞机运动仿真

设定飞机运动初始条件：运动总时间为418 s，且初始条件为初始估计位置rinit=[0,0,0]m(ECEF)，接收周期T=1 s，卫星屏蔽角θmask=10，电离层误差riono=2 m，对流层误差rtrop=0.2 m，多径效应误差rtrack=1 m，初始接收时钟偏差rclock=10 000 m，初始接收时钟漂移vclock=100 m/s。

模拟的飞机运动如图6所示。

图6 飞机参考运动位移

仿真得到的卫星导航位移误差变化如图7所示。

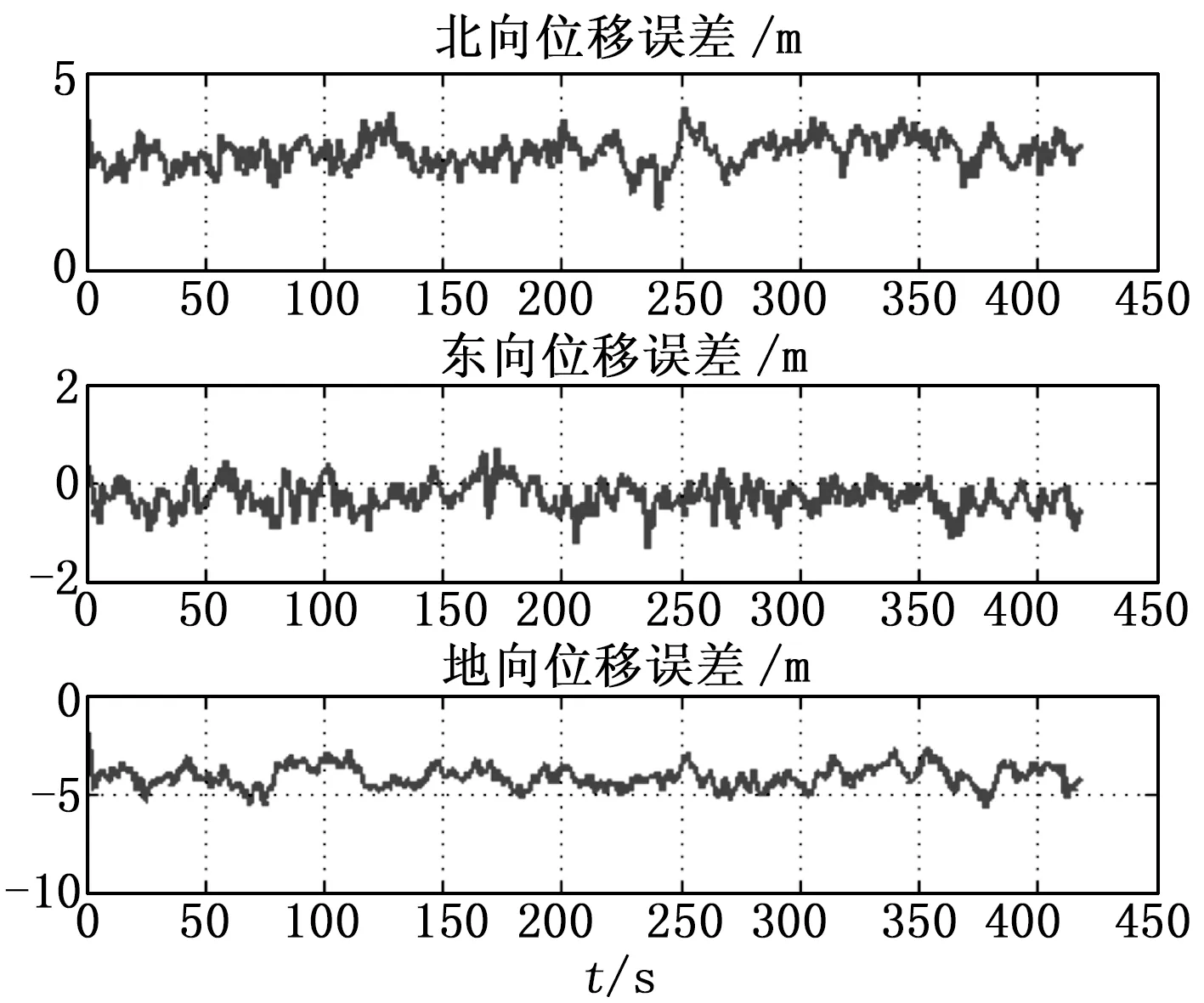
图7 卫星导航位移误差(飞机)

5.2.2 轮船运动仿真

设定轮船运动初始条件：运动总时间为300 s，且初始条件为初始估计位置rinit=[0,0,0]m(ECEF)，接收周期T=1 s，卫星屏蔽角θmask=10，电离层误差riono=2 m，对流层误差rtrop=0.2 m，多径效应误差rtrack=1 m，初始接收时钟偏差rclock=10 000 m，初始接收时钟漂移vclock=100 m/s。

模拟的舰船运动轨迹如8所示。

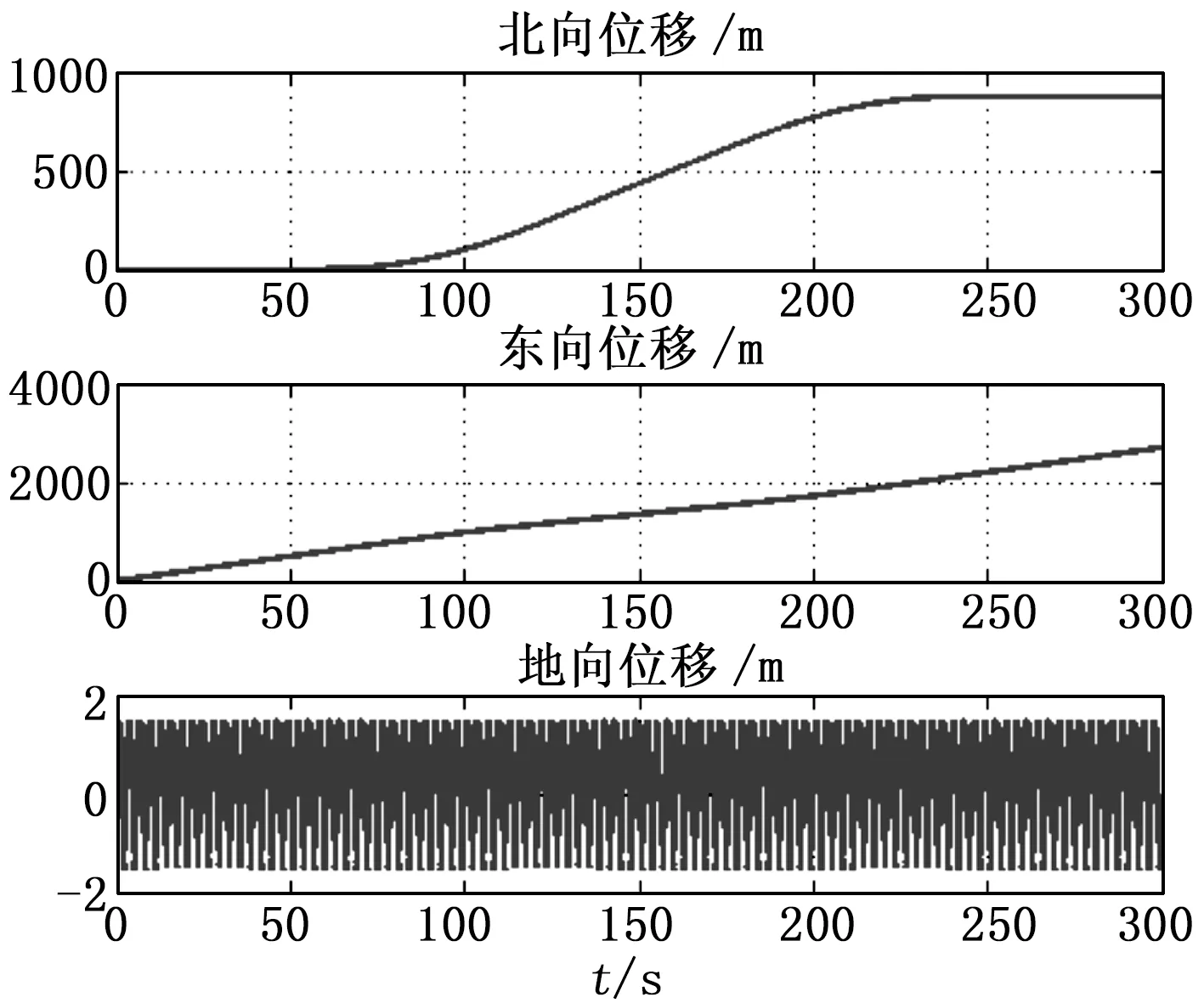
图8 轮船参考运动位移

仿真得到的卫星导航位移误差，如图9所示。

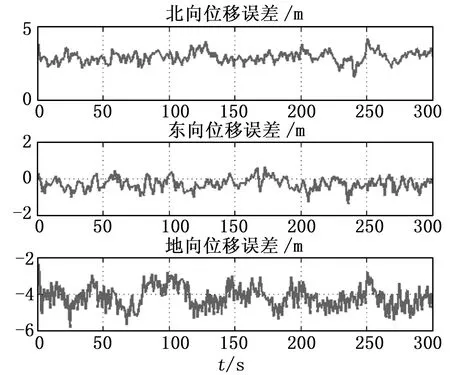
图9 卫星导航位移误差(轮船)

从汽车、飞机、轮船三种常见载体的运动仿真判断，说明了载体的运动方式对卫星导航定位位置计算的影响很小。

6 速度误差仿真分析

同样方法，分别对汽车、飞机、轮船的的速度建立Matlab仿真模型，进行仿真分析，有以下结论：

1)初始状态的速度误差变化情况，北向速度和东向速度误差均在0.05 m/s内波动；地向速度误差偏大，在0.1 m/s范围内波动。

2)与初始条件相比较，只增大了卫星屏蔽角(意味着观测到的卫星数量减少)，速度误差也明显增大，除了东向速度误差变化不大外，北向和地向速度误差均增大约2倍。因此，这说明了观测到的卫星数量对导航误差影响较大。

3)与初始条件相比较，只是对流层延迟引起的误差增大到原来2倍，其它条件不变。仿真结果表明，对流层误差变化并不影响速度误差的变化。这说明电离层和对流层对卫星导航的影响规律相似。

4)与初始条件相比较，只是多径效应引起的误差增大到原来2倍，其它条件不变。仿真结果表明，多径效应误差变化仍然并不影响速度误差的变化。

5)对汽车、飞机和轮船为载体运动的速度误差进行仿真分析，仿真结果表明，速度误差和位移误差的变化相似，即载体的运动方式对卫星导航定位算法的影响很小。

7 结束语

针对卫星导航的误差分析问题，进行了大量的仿真试验，试验结果均表明，对于卫星导航而言，不同载体的运动对导航误差的影响很小，同时其误差特性是在一定范围内波动，不会随时间累积而增加。对卫星导航的精度影响较大的是可观测到的卫星数量、电离层和对流层延迟以及多径效应。