基于积温效应和优化支持向量机的短期电力负荷预测
谭风雷,陈梦涛,汪龙龙
(国网江苏省电力有限公司 检修分公司,南京 211102)
电力负荷预测是电力系统规划、运行和调度的基础和关键。电力负荷预测根据预测时间的长度,一般可分为短期负荷预测、中长期负荷预测[1—3]。实际上,影响电力负荷预测精度的因素十分复杂,需要考虑到各个方面的因素,例如是否是节假日、气象状况、经济条件、社会问题和政治因素等。只有充分考虑各个方面的因素,才能有效提高负荷预测精度[4—6]。但是实际上,有很多因素具有不确定性、随机性,给负荷预测带来了难度。而气象状况[7—8]作为可预知的因素,对整体负荷影响较大,具有较高的研究价值和研究意义。因此,本文将重点研究气象状况对负荷的影响。
文献[9]采用了支持向量机预测负荷,对参数选取进行了分析,但是没有给出具体算法。文献[10]—文献[12]分别采用遗传算法粒子群和模拟退火法优化支持向量机来预测负荷,得到了较好的预测效果,但是缺优化算法的比较分析。本文提出了一种考虑温度积累效应的负荷预测方法。首先研究积温效应的2种表现形式和特点;在此基础上建立考虑积温效应的温度修正模型;最后借助江苏某地区历史数据作为研究对象,采用最小二乘法优化积温效应相关参数,对负荷值进行预测,预测结果验证了该方法的有效性和正确性。
1 积温效应
随着电力负荷对气象因素敏感程度的增加,气象因素对负荷的影响也越来越大,积温效应作为一种反应负荷变化的气象因素,在负荷预测中占据了较高的比重,因此负荷预测时考虑积温效应是十分有意义的,可以有效提高预测精度[6—7]。
1.1 积温效应分析及量化
目前,电力系统中负荷的积温效应通常意义上讲是指在长时间低温或高温气象状况下,负荷会出现不同程度的反常变化。但实际上当2天之间温度差大于一定值时,根据负荷的连续性和惯性原理,使得负荷相差较小,这样就会使相同温度在不同时间段,对应的负荷相差较大,这一点是目前负荷预测中往往没有考虑到的地方,具有较高的研究价值[7]。结合积温效应的表现形式和特点,文中将前者称为多日积温效应,后者称为2日积温效应。综合考虑积温效应的2种表现形式,提出了一种考虑温度积累效应的温度修正方法
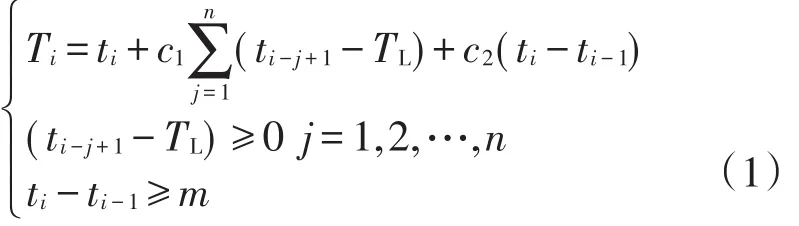
式中:Ti,ti分别为第i个预测日的修正温度值和实际温度值;c1,c2分别为考虑多日积温效应和2日积温效应的修正系数;n为积温效应持续天数;TL为温度下限;m为相邻2天的温差,修正温度预测负荷之前需要确定n、TL和m。
1.2 积温效应参数确定
目前,针对积温效应参数n和TL很少有文献给出明确的确定方法,都是通过某地区的历史数据大致确定一个范围,在此背景下,本文提出一种具体有效的积温效应参数确定方法。
积温效应参数确定方法的具体步骤:
(1)分别研究日最高温度、日平均温度、日峰负荷所对应温度与日峰负荷的相关性,选择与其相关性最大的温度作为本文温度的研究对象;
(2)建立步骤(1)所得到的温度与日峰负荷的线性回归模型,剔除误差较大的点(本文设定为4%)所对应的温度和负荷数据,这些剔除的负荷数据可能是有积温效应的负荷

式中:Pi(ti)为第i个预测日的预测负荷;ti为第i个预测日的实际温度;a、b分别为回归方程的系数;
(3)将剩下的温度和负荷作为研究的对象,重新执行步骤(2),直到所有的负荷数据的误差都小于4%;
(4)将所有剔除点所对应的温度和负荷数据作为积温效应数据进行研究,利用上面建立的温度与负荷的回归模型对负荷进行预测,预测结果与实际负荷的差值,认为是积温效应带来的负荷差,分别研究其与对应的日最大温度、日平均温度、日峰负荷对应温度的相关性,将相关性最大的温度作为积温效应研究对象。

式中:r为温度与积温效应负荷的相关性;ˉt为平均温度;Pi为第i个预测日的实际负荷;Pei为第i个预测日的预测负荷与实际负荷的差值,即为积温效应负荷,为预测负荷与实际负荷的差值的平均值。
(5)将温度修正公式(1)代入公式(2)预测第i日负荷,结合表示式(4),采用最小二乘法拟合求解最优参数(m ,n,TL,c1,c2)。
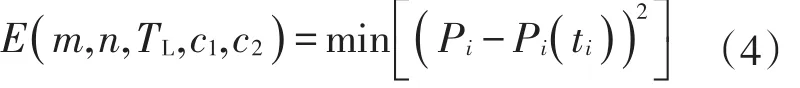
式中:E(m ,n,TL,c1,c2)为最优参数(m ,n,TL,c1,c2)所对应的误差平方和。
2 支持向量机
2.1 SVM原理
支持向量机(support vector machine,SVM)是一种基于统计理论和结构风险原则的人工智能算法。它的基本思想是:首先把输入空间的样本通过变换映射到高维特征空间中,然后在高维空间中求取把输入空间分开的最优分界面[13—14]。
2.2 SVM参数
支持向量机在实际的负荷预测中,参数的选取对预测精度有很大的影响,研究表明:核函数类型及其相关参数、不敏感损失函数ε、错误惩罚因子C对负荷预测精度影响很大。一般来说,这些参数都需要根据实际经验选取,这样既不利于支持向量机的推广使用,又很难提高负荷预测精度。因此,对支持向量机[15—16]相关参数的选取就变得十分重要了。
目前,对支持向量机相关参数的选取方法有很多,例如最小二乘法(LS)、遗传算法(GA)、粒子群算法(PSO)和模拟退火法(SA)。支持向量机相关参数的选取和优化,可使得负荷预测精度得到较大提高,因此,本文将参数优化后的支持向量机称为优化支持向量机[17—18]。
3 算例分析
考虑到日峰负荷不仅受到温度的影响,还受到日期类型的影响,例如是否是节假日和星期类型等,本文在提取历史数据时,首先将节假日(例如端午节)和周末(周六、周日)剔除掉,将剩余正常工作日的负荷作为本文的研究对象,将江苏某地区负荷数据作为历史数据(如表1所示),验证所提出方法的有效性和正确性。
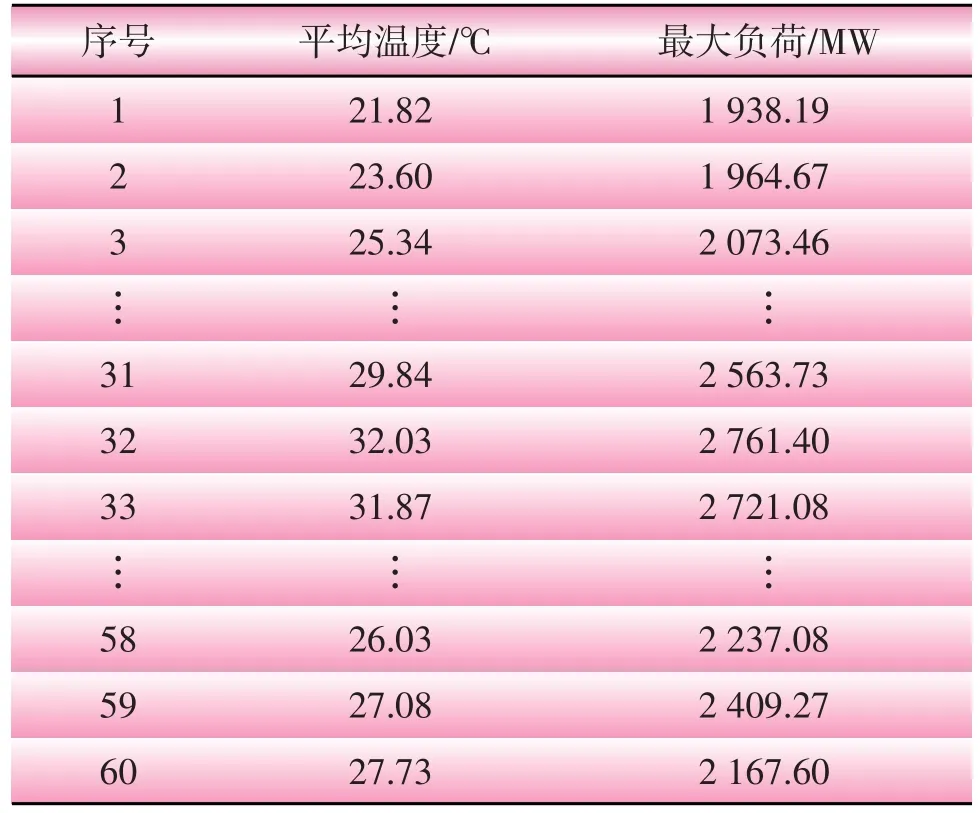
表1 温度与负荷原始数据
3.1 参数确定
(1)研究负荷与温度的相关性
表2为负荷与温度的相关性,可知平均温度与最大负荷的相关性最大,因此,将平均温度作为研究对象,建立平均温度与负荷的一元线性回归模型。

表2 负荷与温度的相关性
(2)研究积温效应负荷与温度的相关性
积温效应负荷即为回归模型预测负荷与实际负荷的差值。重复执行积温效应参数确定方法的步骤(2)得到回归模型,然后执行积温效应参数确定方法的步骤(4)得到温度与积温效应负荷的相关性,如表3所示,可知积温效应负荷与最大温度的相关性最大,因而将最大温度作为积温效应研究对象。线性回归模型参数如表4所示。

表3 积温效应负荷与温度的相关性

表4 线性回归模型参数
(3)确定积温效应参数
根据积温效应参数确定方法的步骤(5),将江苏某地区2015年6、7月正常工作日历史数据作为研究对象,代入式(4)中,采用最小二乘法并结合实际情况得到最优参数:m=5;n=5;TL=32;c1=0.017;c2=-0.29。
3.2 结果分析
(1)支持向量机预测分析
支持向量机的参数对负荷预测精度影响较大,因此,在采用支持向量机预测负荷之前,需要对核函数类型及其相关参数、不敏感损失函数ε、错误惩罚因子C进行优化选取。选用2015年6、7月修正之后的温度和负荷数据作为支持向量机的训练数据,分别采用不同的核函数及其相关参数,错误惩罚因子和损失函数对8月前10个工作日负荷进行预测,得到的预测结果如表5所示。
由表5可知:①当支持向量机核函数及其相关参数,错误惩罚因子和损失函数不同时,预测结果存在一定差异,合理的选择参数,能够极大地提高负荷预测精度;②当核函数采用spline型,损失函数采用einsensitive型时,负荷预测精度最高,达到98.33%。
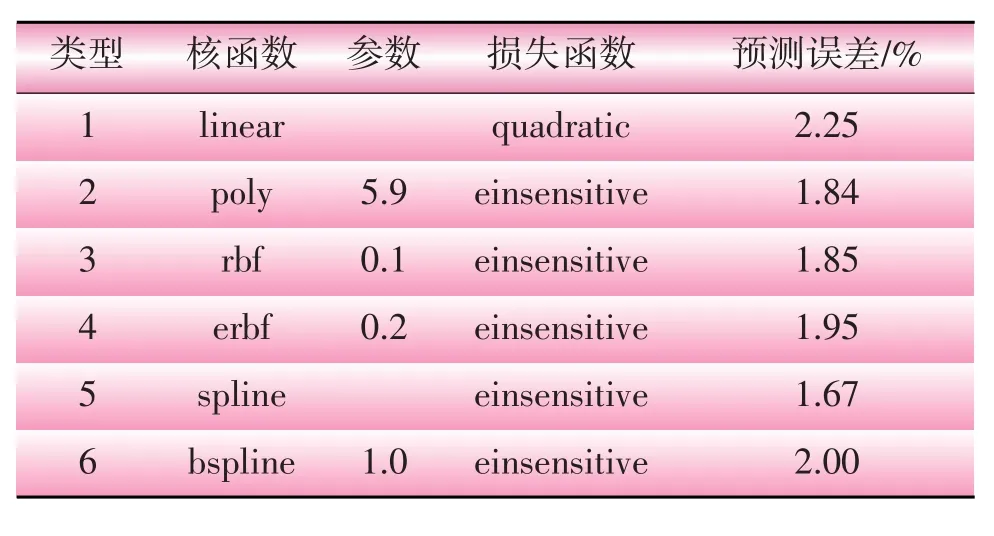
表5 支持向量机预测结果
(2)积温效应结果分析
为了验证所提出的考虑积温效应的负荷预测方法的有效性和正确性,将未经修正的温度直接代入回归模型进行预测,同时为了验证支持向量机预测负荷的有效性,将预测方法的结果进行对比分析,如表6所示。
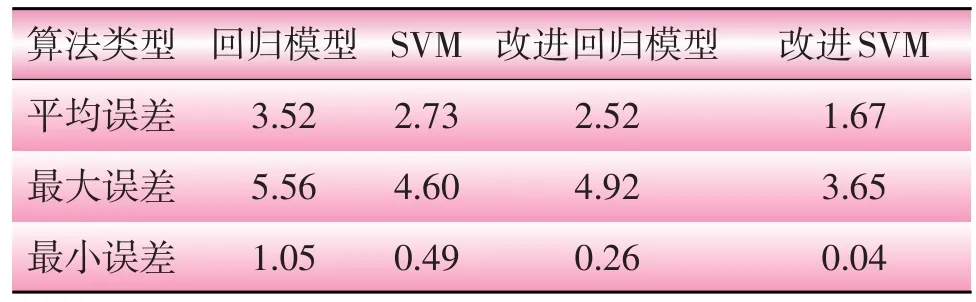
表6 考虑积温效应的负荷预测结果%
分析表6可知:①支持向量机预测负荷精度高于一元线性回归模型;②考虑积温效应的负荷预测方法预测负荷精度大幅度提高;③考虑积温效应的负荷预测方法预测效果好,预测10个工作日峰负荷平均准确率达到98.33%,最大相对误差为3.65%,而最小相对误差为0.04%,预测精度高。
为了比较直观地分析、对比预测效果,绘制了负荷预测效果图,横坐标表示10个预测工作日,纵坐标表示所对应的负荷,如图1和图2所示。
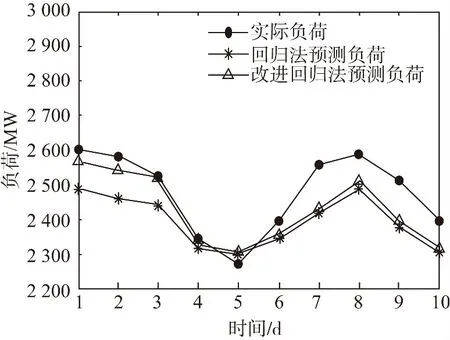
图1 回归法预测负荷结果
(3)优化支持向量机算法分析
目前,对支持向量机进行优化的算法有很多,本文将研究最小二乘法(LS)、遗传算法(GA)、粒子群算法(PSO)和模拟退火法(SA)。为了分析优化支持向量机的性能,分别采用LS-SVM,GA-SVM,PSO-SVM和SA-SVM 4种方法来预测负荷,得到预测结果如表7所示。
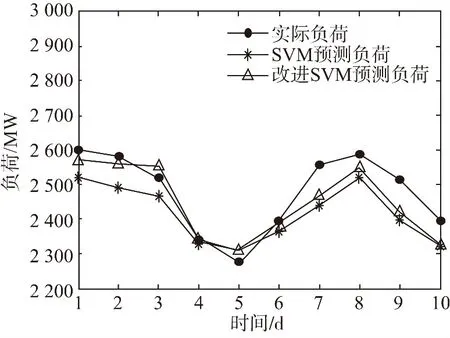
图2 SVM预测负荷结果

表7 优化SVM预测结果
分析表8可知:①优化支持向量机预测精度基本一致,因为经过优化后,核函数及其相关参数,错误惩罚因子和损失函数基本一致;②优化支持向量机对核函数及其相关参数,错误惩罚因子和损失函数进行了优化,不仅能够提高运行效率,还可以提高预测精度;③优化支持向量机的优化算法需要执行时间,不同优化算法优化时间不同,而一般的支持向量机无需优化时间,需根据实际经验选取参数;④优化支持向量机不仅能够提高运行效率,还可以提高预测精度。在选择优化算法时应该充分考虑优化时间,从表7中可知最小二乘法优化支持向量机优化时间最短,因为优化支持向量机时需要优化的参数较少,相对比较简单,而其他方法优化的参数较多,例如GA-SVM需要选择遗传算法的群体大小、终止进化代数、交叉概率以及变异概率等参数;PSO-SVM需要选择粒子群算法的种群粒子数、最大迭代次数以及学习因子等参数;SA-SVM需要选择模拟退火法的初始温度、抽样次数以及降温率等参数。选择最小二乘法来优化支持向量机,无需遗传算法、粒子群算法和模拟退火法等智能算法。
4 结束语
随着电力负荷对气象因素敏感程度的增加,气象因素对负荷的影响也越来越大,因此预测负荷时考虑积温效应是十分有意义的。研究了积温效应的2种表现形式,分别为多日积温效应和2日积温效应,根据它们的特点,提出了考虑积温效应的温度修正方法。提出了考虑积温效应的优化支持向量机负荷预测方法,并借助历史负荷数据验证了该方法的正确性和可行性。D

