管壳式换热器传热温差的优化及影响分析
张乾坤,周 琴,李 健
(1.安徽华东化工医药工程有限责任公司上海分公司,上海 201315; 2.上海华西化工科技有限公司,上海 201315)
化工装置节能中最重要的一环是对冷热流体进行能量的回收与利用,换热器在化工生产装置能量回收中充当了重要的角色。针对具体的化工装置,由于工艺加工过程的需要,可能有多股冷流被加热和多股热流需要被冷却的需要。若将这些冷流与热流根据温位高低进行合理的匹配,将需要冷却的热流体去加热需要被冷却的冷流体,就可以减少热公用工程(燃料气、蒸汽、导热油等)及冷公用工程(循环水、冷冻水等)的消耗,从而节约了能源。
针对换热网络优化的方法主要有加点分析法、数学规划法及随机优化法[1],目前应用较多的为夹点分析法,此方法为Linnhoff首次提出,主要应用热力学第一及第二定律,在给定的传热温差△T下,求解特定的换热网络使得其有最小公用工程消耗、最小换热面积或者年投资费用。而传热温差在该方法中需要提前给定,而针对特定的换热网络其会有一个优化值。如图1所示,随着传热温差缩小,换热网络中回收的热量增加,意味着减少了冷热公用工程消耗,但同时所需的总传热面积增大,进而设备制造费及占地面积增大。如果综合考虑制造费用及公用工程操作费用,传热温差应有最优值,对应着换热网络的最小总费用。
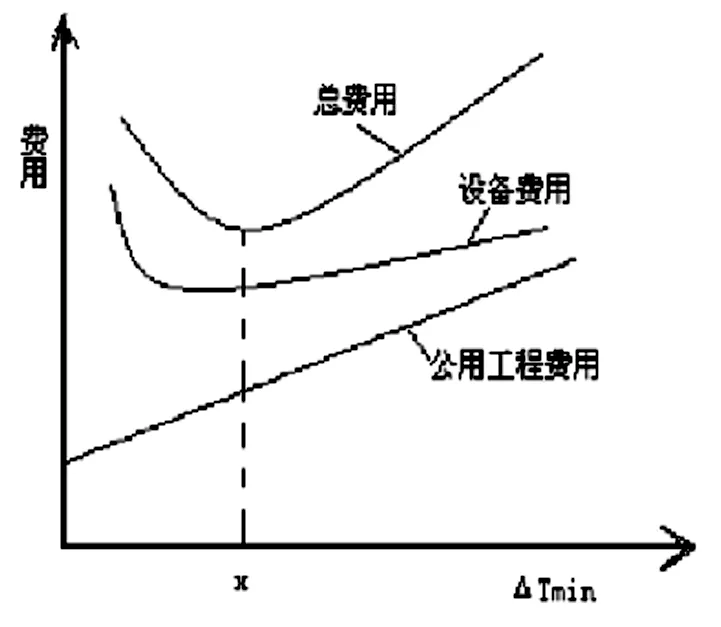
图1 传热温差与总体费用关系
1 模型的描述
传热温差对总费用的影响因素比较复杂,为分析其影响因素对换热网络进行简化,考虑典型的换热网络(如图2所示),假设根据工艺过程需要,一股热流体需要从温度T1冷却到终温T3,同时一股冷流体需要从温度t1加热到t3,为回收热量将冷热流体先经换热器E1换热分别到达t2及T2,然后分别经换热器E热及E冷,分别与热及冷公用工程介质再换热到各自所需要达到的终温t3与T3。其中E热根据需要可以选择加热炉或各种压力等级的蒸汽加热器或者导热油换热器等,E冷也可以根据终温及介质特性选择是空气冷却器或循环水冷却器、冷冻水冷却器等。
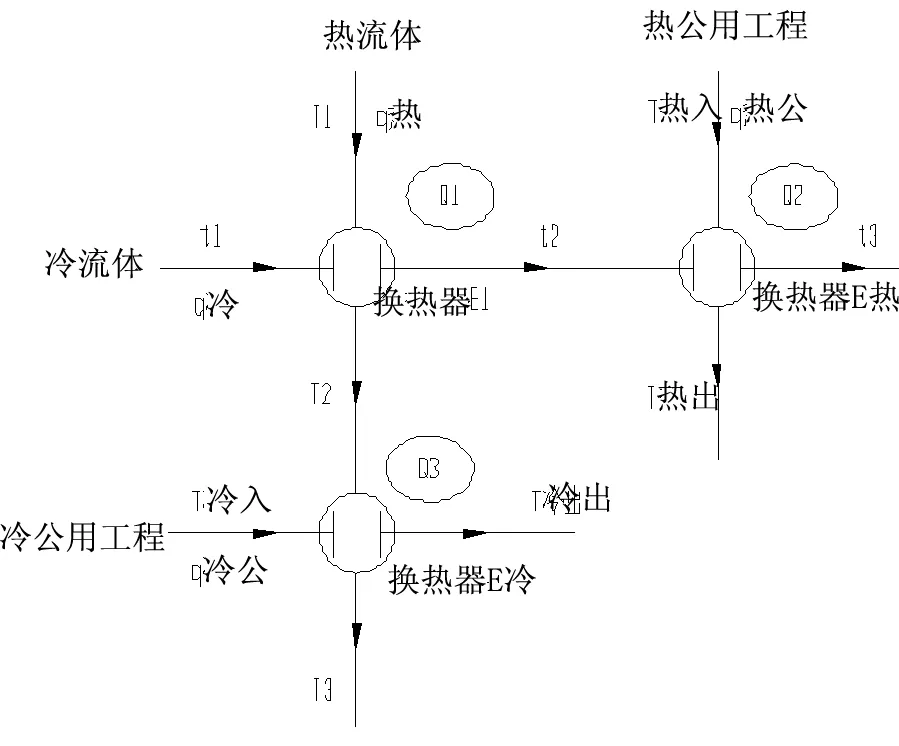
图2 换热流程示意图
针对E1,假设其为常见的管壳式换热器,冷热流体均无相态变化,且冷热流体比热容不随温度变化。根据基本传热方程可得如下基本公式1-2[2]。
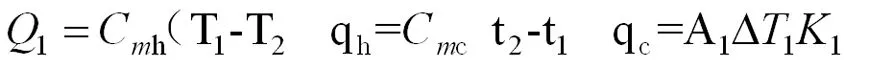
(1)
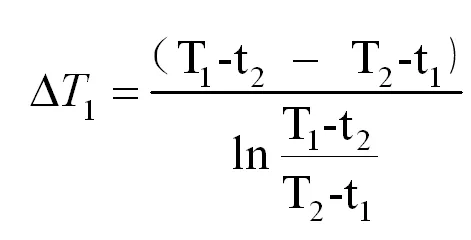
(2)
式中:Q1——换热量,J;Cmh——热流体比热,J/kg℃;Cmc——冷流体比热,J/kg℃;qh——热流体质量流率,kg/h;qc——冷流体质量流率,kg/h;A1——换热面积,m2;△T1——对数平均传热温差,℃;K1——换热器总传热系数,kJ/m2℃。
上式中t2为自变量,其值的变化会影响回收的传热量及所需的传热面积。针对管壳式换热器,在冷热流体质量流率一定的情况下,假设换热器壳径不变,则管壳程流体平均流速不变,则总传热系数K1也不变。此时换热器面积的变化体现在管束的长短变化上,进而影响换热器的重量和制造费用。则有如下制造费用的近似关联式。
F1=B1A1
(3)
式中:F1——制造费,元;B1——面积费用系数,元/m2;
同理针对换热器E冷与E热,有类似关系式见式4-9;三台换热器总费用F为总系数之和,见式10;操作费用为冷热公用工程费用的总和。归结为式11。
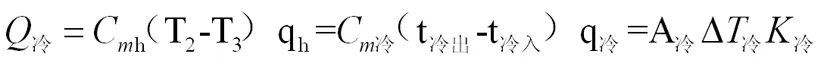
(4)
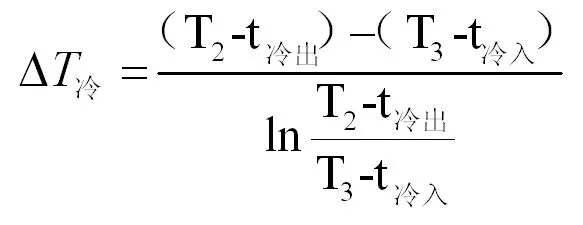
(5)
F冷=B冷A冷
(6)
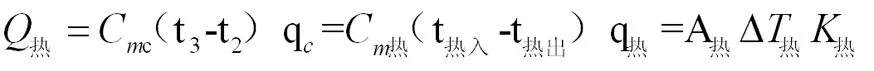
(7)
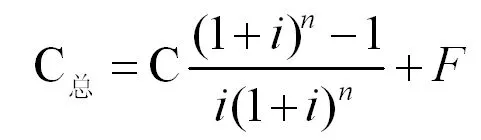
(8)
F热=B热A热
(9)
F=F冷+F热+F1
(10)
C=C冷+C热=(q冷f冷+q热f热)H
(11)
式中:Q冷——冷公用工程换热量,J;Cm冷——冷公用工程介质比热,J/kg℃;q冷——冷公用工程介质流率,kg/h;A冷——冷却器换热面积,m2;△T冷——冷却器对数平均传热温差,℃;K冷——冷却器总传热系数,kJ/m2℃;Q热——冷公用工程换热量,J;Cm热——冷公用工程介质比热,J/kg℃;q热——冷公用工程介质流率,kg/h;A热——冷却器换热面积,m2;△T热——冷却器对数平均传热温差,℃;K热——冷却器总传热系数,kJ/m2℃;F冷——冷却器制造费,元;B冷——冷却器面积费用系数,元/m2;F热——加热器制造费,元;B热——加热器面积费用系数,元/m2;f冷——冷公用工程价格,元/kg;f热——热公用工程价格,元/kg;C——年操作费用,元;H——年操作时长,小时。
参考技术经济评价,对该换热系统采用年总费用法进行费用计算[3]。装置总运转寿命(n)按15年考虑,行业基准收益率(i)按12%选取。则总体15年的总费用C总计算见式12。
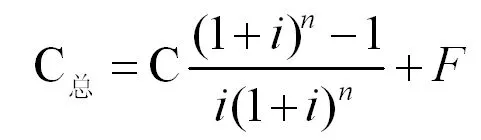
(12)
式中:i——基准收益率,%;n——装置总运转年数。
2 最优化求解方法
综合式1-12,冷热流体工艺所需温度T1、T3、t1、t3已知;Cmc、Cmh、Cm冷、Cm热等流体介质热力学物性可根据介质查到;t冷入、t冷出、t热入、t热出为界区所供的冷热公用工程介质的已知量;K1、K冷、K热可根据具体冷热流体介质取经验的传热系数;B1、B冷、B热可根据标换管壳程压力等级及材质拟合出相应的参数库进行选取(数据可参考中石化标准换热器样本);f冷、f热为冷热公用工程介质的价格(可根据经验选取)。除以上常量以外C总可换算为t2或者T2的函数,即为C总=f(t2)。
f(t2)具体关系式可用数学符号计算软件(Maple)进行计算[4],由于所计算的符号公式较为复杂,不便于求解其符号最优值。而工程计算中一般仅关心具体的数值解。此时可以用擅长于数值求解的Matlab进行求解,由于该函数为非线性函数,可已用Matlab优化工具箱中的Fminbnd函数进行求解[5]。其求解表达式如下:
X=Fminbnd(Fun,x1,x2),其中Fun是待求最小值函数,可以为表达式或自定义函数名称,这里Fun设置为f(t2)的具体符号表达式,要求解在(x1,x2)区间范围下的最优解X。求解的根当中需要注意的是,有实际意义的t2须满足换热器传热极限的限制,即将t2代入式1后,必须满足T2>t2及T1>t1。
3 影响因素分析
由式1-12可知,影响最终的操作费用的因素较为复杂,具体的常量系数又要根据要回收热量的冷热流体特性及要选用的冷热公用工程介质特性做出不同的选择。因此其最优值并非固定不变的。但考察以上各式,可得到换热网络中各参数的变化对最优传热温差变化方向及敏感程度的影响。
综合式1-12,影响传热温差的主要因素可分为三大类,一是传热流体的物性,主要是流体的总传热系数;二是冷热公用工程介质价格及其与流体配对的总传热系数;三是冷热流体的温度压力及组成特性,其决定了换热器材质及壁厚等。
为考察以上三个方面对最优传热温差的影响,分别固定其中两个因素,对另外一个因素进行计算分析。固定一个换热流程,首先计算对比了三对不同的传热流体介质(石脑油、柴油及蜡油)的最优传热温差,此时冷公用工程介质选择循环水冷却、热公用工程介质选择导蒸汽加热,通过第2节所述方法进行计算,发现油品越轻最优传热温差降低;这是因为油品越轻其粘度越小,雷诺数容易落在紊流区间,导致传热系数较高,同样的换热面积下其传热温差可以取较小值,故倾向于多换热,导致最优传热温差减小。
其次通过固定换热冷热流体均为石脑油,变换冷却介质及加热介质为价格更贵的冷冻水及更高热品位的中压蒸汽后,f冷及f热系数增大,最优传热温差也趋向缩小,这说明需要通过更多的回收热量来减少昂贵的公用工程介质消耗。
最后通过提高石脑油换热器的操作压力,导致换热器的材质及壁厚升高,反映在系数B1、B2、B3均有提高,则最优传热温差趋向于提高,但提高量不太明显。这是由于温差提高后虽然导致了冷热流体换热面积的减少了,但是会增加冷热公用工程换热量的增大,由于公用工程介质的温位普遍较高,冷热公用工程两个换热器的传热温差变化不敏感,进而导致冷热公用工程换热器面积按比例增加,故的设备制造总费用反而增加。
由以上可知三类类因素中,换热流体特性及公用工程介质特性对传热温差的影响较为敏感,而换热器的材质及壁厚对传热温差在一定范围内有影响,影响程度不太敏感。
4 结论
针对简化的换热网络,根据基本的传热方程及技经分析,得出影响管壳式换热器最优传热温差的各个因素,并给出量化计算最优传热温差的数学方法。通过分析各个影响因素,找出对其影响较大的换热流体传热系数及公用工程价格的关键因素。
虽然该模型是针对简单的换热网络进行建模,但是对于复杂换热网络系统,其最优传热温差的影响因素具有参考意义,可以利用成熟的夹点分析,结合计算所得的最优传热温差,设计出最优的换热方案来,为换热系统的优化提供设计基础及调整方向。所需注意的是本模型是针对管壳式换热器进行分析,如换热器类型变化,需调整为特定换热器的传热方程式,但仍可按此方法得到最优传热温差值。

