植物根底害虫治理控制模型研究
王铁英,左 萍,蔡 瑾
(中国人民公安大学 信息技术与网络安全学院,北京 100038)
0 引言
近年来,地下害虫发生和危害日趋严重,给农业生产造成重大损失,所以对地下害虫的治理控制越来越受到人们的重视[1].在植物根底的土壤中常存在一种以土壤中微生物为食的害虫,它的存在对植物根系增长造成极大的危害,必以农药杀之.当然农药也会对土壤微生物造成一定的损害,我们要通过了解害虫发生的状态来控制用药量,使害虫得到控制并且保证土壤微生物保持正常生长进而有益于植物生长.害虫防治是一个生态学问题,防治害虫的目的不是单纯地追求直接消灭防治对象,而是为了控制种群数量,使其对作物不足以造成危害.当害虫的数量达到经济阈值(Economic Threshold, ET)的时候,通过喷洒农药来控制害虫的数量,不让其超过经济危害水平(Economic Injury Level, EIL).目前,应用文献[2]中提出的半连续动力系统的理论和方法研究害虫治理,已有很多报道[3-8].
本文针对植物根底害虫建立如下具有状态反馈控制治理害虫模型:
(1)
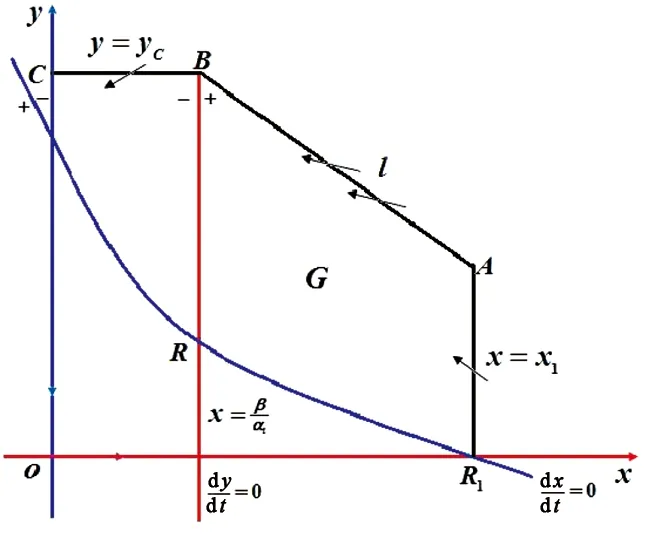
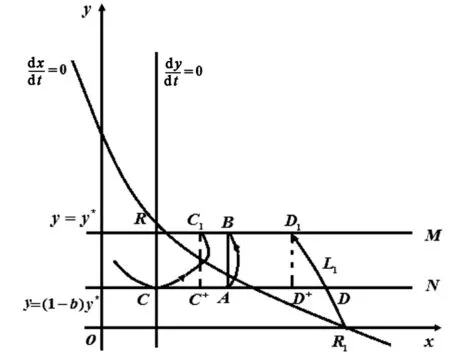
其中:x和y是t时刻土壤中微生物和害虫的密度;r>0是x的内禀增长率;ω>0为半饱和常数;α,α1是正常数;β>0是害虫的死亡率;0 (2) 利用系统(2)所对应的线性系统,不难判定O为鞍点,当正平衡点存在时R1也必为鞍点;正平衡点R(x2,y2)是稳定的结点或焦点. 取Dulac函数B(x,y)=x-1y-1,容易算得 定理1 若 (3) 证明根据环域定理,构造外境界线.当y>0时,由于 故当轨线与x=x1相遇时,均从直线x=x1的右方穿入左方(如图1所示).考察直线 l≜y+(x-x1)-y1=0. 由于 (α-α1-1)x2+(β+α1x1-αx1)x+ 只需选取 y1>max{((α-α1-1)x2+(β+α1x1-αx1)x+ 故当轨线与y=yC相遇时,均从直线y=yC的上方穿入下方. 图1 有界域Fig. 1 Bounded domain 定理3 若0 图2 当0 (2)稳定性:由上述阶1周期解存在性的推导过程及系统(1)的几何结构(图1和图2),可以知道系统(1)的阶1周期解为单侧渐近型凸闭阶1周期解,利用定理2和参考文献[9]中的定理5.19的推论5.3研究系统(1)的阶1周期解的稳定性. 对于系统(1),我们计算 符号不确定,构造Dulac函数B(x,y)=x-1y-1,在区域G′={(x,y)|x>0,y>0}内连续、可微,系统(1)化为 (4) 对系统(4)有 由参考文献[9]中定理5.19的推论5.3可知系统(1)的阶1周期解是轨道稳定的.证毕. 本文研究了一类带有脉冲状态反馈控制的植物根底害虫治理模型的动力学行为. 首先分析了无脉冲控制系统(2)的动力学性质,此系统在第一象限内不存在极限环,正平衡点R(x2,y2)是全局渐近稳定的.从生态意义上来说,若经济临界值y*>y2,由正平衡点的全局稳定性,害虫种群与微生物种群最终将稳定在正平衡点R(x2,y2)的位置上,所以在这种情况下害虫种群的数量永远不会达到经济危害值. 其次证明了当y*1 无脉冲系统的定性分析
1.1 系统(2)的奇点分析
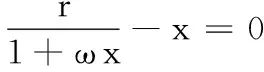
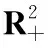
1.2 确定无环区域

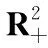
1.3 全局渐近稳定性
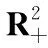
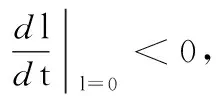
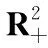
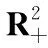
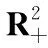
2 系统(1)周期解的存在性与稳定性
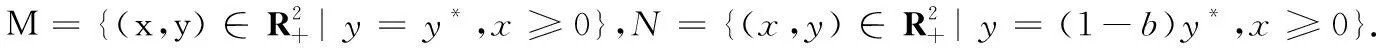
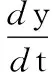
3 结论

