结合SPA和PLS法提高冬小麦冠层全氮高光谱估算的精确度
白丽敏,李粉玲,常庆瑞,曾 凤,曹 吉,芦光旭
(西北农林科技大学资源环境学院,陕西杨陵 712100)
氮素是作物生长发育、产量以及品质形成的主要营养元素,掌握作物关键生育期的氮素丰缺状况是指导农业生产科学施肥、作物长势监测以及产量预报的先决条件。利用现代高光谱遥感技术进行作物氮素含量的快速、无损、准确监测是当前精准农业研究的重要领域[1–3]。研究表明利用单一敏感波段构建作物氮素含量的估算模型精度较差,利用多个敏感波段以及敏感波段之间的组合构建光谱指数能有效减少土壤环境和大气条件对冠层光谱的影响,进而提高模型的预测精度[4–7],如Wright等[5]建立了基于归一化植被指数 (NDVI) 和归一化绿波段差值植被指数 (GNDVI) 的小麦叶片氮素含量二次多项式估算模型;冯伟等[6]、胡昊等[7]研究表明红边位置参数与叶片氮含量可达到极显著水平,可以利用REPIE、SDr-SDb和FD729等参数对小麦叶片氮含量进行监测。但是,这些单一敏感变量仅利用了全光谱信号的部分敏感波段,而忽略了冠层高光谱连续信号中其他有效敏感波段对叶片氮含量的贡献。因此,如何充分利用冬小麦冠层全波段光谱信息来进一步优化小麦氮素定量分析模型是当前的研究热点,如杨宝华等提出的竞争性自适应重加权算法与相关系数法相结合的算法,就从2151个原始波段中选出了30个敏感波段建立了精度更高的小麦氮含量预测的非线性回归模型[8],但该模型不仅复杂,且所筛选的变量之间的相关性较高。
连续投影算法 (SPA) 是一种使矢量空间共线性最小化的前向变量选择算法 (该算法的迭代原理以及具体步骤参见文献[9]) 。它能够从全波段光谱信息中筛选出具有最低信息冗余度的光谱变量,保证所选择的特征波段之间共线性最小,从而减小模型建立过程中的拟合复杂程度,加快拟合运算速率。同时该算法所筛选出的敏感特征波段具有重要性顺序,能直接反映所筛选变量与因变量之间的定量关系,因此在高光谱信息的研究中得到广泛关注[10]。但该算法在作物氮素营养监测中的应用还未见报道。本研究旨在利用冬小麦冠层全波段光谱信息,结合连续投影算法 (SPA) 筛选冬小麦拔节期冠层光谱对叶片氮含量的敏感特征波段,并结合偏最小二乘 (PLS)技术,进行冬小麦拔节期的叶片氮含量估算,以期为冬小麦关键生育期氮素含量的遥感估算提供理论依据和技术支持,为冬小麦后期生长的田间管理提供科学的指导性建议。
1 试验设计与信息采集
1.1 试验设计
本研究冬小麦种植小区试验在陕西省咸阳市乾县三合村开展,土壤类型为红油土,质地为壤土,土壤基本肥力状况为:土壤有机质13.36 g/kg、全氮0.48 g/kg、有效磷13.54 mg/kg、速效钾182.88 mg/kg、速效氮44.86 mg/kg。供试品种为关中地区常见品种‘小偃22’。试验共设36个试验小区,每个小区面积为36 m2(6 m × 6 m) 。试验设计氮 (N)、磷(P)、钾 (K) 3种养分处理,6个施肥梯度,每个梯度设置2个重复。氮肥标准施入量为150 kg/hm2,施肥梯度为不施氮、1/4标准氮 (严重缺氮)、1/2标准氮(缺氮)、3/4 标准氮 (少量缺氮)、标准氮 (适宜氮) 和5/4 标准氮 (过量氮),记作 N0、N1、N2、N3、N4、N5,肥源为尿素 (纯氮含量为46%) 。磷处理与钾处理均施纯氮75 kg/hm2,养分试验设置梯度与氮肥相同。磷肥试验不施钾肥,磷肥标准量为90 kg/hm2,6 个梯度记为 P0、P1、P2、P3、P4、P5,肥源为过磷酸钙。钾肥试验不施磷肥,标准钾肥施入量为60 kg/hm2,施肥梯度记作 K0、K1、K2、K3、K4、K5,配施肥料硫酸钾。各肥料作为底肥一次施入,不追肥,田间管理按大田管理方式进行。
1.2 冠层高光谱和叶片全氮测定
在冬小麦拔节期,选择晴朗无风的天气,利用便携式非成像全光谱地物波谱仪 (SVC HR-1024I,SVC) 在10:30—14:00之间进行冬小麦冠层光谱测定。SVC可获取目标地物在350~2500 nm波长范围内1024个波段的光谱数据,其中350~1000 nm波段范围内光谱分辨率 ≤ 3.5 nm,采样间隔1.5 nm;1000~1850 nm波段内光谱分辨率 ≤ 9.5 nm,采样间隔1.5 nm;1850~2500 nm波段内光谱分辨率6.5 nm,采样间隔2.5 nm。测量前进行标准白板校正,观测时传感器垂直向下,距离冠层130 cm,视场角25°,设置1次采样重复10次,以其平均值作为该观测样点的光谱反射率。每个小区均匀采集3个样点,以样点光谱数据的平均值作为该样区的冠层光谱反射数据。测定光谱的同时选取有代表性小麦植株20株,采集其叶片带回实验室杀青、烘干、粉碎,称取0.2 g左右干样,用浓H2SO4在有催化剂的条件下消煮,采用凯氏定氮法测定叶片全氮含量。
2 数据处理与建模方法
2.1 冠层光谱数据预处理
高光谱数据蕴含着丰富的地物反射信息,同时也包含了大量的噪声,严重影响了地物反射光谱中的吸收特征,降低了数据的分析精度[11]。本研究首先将冠层光谱重采样为3 nm,对重采样后的光谱数据进行Savitzky-Golay (SG) 平滑处理,剔除了光谱曲线上的细小噪声,提高光谱数据的信噪比。
2.2 氮含量估算理论与方法
2.2.1 叶片氮含量遥感估算原理 构成健康绿色植物的生物化学成分主要包括叶绿素和其他色素 (胡萝卜素和叶黄素等)、水、蛋白质、淀粉、蜡、木质素和纤维素等结构化的生物化学分子。当植物体内某些营养元素缺乏或者过量时,造成植株体内相关生物化学成分的变化,从而引起对该类生化成分敏感的冠层光谱曲线吸收波段出现波动[12]。植被生化组分遥感监测的关键就是筛选对这些变化敏感的光谱波段[13]。作物氮素含量高光谱估算就是基于对氮素组分敏感的反射光谱或吸收光谱以及光谱指数,探寻其与氮含量之间的定量关系[14]。
2.2.2 叶片氮含量估算方法 偏最小二乘回归 (PLS)兼具了主成分分析、多元回归和典型相关分析的优点,在最大限度消除变量之间共线性的同时,保证各主成分对因变量具有最好的解释性,从而取得最佳的建模精度和更好的估测效果[15–16]。本研究首先在MATLAB环境下,通过编程实现基于SPA算法的冬小麦拔节期叶片氮含量敏感特征波段的提取,基于这些敏感波段反射率,在MATLAB软件中采用偏最小二乘 (PLS) 回归法进行叶片氮含量的估算建模。
2.3 建模和检验样本提取
试验获得研究区2015—2016年冬小麦拔节期冠层光谱和叶片氮含量有效样本56个。冬小麦拔节期叶片氮含量最小值为1.26%,最大值为3.25%,平均值为2.53%。将样本数据依据叶片氮含量实测值的大小进行排序,按照5∶1抽取45个样本作为建模集,11个样本作为验证集,建模集和验证集样本数据均服从标准正态分布。
2.4 模型精度检验指标
本研究采用决定系数 (R2)、均方根误差(RMSE)、相对预测偏差 (RPD) 和相对预测误差(REP) 4个指标进行模型检验,其计算公式见参考文献[17]。当R2和RPD的值越大,RMSE和REP的值越小,说明模型精度越高。其中RPD的评价标准采用Chang等[18]提取的阈值划分方法,RPD > 2.0表明模型拥有极好的预测能力;1.5 < RPD < 2.0表明是可以接受的模型,且模型能够粗略估测样本;RPD <1.5表明模型不具备预测能力。
3 结果与分析
3.1 基于SPA算法的特征波段提取
本研究中冠层光谱的范围为338~2510 nm,共包含725个波段。利用连续投影算法,在MATLAB中对重采样和平滑预处理后的全波段冠层高光谱数据进行叶片氮含量的敏感特征波段提取。经重复抽样和检验,在RMSE达到最低值0.08时,优选出了冠层光谱对叶片氮含量敏感的8个特征波段,光谱波段数目下降了98.9%。优选出的特征波段按照重要性顺序分别为1985 nm、2474 nm、1751 nm、1916 nm、2507 nm、1955 nm、2465 nm和344 nm。这些敏感特征波段反射率与叶片氮含量的相关性如表1所示,各入选敏感特征波段反射率与叶片氮含量均呈负相关关系,并且都通过了0.01水平的显著性检验,其中344 nm的相关系数绝对值最高为0.83,1916 nm的相关系数绝对值最低为0.36。按照优选特征波段的顺序,各特征波段反射率与叶片氮含量的相关性呈现先下降后逐渐上升的趋势。
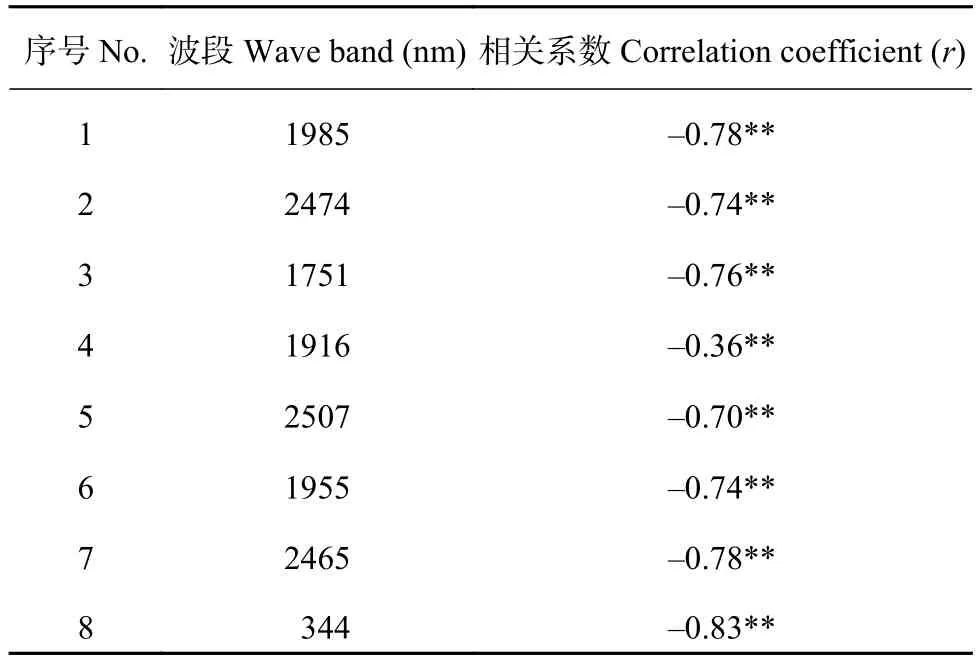
表1 敏感特征波段反射率与叶片氮含量的相关性Table 1 Correlation between reflectance of sensitive bands and leaf nitrogen contents
3.2 基于PLS的叶片氮含量估算
将连续投影算法优选出的8个敏感特征波段作为模型的输入变量,实测叶片氮含量作为响应变量,利用PLS进行叶片氮含量的预测建模,预测方程为:
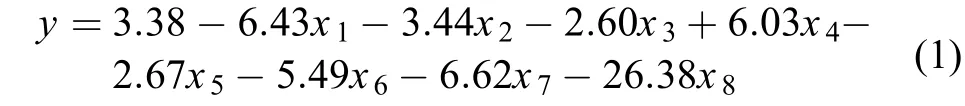
式中,xi为筛选出的敏感特征波段的反射率;i为敏感波段所对应的序号。所建PLS模型的决定系数为0.82,建模的均方根误差为0.28,表明预测方程具有较高的估算精度。所建PLS回归模型各变量的标准化系数依次为–0.14、–0.07、0.12、0.15、–0.05、–0.11、–0.13和–0.28。一般情况下,估算模型标准化系数的绝对值越大,说明该变量对模型的贡献性越大,其中344 nm波长反射率的贡献性最大,2507 nm波长反射率的贡献性最小。总体上,按照敏感特征波段的优先顺序,各敏感特征波段所对应标准化系数的绝对值先下降后上升,与敏感特征波段与叶片氮含量的相关性变化趋势相同。
3.3 基于PLS的叶片氮含量估算模型检验
利用检验样本对敏感特征波段反射率建立的PLS回归模型进行精度检验,验证集中的实测值与预测值的拟合决定系数为0.84,均方根误差为0.21,预测相对误差为0.09,预测相对偏差为2.45,表明通过SPA结合PLS方法建立的敏感特征波长与叶片氮含量之间的多元回归模型具有极好的样本预测能力。实测值与预测值的空间分布如图1所示,模拟方程的斜率为0.98,接近于1∶1线。
3.4 基于常用植被指数的叶片氮含量估算
为了更好地检验本研究中叶片氮含量估算模型的精度,本研究基于常用的植被指数构建冬小麦叶片氮含量的估算模型 (表2),与本研究中的PLS回归进行对比。
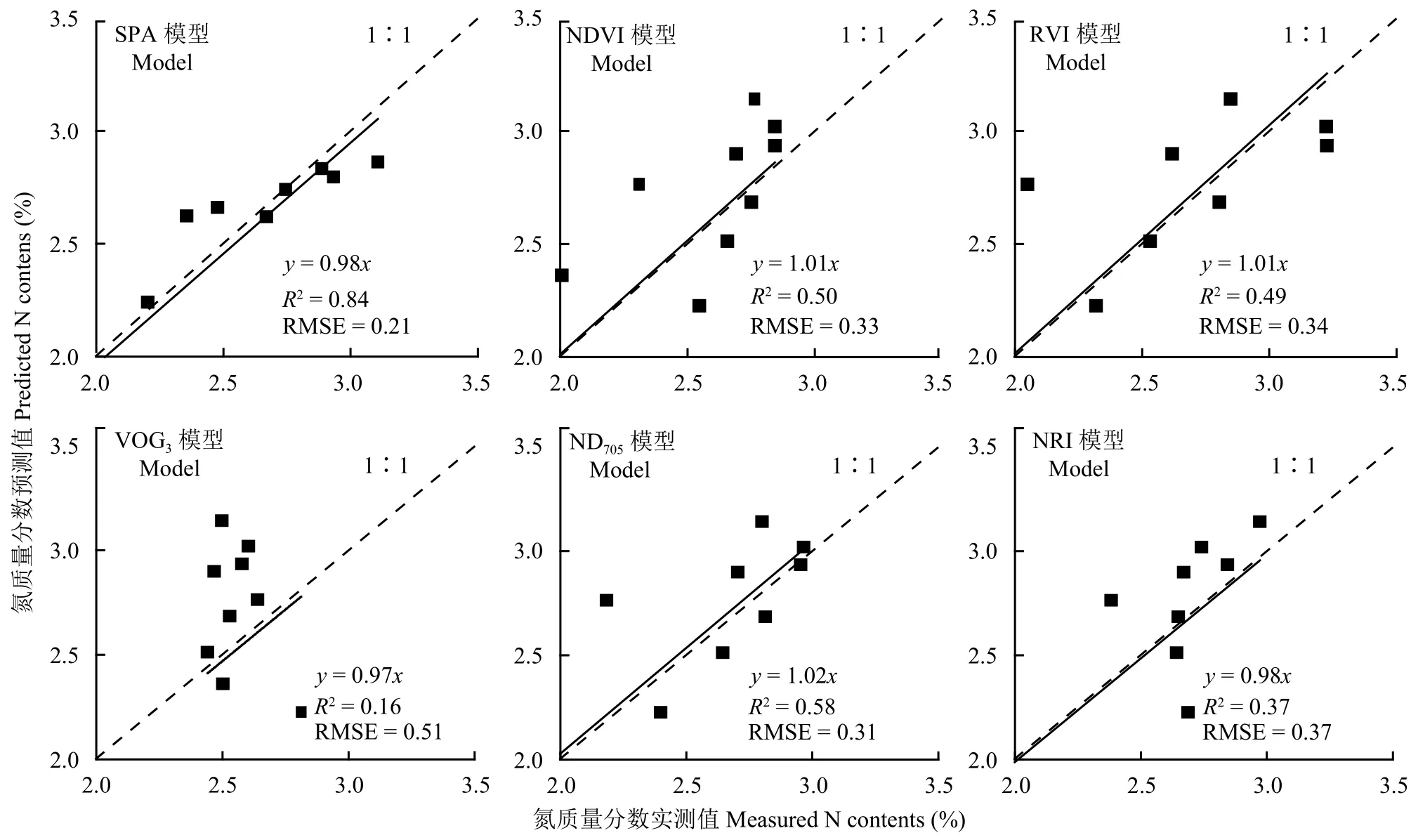
图1 不同模型冬小麦叶片氮含量预测值与实测值相关性Fig. 1 Correlation of the measured leaf nitrogen contents with the predicted ones using different models

表2 植被指数及其计算公式Table 2 Typical vegetation indices and expression
3.4.1 基于植被指数的叶片氮含量估算 本研究所选植被指数中除了VOG3之外,其他植被指数与冬小麦拔节期叶片氮素含量的相关系数均高于绝对值0.7,并均通过了0.01水平的显著性检验,其中ND705与叶片氮含量之间的相关系数最高为0.90。利用以上植被指数进行冬小麦叶片氮含量的估算模型构建 (表3)。5类植被指数对叶片氮含量的估算都更适合采用线性回归模型表达,其中基于ND705的估算模型拟合决定系数最高,为0.81;VOG3的模型拟合决定系数最低为0.34,5类模型建模的均方根误差在0.22~0.48之间。
3.4.2 基于植被指数估算模型的检验 对基于植被指数的冬小麦叶片氮含量估算模型进行检验,结果如图1所示和表4所示。相对于建模精度,各模型检验结果的拟合方程决定系数略有下降,其中基于ND705的叶片氮含量估算模型的检验结果最佳,R2为0.58,RMSE为0.31,REP为0.12,RPD为1.61,1.5 < RPD < 2.0表明该指数所建立的估算模型具有粗略估测样本的能力;VOG3检验的R2最小为0.16,RMSE为0.51,REP为0.20,RPD为 0.97,且RPD小于1.5,表明该指数所建立的估算模型没有样本估测能力。
3.5 模型精度对比
本研究所涉及的各类估算模型的检验结果如表4所示。基于植被指数的叶片氮含量估算模型中以ND705表现最佳,该植被指数与叶片氮含量的相关系数最大,为0.90,估算模型的决定系数为0.81。基于ND705植被指数的叶片氮含量估算模型检验效果也最佳,其检验样本实测值与预测值的拟合决定系数 (R2) 最高,为0.58,检验方程的RMSE最小,为0.31。基于ND705植被指数叶片氮含量估算模型的RPD为1.61,RPD值大于1.5小于2,且具有较大的决定系数和较小的均方根误差,依据本研究所参照的模型精度评价标准,这一植被指数对冬小麦叶片氮含量的估算模型可以判断为具有粗略估测样本的能力。而基于NDVI、RVI、VOG3和NRI四类植被指数对冬小麦叶片氮含量估算模型检验的RPD值均小于1.5,决定系数较小且均方根误差较大,认为这四类植被指数与冬小麦叶片氮含量之间所建立的线性回归模型不具备样本预测能力。
SPA结合PLS建立的冬小麦叶片氮含量估算模型的拟合决定系数为0.82,均大于植被指数所建模型的拟合决定系数。SPA结合PLS的估算模型在模型精度检验中,检验方程的决定系数较植被指数估算模型更高,且均方根误差更小,模型评价指标RPD值大于2 (RPD = 2.45),说明估算模型具有极好的样本预测能力。通过验证集中估算模型实测值与预测值的空间分布来看,SPA结合PLS模型的估算值与实测值的空间分布更接近于1∶1线。综上所述,通过SPA方法优选敏感特征波段,建立基于PLS回归法的叶片氮含量估算模型的精度显著提高,模型具有更好的样本预测能力。
4 讨论
由于冬小麦在不同生育期的氮吸收存在差别,其氮素积累量在起身后开始增加。小麦生育期中拔节期是最为关键的时期,拔节期小麦氮素积累量占总积累量的近一半[19],对拔节期小麦生长状况的监测可以为小麦后期生长的田间管理提供有效的指导性建议。
基于连续投影算法优选出的敏感特征波段,剔除了不相关、低贡献的波长变量,能够在很大程度上避免光谱波段信息的重叠,偏最小二乘回归方法进一步对特征波段进行主成分提取,提高了敏感特征波段与叶片氮含量之间的相关性,保证了各主成分对叶片氮含量具有最好的解释性,所构建的回归模型能较好地解释敏感特征波段对冬小麦叶片氮含量估算的贡献性。本研究通过模型精度对比发现,连续投影算法和偏最小二乘方法相结合所构建的叶片氮含量估算模型要优于基于常用植被指数的估算模型。与现有的模型对比,本研究建立的模型预测能力显著高于李粉玲等[12]以550—770 nm波段的吸收峰总面积建立的叶片氮含量指数估算模型,优于肖春华等[20]利用小麦冠层光谱角算法建立的叶片氮素估算模型。虽然杨宝华等[8]提出的估算方法精度更高,但该方法所筛选的敏感波段相关性较大,而本研究所筛选的变量个数明显下降,变量之间的相关性和信息冗余度降低,模型结构更加简洁。

表3 基于植被指数的叶片氮含量的预测模型Table 3 Prediction models of leaf nitrogen contents based on vegetation indices
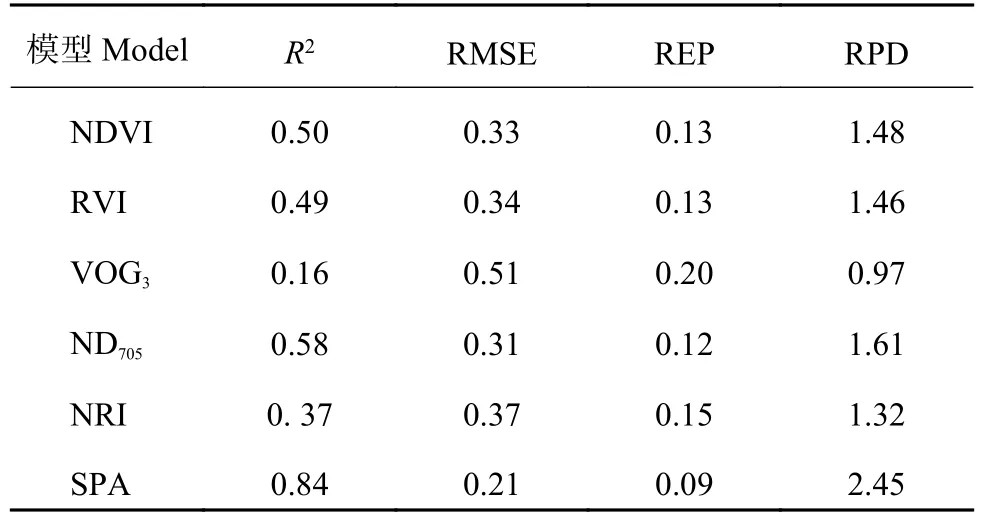
表4 冬小麦叶片氮含量的估算模型检验Table 4 Tests of leaf nitrogen content prediction models
研究表明,SPA方法最大的优点就是在消除波长变量之间共线性的同时,保证了所筛选变量对估算变量的贡献性[21]。但是该方法筛选变量的过程可能会将光谱信息中的部分有效信息剔除,或者引入一些与估算变量相关性并不高的波长变量[22],在本研究中优选出的1916 nm敏感特征波长与叶片氮含量的相关性虽通过了0.01水平的显著性检验,但相关性较低。本研究中所筛选出的叶片氮含量敏感特征波段虽然都与叶片氮含量有着较高的相关性,但其物理意义仍有待探讨。另外,本研究基于冬小麦的冠层光谱信息进行了拔节期叶片氮含量的估算研究,取得了较高的估算精度,但是该方法在其他生育期对叶片氮含量的估算能力有待检验。
5 结论
本文利用连续投影算法进行拔节期冬小麦叶片氮含量敏感特征波段的筛选,基于提取的叶片氮含量敏感特征波段反射率,采用偏最小二乘回归算法进行叶片氮含量的估算模型构建。结果表明,利用SPA结合PLS方法所构建的叶片氮含量估算模型结构简明,有效降低了光谱波段之间的共线性,同时保证了各敏感特征波段对叶片氮含量的贡献性。所构建模型的决定系数和均方根误差分别为0.82和0.28,检验模型的相对预测偏差 (RPD) 大于2,具有较高的估算精度和良好的预测能力,可用于拔节期叶片氮含量的遥感估算。
——一种分层模拟的方法

