基于数据预处理的神经网络在船用空压机故障诊断中的应用

尚前明，曹 召，王 潇

(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)

在过去，人们针对船用空压机已发生的失效模式，仅仅局限于找到导致该故障发生的原因，从而确定应该采取哪些措施进行维修，预防故障的再次出现，这种故障发生后找故障原因的方法，只能发现故障形成的表面原因，不能分析出导致该故障所有的根本原因，对故障[1]发生的全部过程无法全部了解，很难有效地预防故障再次发生。

因此，有必要对船用空压机系统进行故障机理分析，在船用空压机的运行过程中，实时获取设备技术状态参数信息，进行相关分析，判断设备运行状态，提升船用空压机设备的安全性。BP神经网络算法在故障诊断领域发展迅速，它可以很好的拟合故障模式，并能可靠的预测故障类型。由于神经网络对整个故障数据集进行训练，模型耗时较长，影响了诊断的效率，因此文章选用PCA进行数据预处理，提取主成分，然后再进行神经网络训练，可以大大节约模型训练的时间。

1 空压机失效模式及热工参数选择

通过查阅大量相关资料，我们发现船用空压机的系统划分多种多样，而对于整个装置的失效模式分析不够到位。同时，船用空压机设备工作环境恶劣、失效模式交错复杂、失效机理藕合多变、可靠性的基础理论薄弱等特点,以及存在从事机械可靠性技术应用研究的人员相对较少，船用空压机可靠性技术缺少借鉴性等原因，造成船舶空压机的故障指标匮乏。本文以空压机典型的4种失效模式，即空压机容积流量低、空压机排气温度过高、空压机滑油变质故障及空压机不正常噪声进行分析。由于故障分析所占篇章较多，下面以空压机容积流量低为代表来分析其故障类型及故障原因见表1。

由表1可知，空压机转速、压力、温度、容积等关键参数与失效模式及故障原因存在一定的关联。因此，我们可以选用排气压力、 进气量、进气温度、冷却水温度、冷却水压力、主机转速、主机振动频率、润滑油温度、 润滑油压力和轴承温度作为热工参数来生成样本数据。

2 PCA和BP神经网络的实现

2.1 主成分分析

主成分分析[2]是通过保留原指标的主要特征，来简化数据降低维度的一种方法。空压机的热工参数有10种，所以有10个故障特征。这些故障特征之间难免有数据重叠部分，主成分分析法可以找出不相关的主要特征指标，去除数据冗余来简化数据[3]。本文通过主成分分析法对样本数据进行了标准化处理，并计算出贡献率，选择累积贡献率大于85%的特征作为主成分，求得主成分反归一化的数据作为神经网络的输入。主成分分析法的步骤如图1所示。

图1 主成分分析法一般步骤

2.2 BP神经网络理论

BP神经网络即前馈型神经网络，它是通过神经元来学习知识训练模型，并能对未知数据进行预测的一种智能算法。神经网络分为正向传播和反向传播[4]，正向传播是计算出输入X和权重W的乘积，再加上偏值b，最后通过合适的函数映射得到神经网络的输出过程，反向传播是反向逐层对成本函数进行求导，直到求出输入层变量的导数为止，然后运用梯度下降法对权值和偏值进行修正的一个过程。其单个神经元的流程示意图如图2所示。

图2 神经元流程示意图

2.3 BP神经网络结果的确定

BP神经网络[5]一般由输入层、隐含层、输出层组成。输入、输出层由一层组成，隐含层可以有多层，增加隐含层的层数会增加模型处理复杂问题的能力，但层数增多也会使模型收敛时间增加。根据反复实践，采用三层网络结构，空压机的故障诊断模型正确率较高，完全适合要求。因此，本文采用三层BP神经网络。神经网络的输入层节点数一般由样本特征数来确定，本文以主成分分析得到的特征数作为输入层的节点数，输出层一般由故障类型确定，本文共有5种故障类型，其中[1,0,0,0,0]表示空压机正常运行状态作为故障模式1；[0,1,0,0,0]表示空压机排气温度过高作为故障模式2；[0,0,1,0,0]表示空压机滑油变质故障作为故障模式3；[0,0,0,1,0]表示空压机不正常噪声作为故障模式4；[0,0,0,0,1]表示空压机容积流量低作为故障模式5。

3 算例

3.1 样本数据的确定和输入数据的处理

样本数据的选择对BP神经网络模型的建立至关重要，样本数量过少时，会使得模型故障类型欠缺，造成欠学习的现象，样本数量过多时，会使得模型计算效率下降，诊断时间过长，造成过学习的现象。所以，基于以上原因，本文选取MLG30.4/8-185G型空压机典型的30组数据作为研究对象，选用前20组样本数据作为训练数据，后10组作为测试数据集，部分数据集如表2所示。基于数据冗余的问题，我们对数据做了归一化处理，然后用主成分进行了分析。

表2中各个参数符号的物理意义：Pexh为排气压力；Vexh为进气量；Texh为进气温度；Tcw为冷却水温度；Pcw为冷却水压力；vm为主机转速；Fmh为主机振动频率；TLo为润滑油温度；PLo为润滑油压力；Tb为轴承温度。

根据累计贡献率大于等于85%的原则，我们选择了前5个特征作为主成分，其累计贡献率达到了85.628%，如表3所示。结果表明其前5个主成分包含了原始数据85.628%的信息，完全可以用来代表原始数据特征。最后把主成分分析后的前5个主成分数据乘以对应特征值的二次方根进行反归一化，得到如表4所示的数据，此数据传入神经网络的输入层。

表2 空压机样本数据

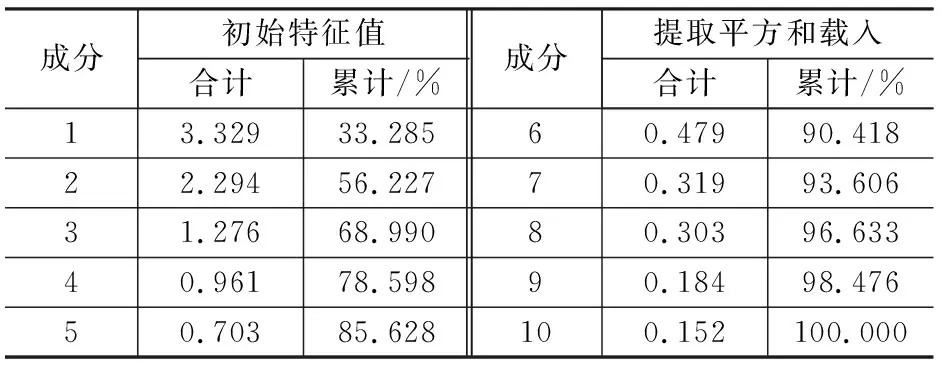
表3 总方差解释

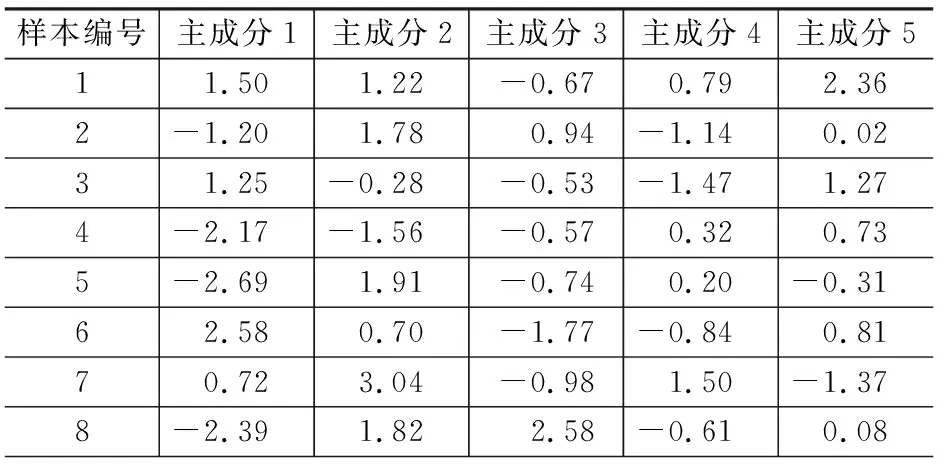
表4 主成分计算后的样本数据

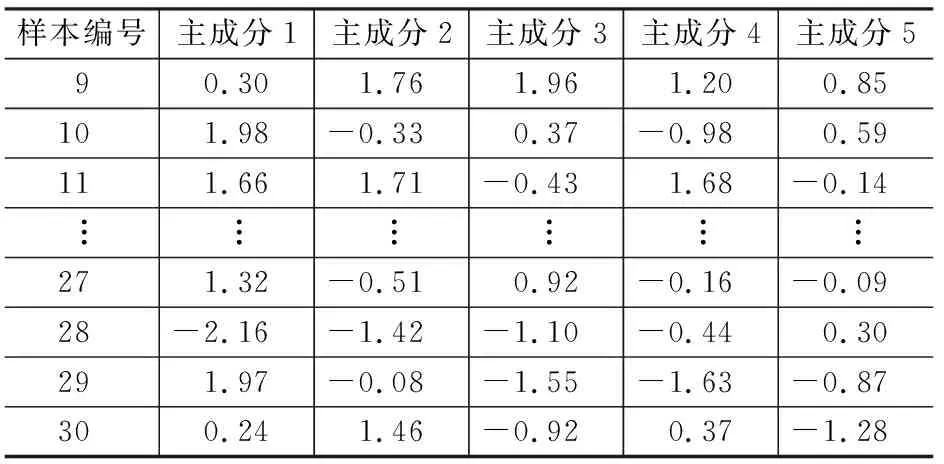
续表4 主成分计算后的样本数据

3.2 训练网络

根据分析，我们选择输入层的节点数为5个，输出层的节点数也为5个。隐含层和输出层的传递函数分别采用Tansig和Logsig，均方差目标设置为0.000 1，隐含层数初步设置为10，最后选用Trainlm函数对模型进行训练，网络训练结果如图3所示。

图3 神经网络训练结果

为了得到最佳的网络结构使模型更健壮，我们反复实验隐含层的节点数，最后得到隐含层为8时，模型精度最高，训练时间最少。至此，神经网络模型已经建立完成，需要对建立的模型进行测试。

3.3 测试网络

模型训练完成后，还需要测试模型的准确性。选择剩余的10组数据作为测试数据，对模型进行测试，结果见表5所示。

3.4 网络对比

为了更好和基于PCA数据预处理的神经网络模型对比，本文选取原始数据作为神经网络的输入数据，经过训练和测试的结果见图4所示。

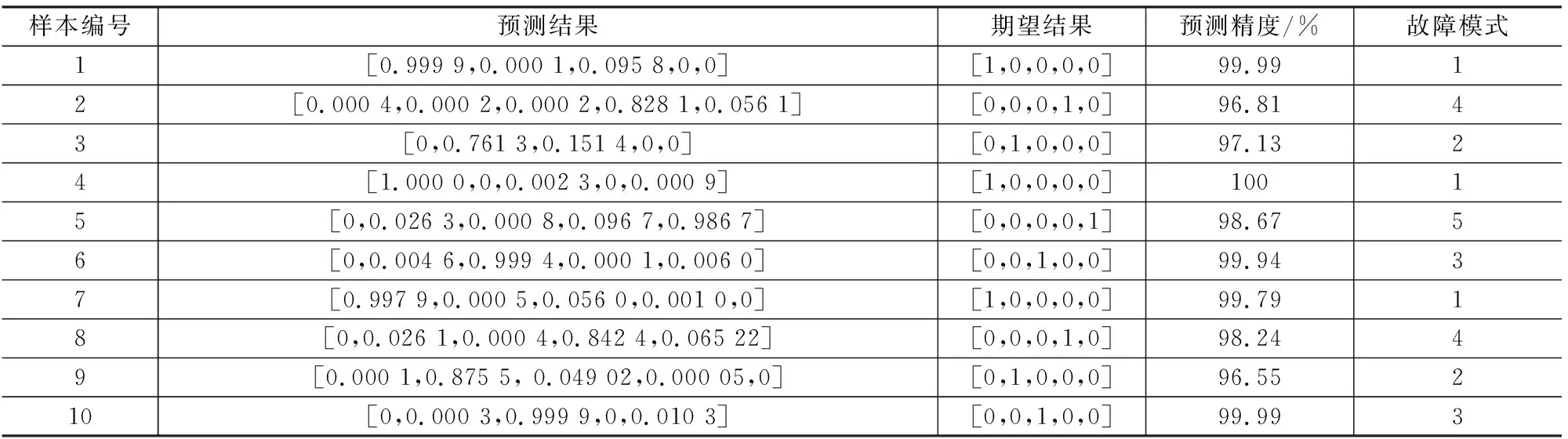
表5 神经网络测试结果

图4 未经PCA处理的神经网络训练结果

4 结束语

通过测试结果可以看出，采用基于PCA-BP神经网络的故障诊断方法可以有效的对船用空压机进行故障诊断，提高模型计算的时间。并且在现代计算机技术飞速发展的时代，可以借助编程软件，设计良好的人机界面，方便的得到诊断结果。但此、次采用的船舶空压机数据量较少，对某些故障模式可能还没有分析到，以后随着故障数据的增多会得到更加完善的网络模型。