多用型觇板研制及在全站仪检定中的应用研究

何福久,任保刚,臧炳贵

(1. 珠海市测绘院,广东 珠海 519000;2. 山东省水利勘察设计院,山东 济南 250013)

0 引 言

加常数及乘常数是测距仪主要的距离改正数之一,其测定的准确性直接影响距离测量的精度[1-4].目前,测定测距加常数及乘常数的常用方法有:解析法、迭加法、比较法、两点法、比对法、三段法、四段法等.其中六段解析法精度较高,但由于六段法需要专用的基线场地,适合于专业检定机构采用[5-6];比对法的精度高于两点法的精度,但需要具有高精度的两点间的距离,两种加常数测定方法均可达到±0.2 mm左右的测定精度[5];四段法和MetroIn工业测量系统比较法精度均优于0.3 mm,但四段法测定加常数时对基线的直线度和靶座与仪器中心同轴度要求较高,比较法则要求MetroIn工业测量系统应准确定向及精度良好[6].另外使用加常数修正野外基线测量距离后单独计算测距乘常数的方法可提高乘常数的检定精度[7-8].

针对以上方法的优缺点,本文提出了一种利用多用型觇板进行全站仪测距系统误差检测的方法.该方法适用于室内或野外短距离情况下进行全站仪测距系统误差的检测,其检定精度优于0.1 mm.多用型觇板易于制作,只需精确测定觇板中各测量标志的三维坐标后即可使用.特别适用于各测量单位日常的测距仪检定工作.

1 多用型觇板的研制

多用型觇板制作时需要满足以下几点要求:

1)觇板板体应具有一定的刚度且变形小(即觇板板体材料硬度要大、热膨胀系数要小).从而保证在搬动及温度等一些外在因素变化影响时,板体上的球形棱镜与回光反射标志之间的位置关系不发生变化;

2)觇板应尽量轻便(即应采用密度小的材料作为板体的主材料);

3)觇板上的测量标志点在纵深方向应有高低起伏;

4)多用型觇板可同时作为全站仪、电子经纬仪及数码相机的测量标靶使用.

①觇板主板体材料的选择

需要选择密度小、不易变形、膨胀系数小的材料作为觇板板材.经过分析对比不同材料的属性参数(见表1),确定选用碳纤维板作为多用型觇板主板的制作材料.

表1 各种材料的属性参数Tab.1 Properties table of diあerent types of material

②多用型觇板的制作

依据上述要求,设计的多用型觇板如图1所示.觇板安装了4个球形棱镜及数个回光反射标志及编码标志.

图1 多用型觇板Fig.1 Multipurpose measurement target vane

2 觇板中各测量标志三维坐标的精密测定

分别使用瑞士徕卡厂制造的经纬仪工业测量系统和解放军信息工程大学研制的MetroIn-DPM数字工业摄影系统[9-10]对多用型觇板的各测量标志的三维坐标进行了精密测定.表2给出了两种测量系统对回光反射标志测定的点位精度的统计结果.

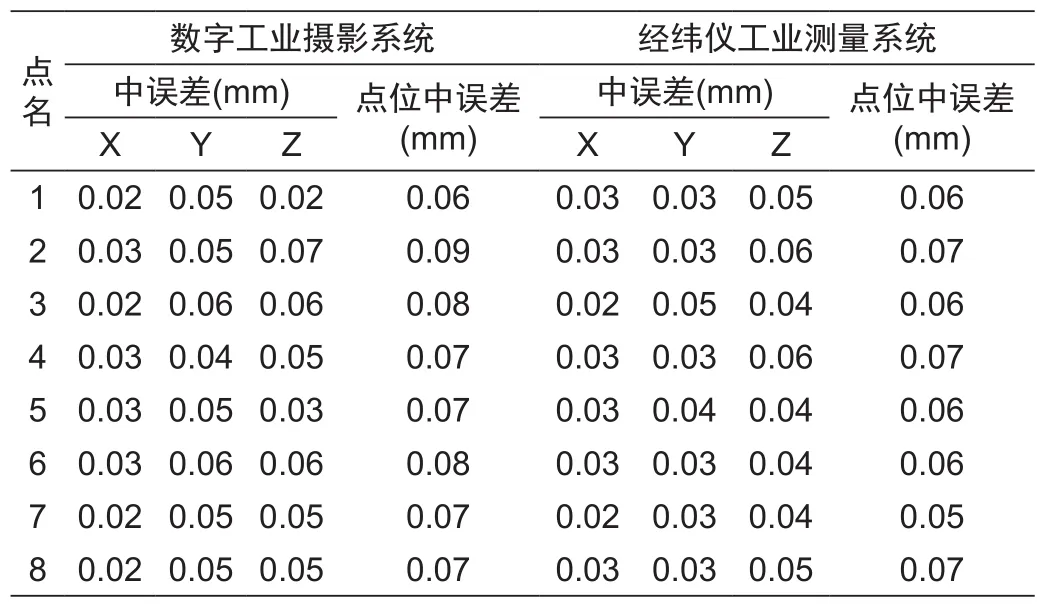
表2 两种测量系统对回光反射标志测定的点位精度统计Tab.2 Two kinds of measurement systems for measure the point accuracy of ref l ectance signal

由表2可以看出,经纬仪工业测量系统测定的各点点位中误差最大为0.07 mm,最小为0.05 mm;数字工业摄影系统测定的各点点位中误差最大为0.09 mm,最小为0.06 mm.确定取用经纬仪工业测量系统测定的觇板上各测量标志点的三维坐标作为坚强数据使用.

3 利用多用型觇板检定全站仪测距系统误差

在利用全站仪采用极坐标法进行测量时,可以通过取用多个测回的平均值减小测角及测距偶然误差的影响,但不能消除测距的系统误差.虽然测距系统误差可通过加入改正的方法进行消除,但由于在实际测量时测定气象参数的方法(一般只是在测站上测定温度、气压等)的限制及测定误差,以及仪器加常数、乘常数的变化影响,使测距的准确度降低,难以满足精密测量的需要[11-12].而采用多用型觇板可有效地减小上述系统误差的影响,提高测量的精度.现将其测量原理及方法简述如下.

坐标系转换通常由平移、旋转和尺度参数构成.设某一坐标系0-xyz先平移(x0,y0,z0),再旋转(εx,εy,εz),最后缩放k倍后,转换到另一坐标0'-x'y'z'.点P在0-xyz中的坐标为(x,y,z),在0'-x'y'z'中的坐标为(x',y',z'),则有

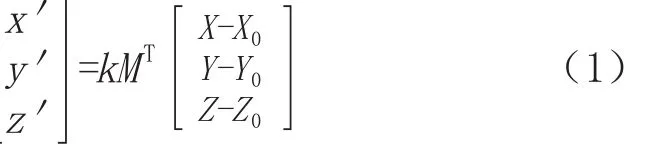
式中,k为原坐标系转换到新坐标系的尺度缩放系数,在所研究的尺度空间中可认为各向同性,故只需解算一个尺度参数.如果测量系统不存在测量误差的情况下进行坐标转换时,缩放系数K应取1.

在采用全站仪对多用型觇板各目标点的三维坐标进行测量时,虽然通过多个测回可有效地减小测角误差的影响,但测距的系统误差是不能通过多次观测消除的.由于全站仪存在测距系统误差,在依据经纬仪工业测量系统精确测定的多用型觇板各目标点的三维坐标作为基准的前提下,将导致全站仪测定的多用型觇板各目标点的三维坐标转换到经纬仪工业测量系统坐标系下时,出现k≠1的情况.

基于以上思路,采用TCA2003全站仪及多用型觇板进行了如下实验探讨:

1)首先采用经纬仪工业测量系统精确测定出多用型觇板各目标点的三维坐标;

2)在距离多用型觇板16 m处,采用TCA2003全站仪(该仪器经计量部门检定的加常数为-0.9 mm)对多用型觇板进行多次高精度测量,并将测定的各目标点的三维坐标转换到经纬仪工业测量系统标定的坐标系下.坐标转换时对缩放系数K不进行约束,得到缩放系数K1值和在X,Y,Z 3个方向的平移矢量T1值;

3)将缩放系数K约束为1,再次将TCA2003全站仪的测量数据转换到经纬仪工业系统标定的坐标系下,得出在X,Y,Z 3个方向的平移矢量T2;

4)根据两次坐标转换过程中的平移参数T1和T2,见表3,求取TCA2003全站仪对多用型觇板进行测量时的测距系统误差.

表3 约束及无约束条件下T1和T2平移矢量的对比Tab.3 The comparison between T1 and T2 translation vectors under constraints and unconstrained conditions

测距系统误差可用式(2)计算

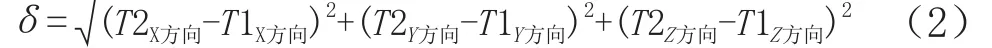
测距系统误差δ的正负号可以通过缩放系数k的变化得出,若k>1,则δ为负,若k<1,则δ为正.依据公式(2)求取的测距系统误差δ=-0.898 055 m.该误差中包含了测距仪的加常数、乘常数及气象改正.由于距离较短(16 m),因此测距仪的乘常数及气象改正影响很小,因此该值主要反映了测距仪的加常数的大小.

为验证上述思路的正确性,在测量的斜距S中人为地加入3mm误差(相当于测距仪存在3 mm的加常数),然后重新计算各目标点的三维坐标,并采用上述方法进行坐标转换.表4为加入误差后坐标转换中对K值约束与无约束两种情况下的平移矢量T1和T2的统计表.

表4 约束及无约束条件下T1和T2平移矢量对比(加入误差后)Tab.4 Comparison between T1 and T2 translational vectors in constraints and unconstrained conditions (after adding error)

由上表可知,人为加入3 mm测距误差之后,缩放系数k1=0.999 9 mm,即任意相同两点在TCA 2003全站仪坐标系下的距离大于任意相同两点在经纬仪工业系统标定坐标系下的距离.根据上面提出的理论方法,可以求算出误差δ=+2.085 350 197 mm,δ≠3 mm.出现这种现象的原因是因为实际测量中存在着δ=-0.898 055 mm的测距系统误差.因此人为加入3 mm测距误差后求取的系统误差应为:δ=2.085 350 197+0.898 055=2.983405 mm.其差值仅为0.016 95 mm.经多次测定,其中误差为0.02 mm.

由上述实验可证明,多用型觇板完全可以作为检验全站仪测距系统误差的一种工具.

为进一步验证上述方法的正确性,在实验室中选取16m的距离,对一台南方NTS352全站仪进行检测.该全站仪经计量部门检定得到的加常数为-2.1 mm.表5为南方NTS352全站仪在坐标转换中对k值约束与未约束情况下的T1和T2平移矢量的统计表.

表5 T1和T2平移矢量的对比Tab.5 The contrast between T1 and T2 translation vectors

求取的测距系统误差δ=-2.126 23 mm,实测加常数与检定值较差为0.026 mm.

4 结束语

本方法建立在自主研制的多用型觇板的基础上,可应用于全站仪测距系统误差检测工作中,特别适用于建立全局高精度控制网.但该方法不能检定测距仪的乘常数.较于其他检测方法如三段法、六段法,具有方便、灵活、高效等特点,对于测距加常数的检测精度优于0.1 mm.