自适应搜索半径蚁群动态路径规划算法

赵 峰，杨春曦，陈 飞，黄凌云，谈 诚

1.昆明理工大学 化学工程学院，昆明 650500

2.昆明理工大学 省部共建复杂有色金属资源清洁利用国家重点实验室，昆明 650093

1 引言

路径规划是指在有障碍物的已知或未知环境下，移动机器人按照一定的性能指标（如距离、时间等），搜索一条从起始位置到目标位置的最优或次优路径。考虑到移动机器人在动态复杂环境下的自主导航在无人驾驶领域有巨大的应用价值，因此该问题一直是机器人和人工智能研究领域的热点课题之一[1-3]。

蚁群算法作为仿生智能算法的一种，因其在路径规划中鲁棒性能较好、智能搜索、分布式计算和容易与其他算法相结合的优点，被广泛应用于环境部分未知或全部未知的动态路径规划中[4-5]。然而，传统的蚁群算法也存在计算时间长、收敛速度慢、易陷入局部最优解等缺陷，因此如何提高蚁群算法在动态路径规划中的收敛速度，避免局部最优值陷阱就成为一个研究热点[6-12]。基于传统蚁群算法的改进方法大致分为两类：一类是通过改进蚁群算法本身的结构和参数优化来达到目的，如最大最小蚁群系统[6]、改进距离启发因子蚁群算法[7]和角度因子蚁群算法优化等[8-9]；而另一类则是利用多种算法相结合的方法提高性能，如遗传-蚁群算法[10]、粒子群-蚁群算法[11]和模糊-蚁群算法[12-13]等。在第一类方法中，最大最小蚁群系统算法用于防止算法过早收敛于局部最优解问题；文献[7]通过改进距离启发因子来增加目标节点对下一节点的影响，从而避免陷于局部最优解，提高收敛速度；文献[8-9]结合具体的应用领域约束，基于蚁群算法综合考虑节能、能量均匀分布、路径距离等指标下的路径规划问题。而在第二类方法中，主要是利用不同智能算法的互补性，达到提高性能的目的。其中遗传-蚁群算法的结合是利用遗传算法的快速全局搜索能力和蚁群算法的并行、全局收敛能力，形成一种快速性和全局收敛性良好的混合算法；而粒子群-蚁群算法则是利用粒子群算法对蚁群算法的适配参数进行优化，提高其全局寻优效率；模糊-蚁群算法主要是利用模糊规则实现组合算法在环境未知情况下进行路径规划的自适应能力，增加其实用性。虽然组合算法的优化效率、收敛速度都有较大提高，但其算法计算量较大，对移动机器人性能要求较高。

上述改进的蚁群算法虽然不同程度地减少了计算时间，提高了搜索效率和收敛速度，但没有综合考虑在搜索范围有限、实时性要求较高和移动机器人计算能力有限的情况下进行动态路径规划的问题 。为此，这里设计了一种能在实时性要求内，根据障碍物多少进行搜索半径自动调整的自适应搜索半径蚁群动态路径规划算法（SRL-ACA）。该算法首先按照实时性要求把整个路径规划区域分割成若干个子区域，则子区域的边界即为实时性要求的上限；然后借鉴滚动窗口法[14-15]思想设计了一种局部搜索半径法来描述移动机器人环境探索能力有限这一约束，并通过把局部搜索半径设计成为可以根据环境复杂程度进行自适应调整的方式达到充分利用移动机器人有限的计算能力之目的；最后构造了一种随机轮盘赌方法来选择局部目标点，使得该算法在提高收敛速度的同时，有效降低了陷入局部最优的概率。通过3种方法的综合使用，使得该算法具有在实时性需求较高、未知环境复杂和计算能力有限3个约束条件下进行动态路径规划的能力。此外，仿真实验表明该算法在路径距离优化、收敛时间优化和动态复杂环境自适应能力方面均具有较好的综合性能。

2 问题描述与建模

2.1 环境建模

为不失一般性，这里采用主流的栅格法来对搜索环境进行建模。即记G为移动机器人在二维平面内的运动区域，区域内的栅格编号如图1所示，在G中建立直角坐标系，以G左下角为坐标零点，横轴为X轴，纵轴为Y轴。设在相关区域内存在若干个障碍物栅格，在图1中用黑色栅格表示，无障碍物栅格则用白色栅格表示。假设移动机器人能够从起始位置经过路径规划最终达到目的位置，机器人只在各个栅格内的中心点行走，则机器人位置的计算公式为分别为式（1）和式（2）：

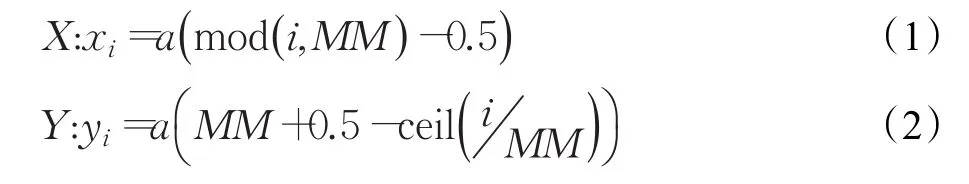
其中，a为每个栅格的边长，横（纵）坐标的最大栅格数值为MM，栅格总数为e=MM⋅MM，每个栅格的坐标为，i为每个小正方形的栅格编号，mod为求余运算，而ceil为舍余取整运算。这里假定移动机器人的起始位置和最终目的位置已知。

在动态路径规划的研究中，通常是以移动机器人为运动载体，而把局部规划过程中从局部出发点至局部最优点之间的距离叫做搜索半径。定半径指在一次完整的路径规划过程中，每次搜索半径的长度保持不变，其思想与滚动窗口法相似。该搜索半径的取值与环境的实时性成反比，即动态规划要求的实时性越强，则搜索半径越短。为便于比较，用n步搜索半径来描述一次局部路径规划所能覆盖的范围。当移动机器人采用自适应搜索半径算法时，n可以取子区域内任意有限值；当移动机器人采用固定搜索半径算法时，n则为一个固定值。

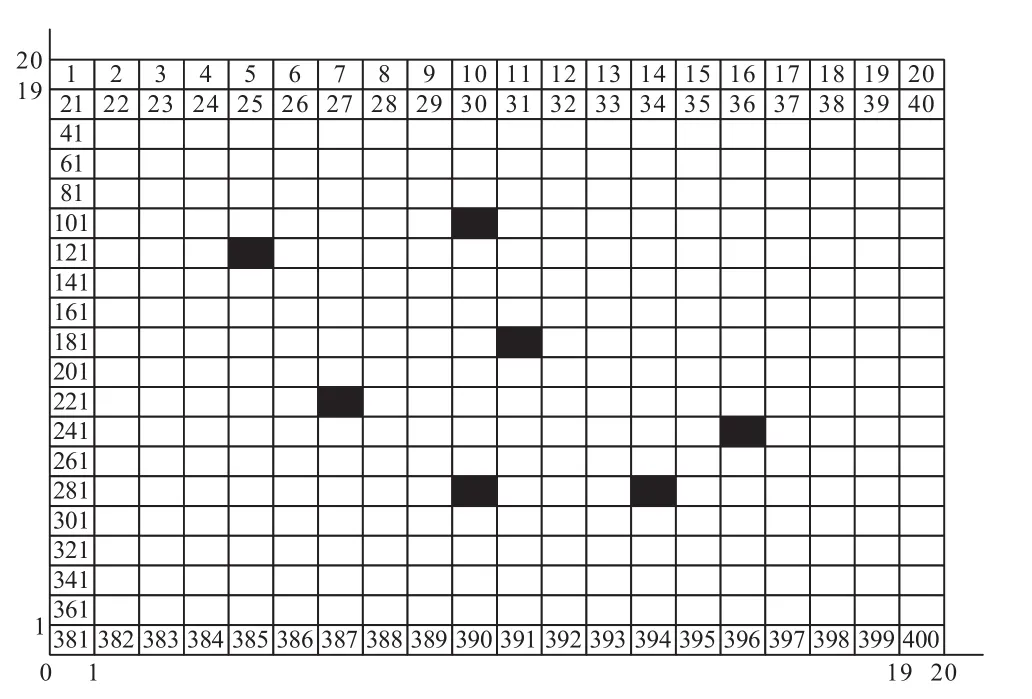
图1 栅格法构建环境示意图

2.2 动态障碍变化设置

为比较不同方法在未知障碍环境下进行动态路径规划时的特点，这里设计了一种以时间为变换指标的动态障碍变化规则，即以移动机器人所行走的次数来触发环境中障碍分布的变化。例如3次动态障碍变化规则为移动机器人的行走次数为3的整数倍时进行障碍场景变化，其他次数时障碍场景保持不变。因此，当移动机器人在一个变化周期内行走时，该子区域的障碍分布是固定不变的，移动机器人所在子区域外的障碍分布与本次路径规划无关。此外，移动机器人行走次数与实时性密切相关，即设定的次数越少，实时性越强，全局动态障碍环境变化的总次数越多，要求算法对动态路径障碍变化的适应能力越强。

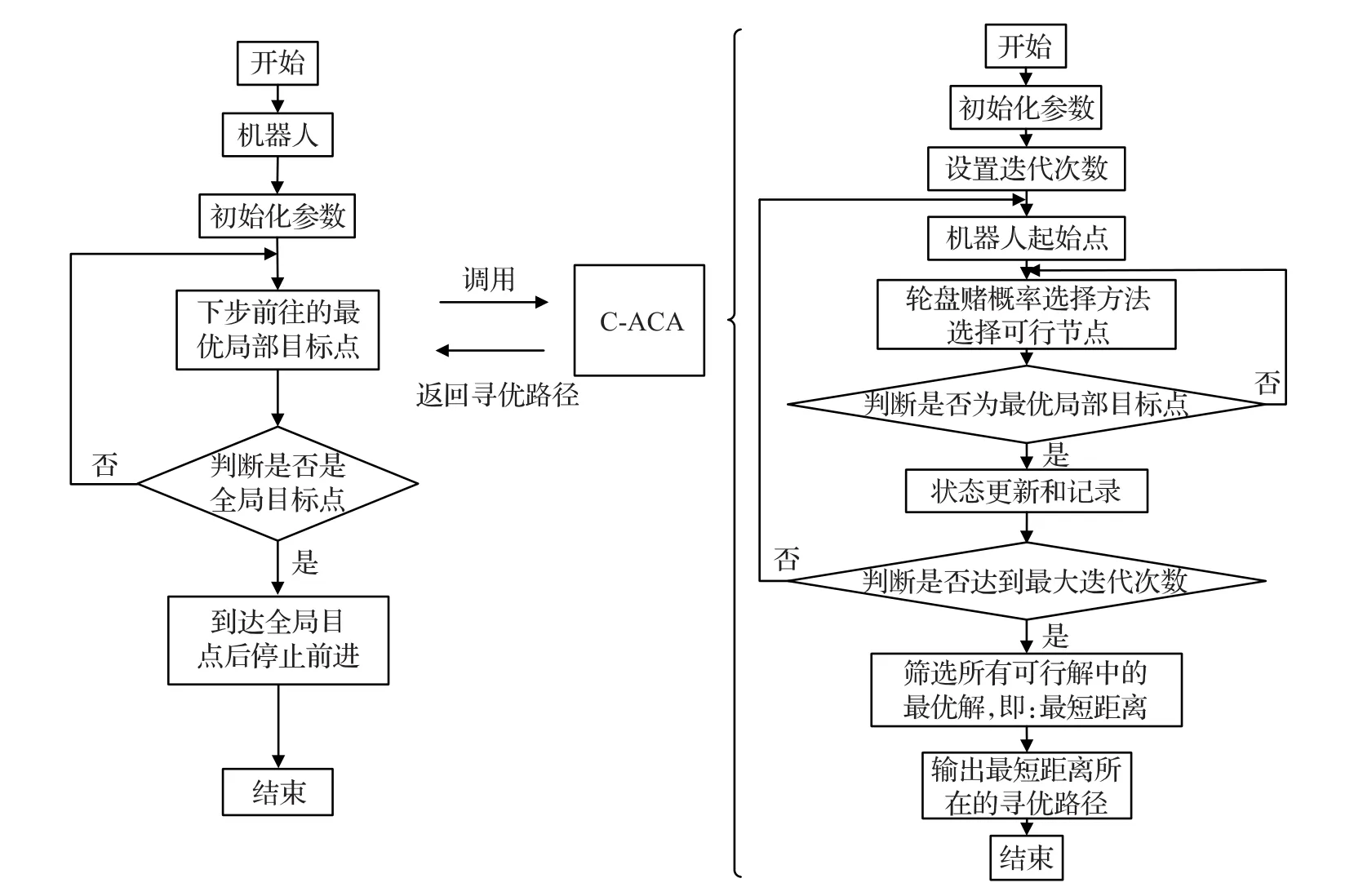
图2 边寻边走策略流程图

3 蚁群算法的改进

3.1 边寻边走策略

由于在未知环境中进行路径规划，每次局部动态路径规划均需要调用改进的蚁群算法，因此这里采用边寻边走的策略用于局部信息获取，具体策略如图2所示。

在该算法中，移动机器人首先要找到最优局部目标点，然后利用可调用蚁群算法（Called Ant Colony Algorithm，C-ACA）寻找到达该最优局部目标点的最佳路径并行走。当机器人到达最优局部目标点后，需要判断该局部目标点是否为全局目标点，若是则整个动态路径规划结束；若不是全局目标点，则返回寻找下一个搜索半径内的最优局部目标点，然后重复上一个循环，直到找到全局目标点为止。因为局部路径优化仅在较小范围中进行，所以蚁群算法的蚂蚁个数和迭代次数均可以大大减少，从而节约了规划时间。

3.2 最优局部目标点的选择

考虑到SRL-ACA算法在动态路径寻优过程中，最优局部目标点的选取方法在很大程度上决定了该算法能否避免陷入局部最优解，找到有效最优路径。因此，这里采用了随机轮盘赌算法（Stochastic Roulette Algorithm，SRA）来确定最优局部目标点。

轮盘赌策略[16]的核心思想是根据不同选项的可能性分配相应的被选择概率大小，确保大概率选项有大的被选择概率的同时，保留其他具有相对较低概率的选项也有被选择的可能。这种算法可以避免局部最优陷阱，缺点是收敛速度较慢。为此，这里提出了一种具有较快收敛速度的随机轮盘赌算法，具体策略如图3所示。

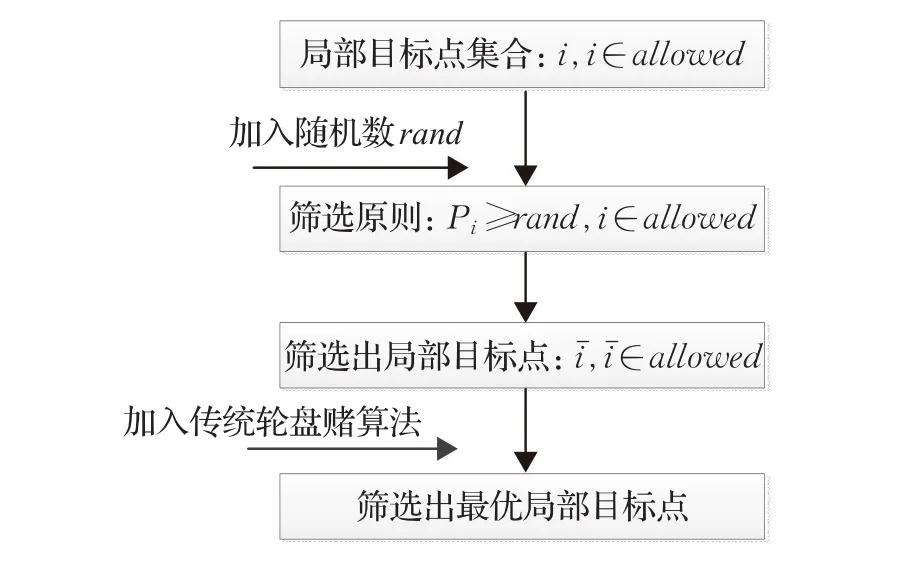
图3 随机轮盘赌算法流程图

首先确定局部目标点i，i∈allowed，其中allowed为本次搜索半径内，排除已经走过的栅格后可以到达的所有非障碍栅格的集合。随后通过加入一个服从均匀分布的随机数作比较，筛选出集合中被选择概率Pi大于等于rand的局部目标点i的集合，最后调入传统轮盘赌算法筛选出最优局部目标点。

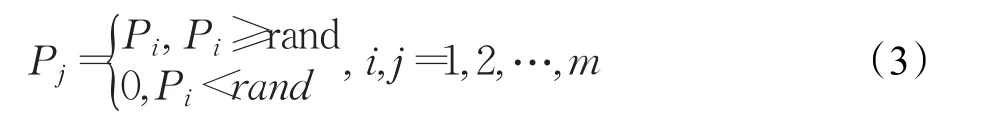
注意1随机轮盘赌算法实际上是基于传统轮盘赌算法和贪婪算法的一种改良算法，既能够提高传统轮盘赌算法的收敛速度，又能够避免贪婪算法容易陷入局部最优值的缺陷。当随机数rand=0时，该算法等效于传统轮盘赌算法，能够避免局部最优值陷阱；而当rand=max(Pi)时，则该算法相当于贪婪算法，具有较快的收敛速度。

4 自适应搜索半径路径规划方法

4.1 局部搜索半径的选择

在SRL-ACA算法中，一个关键问题是选择合适的搜索半径，以获得计算能力、寻优时间和寻优距离3个指标的综合优化效果。因此，这里设计了一个有效的搜索半径选择原则，具体方案如图4所示。

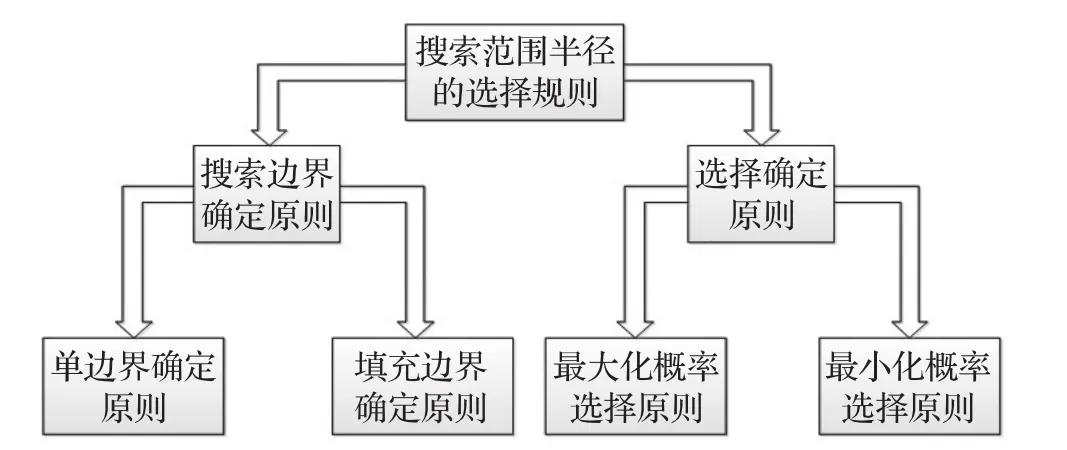
图4 搜索范围半径的选择规则确定流程图

由图4可知，搜索半径的选择规则共分为两个步骤：第一步是设计搜索边界确定原则；第二步是设计选择确定原则。在两步设计原则选取完成后，搜索半径将最终被确定。

在边界确定原则中，这里设计了两种确定原则，即单边界确定原则和填充边界确定原则。其中单边界确定原则是以移动机器人位置为中心，相同步长的搜索半径能到达的方格组成的闭合边界中，无障碍栅格占边界总格数的比例来进行判断；而填充边界确定原则是利用搜索半径能够覆盖的范围中，无障碍栅格占所覆盖范围总格数的比例来进行判断。即令变量R=1,2,…,n为搜索半径，n为搜索半径最大步长，则单边界确定原则中栅格总数为Sd=8R，而填充确定原则中的栅格总数为St=(2R+1)2。

在第一步搜索边界确定原则完成后，再进行第二步选择确定原则。这里也设计了两种选择确定原则：最大化概率选择原则和最小化概率选择原则。最大化概率选择原则为：比较在不同搜索半径下所包含的总栅格中，选择无障碍栅格占比最大值所对应的搜索半径为本次局部路径规划搜索半径；反之，则为最小化概率选择原则。即令分别为搜索半径为 R的单边界和填充边界无障碍栅格总数，则相应的最大化概率选择原则为：

而最小化概率选择原则为：

两种确定原则的2步、4步实例分别如图5、图6所示。图5中，红色正方形栅格为机器人的当前位置，由内到外的两个橙色矩形所包括的区域分别为两步搜索半径和4步搜索半径所覆盖的区域，两个蓝色矩形经过的栅格分别为相应搜索半径所对应的边界栅格。在单边界确定原则下，第2步搜索半径的总栅格数为16格，4步为32格，相应的占比分别为0.625和0.718。按照最大化概率选择原则应选择4步搜索半径；而按照最小化概率原则应选择2步搜索半径。

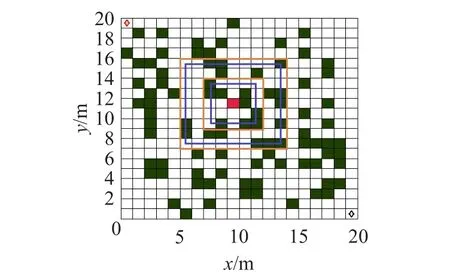
图5 单边界确定原则原理图

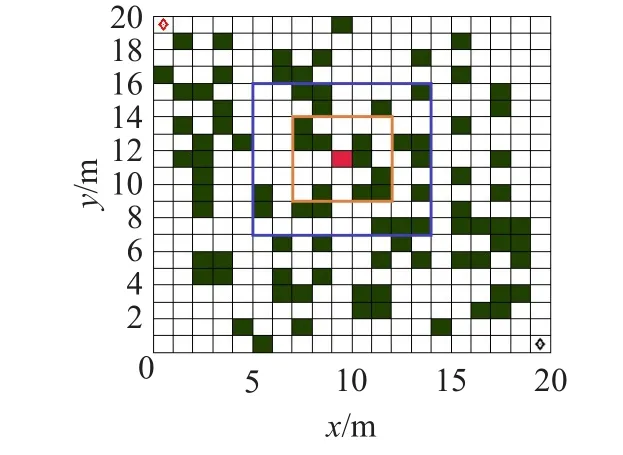
图6 填充边界确定原则原理图

同理，图6中的红色正方形栅格为机器人的当前位置，橙色矩形与蓝色矩形分别为两步搜索半径和4步搜索半径所覆盖的区域。在填充边界确定原则下，2步搜索半径的总栅格数为25格，4步为81格，相应的占比分别为0.640和0.641，按照最大化概率选择原则应选择4步搜索半径，而最小化概率原则应选择2步搜索半径。

4.2 自适应搜索半径蚁群动态路径规划算法的步骤

综上所述，移动机器人自适应搜索半径蚁群动态路径规划算法具体分为下面5个步骤。

（1）根据规划实时性要求确定本次动态路径规划的搜索半径上界，即移动机器人在一次局部动态路径规划中所允许行走的最大步数。

（2）移动机器人以当前位置为出发点，采用搜索半径的选择规则确定本次局部动态路径规划的搜索半径值。

（3）调用随机轮盘赌方法确定本次动态路径规划的最优局部目标点。

（4）调用C-ACA算法规划出本次局部优化路径。

（5）通过计算本次最优局部目标点与终点的二范数是否为零来判断该节点是否为终点。如果是终点则本次路径规划完成，反之则返回第（2）步。

通过上述5个步骤的不断循环，即可实现全局的动态路径规划。

5 仿真实验与分析

为了突出SRL-ACA算法的特点，令该算法中搜索半径为固定值，并称该算法为固定搜索半径蚁群动态路径规划算法（FRL-ACA）。同时，把这两种算法应用于同等环境下的路径寻优的问题。

所有算法程序均采用MATLAB语言进行编程，障碍变化规则为时间变换规则，路径规划范围为20×20的栅格面积，算法的各参数参见文献[17]，初始值设置如表1和表2所示。

表1 两种算法的公共参数设置

表2 各算法的自有参数设置

5.1 动态性能比较

首先采用SRL-ACA算法（1～4步自适应搜索半径）和FRL-ACA算法（1步搜索半径）进行动态路径规划的仿真结果如图7所示。在本次仿真规划过程中共有5个障碍变化场景，如图8～12所示。其中前4个障碍场景每3次规划后变化1次，12次之后均采用图12的障碍场景。5个障碍场景图中的方框表示在该障碍场景下移动机器人一次路径规划走过的范围。

由图7可知，两种算法均很好地适应障碍变化，各自规划出一条从出发点到终点的优化路径。相对而言，SRL-ACA算法的路径要更短些。从图8～12中画出的一次规划的路径曲线可以看出，这些路径均是可行的。其中图8、图12为2步半径，图9为4步半径，图10、图11为1步半径。

5.2 搜索半径选择规则对优化参数的影响

为了测试所设计算法对环境变化的自适应能力，在这里通过设置相同的算法参数和环境参数，来比较SRL-ACA算法和FRL-ACA算法在路径寻优关键参数上的差异。为确保寻优关键参数的有效性，这里的最优路径长和最短时间均是50次寻优结果的平均值。

首先，考虑栅格确定规则为填充边界确定原则，搜索半径确定原则为最大化概率选择原则时两种算法的性能比较。设SRL-ACA算法的搜索半径变化范围为1～2步，FRL-ACA算法的搜索半径固定为1步，则具体仿真结果如表3所示。

图7 动态路径寻优对比图

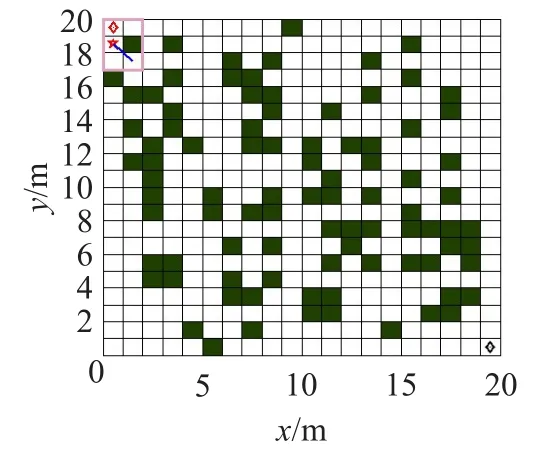
图8 G1寻优环境栅格图

图9 G2寻优环境栅格图

图10 G3寻优环境栅格图

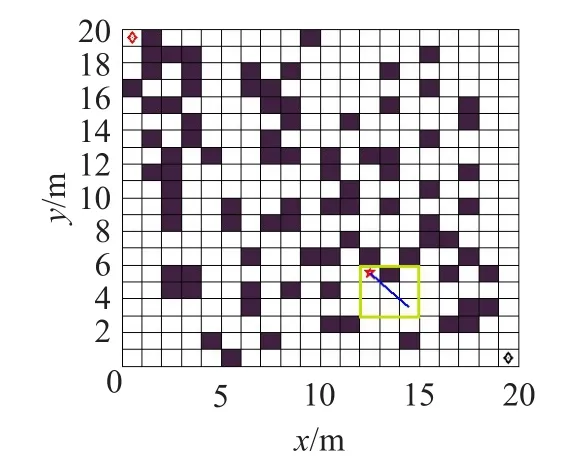
图11 G4寻优环境栅格图

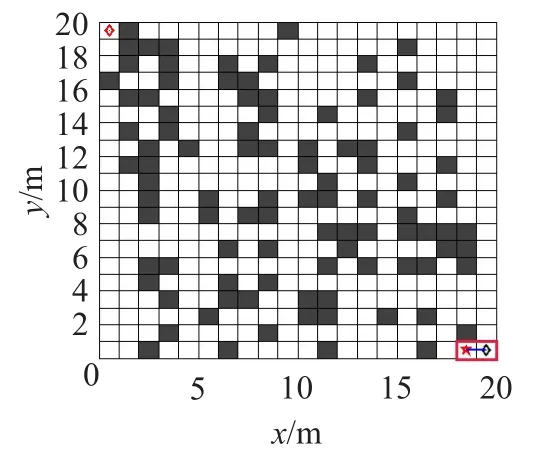
图12 G5寻优环境栅格图

表3 FRL-ACA和SRL-ACA算法路径寻优参数表

由表3可知，SRL-ACA算法的最优路径和寻优时间两项关键指标上相对于FRL-ACA算法都有明显改善和提高，表明自适应搜索半径算法有较好的动态路径规划性能。

其次，考虑栅格确定规则为单边界确定原则，搜索半径确定原则为最大化概率选择原则时两种算法的性能比较。设SRL-ACA算法的搜索半径变化范围为1～3步，而FRL-ACA算法的搜索半径分别固定为1～3步。此外，为测试算法对障碍变化的适应能力，这里按照障碍个数从少到多的顺序给出5个静态障碍场景，具体性能指标如表4所示。

表4 FRL-ACA和SRL-ACA算法路径寻优参数表

由表4可知，SRL-ACA算法在障碍较少的场景①和②具有最短的路径距离，而在其他的场景中也具有较短的路径距离，说明该算法对障碍环境变化具有较强的适应性。

再次，考虑在同等条件下SRL-ACA算法分别采用单边界确定原则和填充边界确定原则时的性能差异，具体如表5所示。

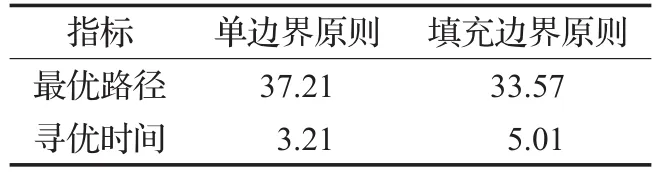
表5 SRL-ACA算法路径寻优参数表

由表5可知，在最优路径指标上填充边界确定原则优于单边界确定原则，而在寻优时间指标上则是单边界确定原则强于填充边界确定原则，可以具体要求选择其中一种。

最后，为了比较最大化概率选择原则和最小化概率选择原则对动态路径规划性能参数的影响，这里采用SRL-ACA算法分别在两种选择原则下进行仿真实验。为体现差异性，这里的栅格面积取50×50，具体结果如表6所示。

表6 SRL-ACA算法路径寻优参数表

由表6的对比结果可知，最大化概率选择原则在最优路径和寻优时间两项关键指标方面都明显优于最小化概率选择原则，说明基于最大化概率选择原则时SRL-ACA算法更具优势。

6 结束语

考虑在全未知复杂动态环境进行动态路径规划的过程中，存在的规划实时性要求高，移动机器人的计算能力和搜索半径有限，规划路径距离和算法收敛时间之间无法兼顾等问题，基于改进蚁群算法构建了一种新型的搜索半径自适应蚁群动态路径规划算法。仿真实验表明，该算法能够在确保实时性要求的前提下，通过自适应调整搜索半径，使得移动机器人的计算能力始终得到充分的利用，从而进一步缩短路径距离，减少收敛时间，实现对复杂未知环境的有效动态路径规划。